






茨城県の2023年3月実施の令和5年度(2023年度)入学者の公立高校入試問題の解説をしています。
受験勉強において、過去問を解くことはとても効果的な勉強法です。ぜひ、受験までに一度挑戦し、問題の傾向を掴んでおきましょう。合わせて、対策などをたてられるととても良いですね。
また、過去問で苦手な点が見つかった場合は、そこを中心に試験日当日までにしっかりと対策しておきましょう。
(1)次の①~④の計算をしなさい。
①$1-6$
②$2(x+3y)-(5x-4y)$
③$15a^2b \div 3ab^2 \times b^2$
④$\frac{9}{\sqrt{3}}-\sqrt{12}$
(2)$x^2-6x+9$を因数分解しなさい。
(1)次の①~④の計算をしなさい。
① \(1-6 = -5\)
② \(2(x+3y)-(5x-4y) = 2x+6y-5x+4y = -3x+10y\)
③ \(15a^{2}b \div 3ab^{3} \times b^{2} = 15a^{2}b^{3} \div 3ab^{3} = 5a\)
④ $$ \frac{9}{\sqrt{3}} – \sqrt{12} $$ $$ = \frac{9}{\sqrt{3}} – \frac{\sqrt{36}}{\sqrt{3}} $$ $$ = \frac{9-6}{\sqrt{3}} $$ $$ = \frac{3}{\sqrt{3}} $$ $$ = \sqrt{3} $$
(2)$x^2-6x+9$を因数分解しなさい。
$(x − 3)^2$
足して-6、かけて9になる 2 つの数の組み合わせを考えればよい。
かけて9になる2つの数の組み合わせは(1,9)(-1,-9)(3,3)(-3,-3)の 4 つ。
この中で足して-6 になるのは(-3,-3)。
次の(1)~(4)の問いに答えなさい。
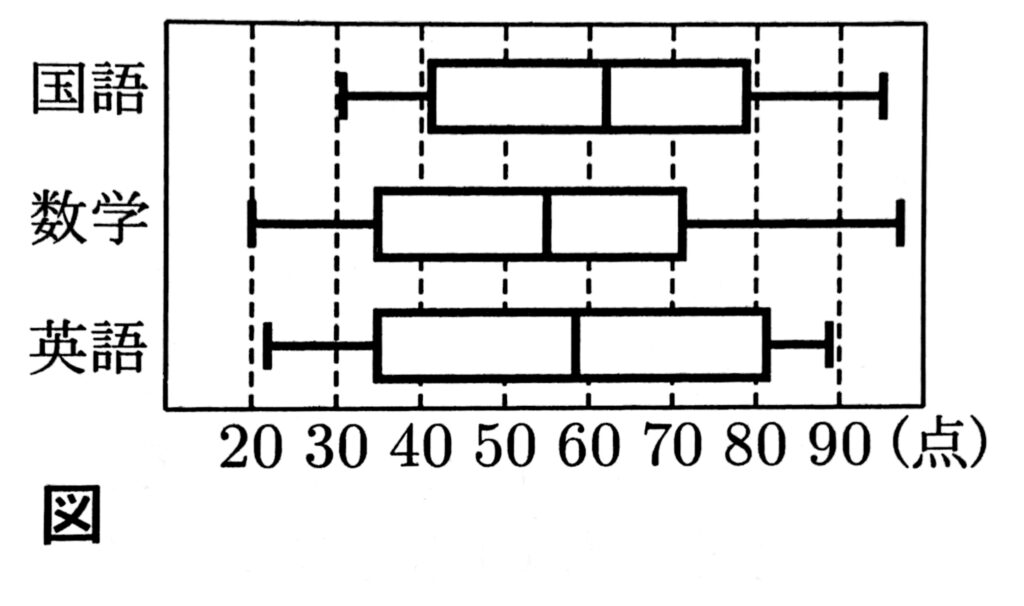
(1)次の図は、ある中学校の3年生25人が受けた国語、数学、英語のテストの得点のデータを箱ひげ図で表したものである。
このとき、これらの箱ひげ図から読み取れることとして正しく説明しているものを、次のア~エの中から2つ選んで、その記号を書きなさい。
ア 3教科の中で国語の平均点が一番高い。
イ 3教科の合計点が60点以下の生徒はいない。
ウ 13人以上の生徒が60点以上の教科はない。
エ 英語で80点以上の生徒は6人以上いる。
(2)$\frac{252}{n}$の値が、ある自然数の2乗となるような、最も小さい自然数$n$の値を求めなさい。
(3)$x$についての2次方程式
$x^2+3ax+a^2-7=0$がある。$a=-1$のとき、この2次方程式を解きなさい。
(4)チョコレート何個かと、それを入れるための箱が何個かある。1個の箱にチョコレートを30個ずついれたところ、すべての箱にチョコレートを入れてもチョコレートは22個余った。そこで、1個の箱にチョコレートを35個ずつ入れていったところ、最後の箱はチョコレートが32個になった。
このとき、箱の個数を求めなさい。
(1)イ、エ
ア:箱ひげ図には平均値は記されていない。
イ:各図の左端の縦線がその教科での最低点を表している。どの教科でも20点以上であるので、この3つを足し合わせたら確実に60点を超えるため、合計点が60点以下の生徒はいないことが分かる。
ウ:中学三年生の中での中央値は12位の人と13位の人の間の点数である。つまり、中央値より多い点数を取った人は12人である。国語を見ると、中央値が60点を上回っているので、12人以上いるということは分かるが、もう一人60点を超えている人がいるかは分からない。
エ:各箱の右の線は第3四分位数を表している。第3四分位数はデータを小さい順番に並べたときの、全体の3/4番目のデータである。つまり、第3四分位数を超えている人は全体の1/4の6人である。英語を見ると、第3四分位数が80点であるため、80点を超えている人が6人いるということになる。
(2)7
252を素因数分解すると、$2^2×3^2×7$となる。つまり、252を7で割ると$2^2×3^2$となり、これは$6^2$となる。
(4) 5個
2つの状況が示されているので、2つの式を作るとよい。
箱の数を\(x\)、チョコレートの数を\(y\)とおく。
問題文から式を作ると、
y = 30x+22 ・・・①
y = 35(x-1)+31 ②
=35x-3・・・②
xを求めたいので、yを消去すると、
30x+22=35x−3
−5x=−25
x=5
つまり、箱は5個。
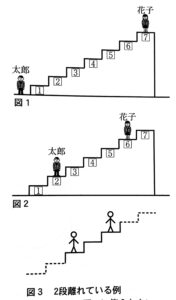
下の図1のように1⃣から7⃣までの番号の書かれた階段がある。地面の位置に太郎さん、7⃣の段の位置に花子さんがいる。太郎さん、花子さんがそれぞれさいころを1回ずつ振り、自分が出した目の数だけ、太郎さんは1⃣、2⃣、3⃣、…と階段を上り、花子さんは6⃣、5⃣、4⃣、…と階段を下りる。例えば、太郎さんが2の目を出し、花子さんが1の目を出したときは、下の図2のようになる。また、2段離れているとは、例えば、図3のような状態のこととする。
このとき、次の(1)~(3)の問いに答えなさい。
ただし、さいころは各面に1から6までの目が1つずつかかれており、どの目が出ることも同様に確からしいとする。
(1)太郎さんと花子さんが同じ段にいる確率を求めなさい。
(2)太郎さんと花子さんが2段離れている確率を求めなさい。
(3)太郎さんと花子さんが3段以上離れている確率を求めなさい。
(2) \(\frac{2}{9}\)
2人が2段離れているパターンは、(太郎の目,花子の目) = (1,4)(2,3)(3,2)(4,1)(3,6)(4,5)(5,4)(6,3) の8パターン。
全体のパターンは(1)と同じなので、求める確率は \(\frac{8}{36}=\frac{2}{9}\)。
(3) \(\frac{1}{3}\)
3段以上離れているということは、全体から同じ段でいるパターン、1段離れているパターン、2段離れているパターンを引いた場合ということ。
このうち、1段離れているパターンだけ求めていないのでそれを求める。
2人が1段離れているパターンは、(太郎の目,花子の目) = (1,5)(2,4)(3,3)(4,2)(5,1)(2,6)(3,5)(4,4)(5,3)(6,2) の10パターン。
つまり、\(36-6-8-10=12\)
求める確率は \(\frac{12}{36}=\frac{1}{3}\)。
次の図1のように、タブレット端末の画面に長さが14cmの線分ABを直径とする円Oが表示されている。さらに、円Oの円周上の2点A,Bと異なる点C、点Aにおける円Oの接線l、l上の点Pが表示されている。点Pはl上を動かすことができ、太郎さんと花子さんは、点Pを動かしながら、図形の性質や関係について調べている。
このとき、次の(1)(2)の問いに答えなさい。
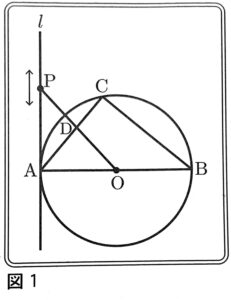
(1)太郎さんは線分OPと線分BCが平行になるように点Pを動かした。
①線分ACと線分OPの交点をDとし、BC=10cmとするとき、線分ODの長さを求めなさい。
②太郎さんは、△ABC∽△POAであることに気づき、次のように証明した。【ア】~【オ】をうめて、証明を完成させなさい。
<証明>
△ABCと△POAにおいて
【ア】だから、【イ】=90°…①
直線lは点Aにおける円Oの接線だから
∠PAO=90°…②
①、②より、【イ】=∠PAO…③
平行線の同位角は等しいから、【ウ】=【エ】…④
③、④より、【オ】がそれぞれ等しいので、△ABC∽△POA
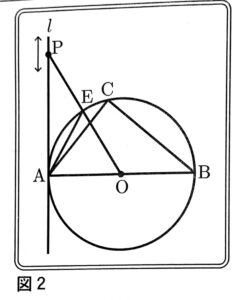
(2)花子さんは次の図2のように∠AOP=60°となるように点Pを動かした。線分OPと円Oとの交点をEとするとき、△APEの面積を求めなさい。
(1)
① 中天連結定理の逆(三角形の底辺を除く一辺の中点から、底辺の平行線を引くと、残りの辺の中点を通る)を用いる。ODはABの中点Oを通り、ACに向かって引かれた底辺CBの平行線であるので、DはACの中点。中天連結定理より、ODはBCの半分の長さなのでOD=5㎝。
②
ア、イ:△ABCと△POAのうち、∠PAO=90°であると書かれているため、∠PAOに対応する△ABCにおける角は、∠ACB。つまりイは∠ACB。∠ACB=90°である理由は、円周角の定理により、半円の弧に対する円周角だからだ。
ウ、エ:二つの三角形のうち、同位角の関係にあるのは∠AOPと∠CBA。
オ:2組の角が等しければ相似である。
O(0,0)A(6,0)B(6,6)とするとき、次の(1)(2)の問いに答えなさい。
次の図1において、mは関数$y=ax^2(a>0)$のグラフを表し、C(2,2)D(4,4)とする。
①mが点Bを通るとき、aの値を求めなさい。
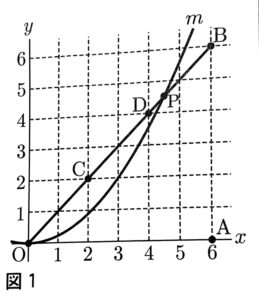
②次の文章の【Ⅰ】~【Ⅲ】に当てはまる語句の組み合わせを、下のア~カの中から1つ選んで、その記号を書きなさい。
mと線分OBとの交点のうち、点Oと異なる点をPとする。はじめ、点Pは点Dの位置にある。
ここで、aの値を大きくしていくと、点Pは【Ⅰ】の方に動き、小さくしていくと、点Pは【Ⅱ】の方に動く。
また、aの値を$\frac{1}{3}$とすると、点Pは【Ⅲ】上にある。
ア Ⅰ:点B Ⅱ:点C Ⅲ:線分OC
イ Ⅰ:点B Ⅱ:点C Ⅲ:線分CD
ウ Ⅰ:点B Ⅱ:点C Ⅲ:線分DB
エ Ⅰ:点C Ⅱ:点B Ⅲ:線分OC
オ Ⅰ:点C Ⅱ:点B Ⅲ:線分CD
カ Ⅰ:点C Ⅱ:点B Ⅲ:線分DB
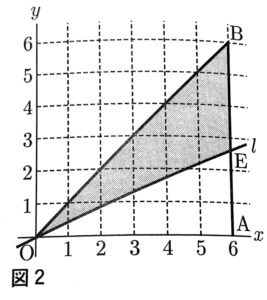
(2)次の図2で、$y=bx$で表される直線lと2点A,Bを除いた線分ABが交わるとき、その交点をEとする。
このとき、次の[条件1]と[条件2]の両方を満たす点の個数が12個になるのは、bがどのような値のときか。bのとりうる値の範囲を、不等号を使った式で表しなさい。
[条件1]x座標もy座標も整数である。
[条件2]△OEBの辺上または内部にある。
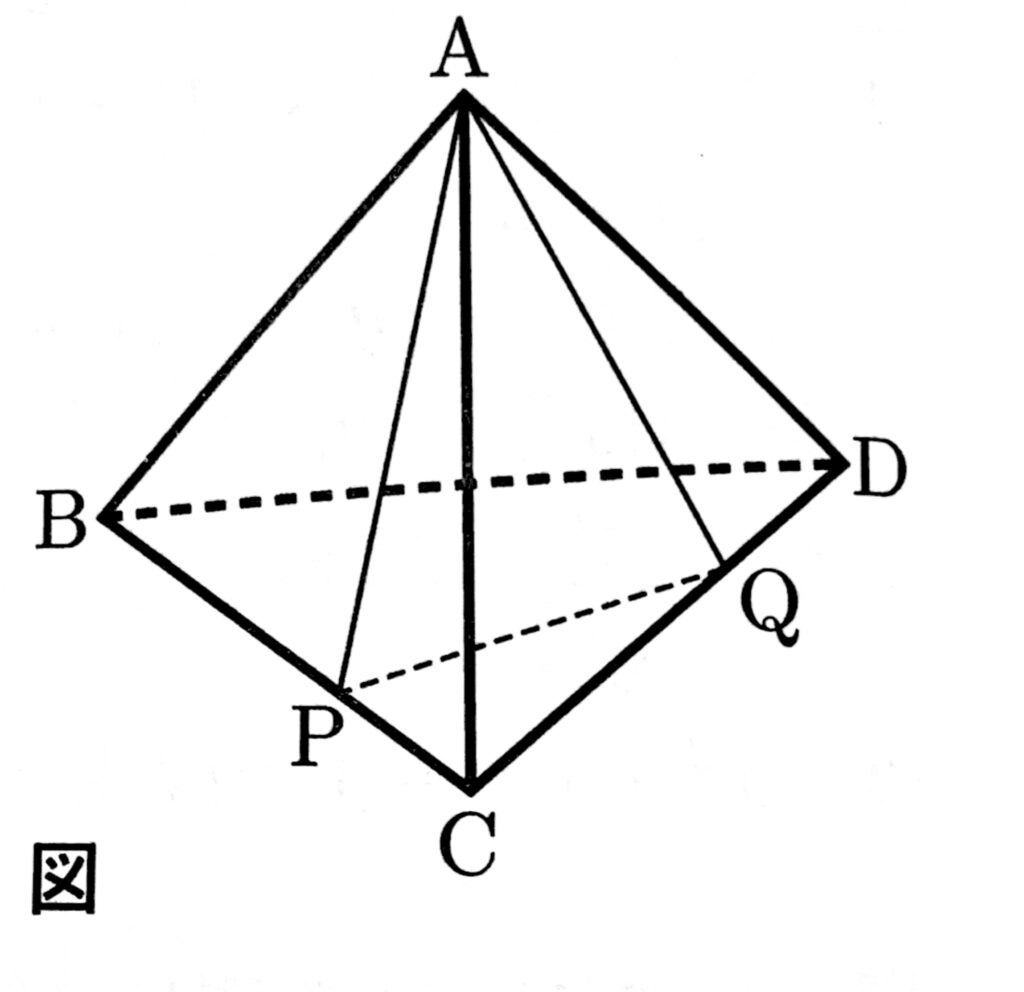
次の図のような、1辺が6cmの正四面体がある。辺BC上にBP:PC=2:1となる点P、辺CD上にCQ:QD=2:1となる点Qをとる。
このとき、次の(1)(2)の問いに答えなさい。
(1)△CPQはどんな三角形か。
最も適切なものを、次のア~エの中から1つ選んで、その記号を書きなさい。
ア 正三角形
イ 二等辺三角形
ウ 直角三角形
エ 直角二等辺三角形
(2)
①線分AQの長さを求めなさい。
②直線APを軸として、△APQを1回転させてできる立体の体積を求めなさい。ただし、円周率はπとする。
家庭教師のやる気アシストは、茨城県にお住まいの受験生のお子さんを毎年たくさん指導をさせ頂き、合格に導いています。
高い合格率の秘訣は、指導経験豊富な先生の指導力に加え、1対1の指導でお子さん一人ひとりの状況に合わせた、お子さんだけのカリキュラムで勉強が進められるから!
家庭教師のやる気アシストは、お子さんの志望校合格まで全力でサポートさせて頂きます!
お子さんにとって「成果が出る勉強法」ってどんな勉強法だと思いますか?
お子さんそれぞれに、個性や性格、学力の差もあります。そんな十人十色のお子さん全員に合う勉強法ってなかなかないんです。
たからこそ、受験生の今だけでもお子さんだけの勉強法で受験を乗り越えてみませんか?
やる気アシストには、決まったカリキュラムはありません。お子さんの希望や学力、得意や不得意に合わせて、お子さんだけのカリキュラムで指導を行っていきます。また、勉強法もお子さんそれぞれに合う合わないがあります。無料体験授業では、お子さんの性格や生活スタイルを見せていただき、お子さんにとって効率的な成果の出る勉強のやり方をご提案させて頂きます。

