







熊本県の2023年3月実施の令和5年度(2023年度)入学者の公立高校入試問題の解説をしています。
受験勉強において、過去問を解くことはとても効果的な勉強法です。ぜひ、受験までに一度挑戦し、問題の傾向を掴んでおきましょう。合わせて、対策などをたてられるととても良いですね。
また、過去問で苦手な点が見つかった場合は、そこを中心に試験日当日までにしっかりと対策しておきましょう。
次の計算をしなさい。
(1)$\frac{1}{7} + \frac{1}{2}$
(2)$6 + 4 \times (-3)$
(3)$8x + 9y + 7(x – y)$
(4)$8a^3b \div (-6ab^2) \times 9b$
(5)$(x + 1)(x – 5) + (x + 2)^2$
(6)$\sqrt{30} \div \sqrt{5} + \sqrt{54}$
(1)$\frac{9}{14}$
$\frac{1}{7} + \frac{1}{2} = \frac{2}{14} + \frac{7}{14} = \frac{9}{14}$
(2)-6
$6 + 4 \times (-3) = 6 + (-12) = -6$
(3)$15x + 2y$
$8x + 9y + 7(x – y) = 8x + 9y + 7x – 7y = 15x + 2y$
(4)$2a$
$8a^3b \div (-6ab^2) \times 9b = \frac{8a^3b \times 9b}{36a^2b^2} = 2a$
(5)$2x^2 – 1$
$(x + 1)(x – 5) + (x + 2)^2 = x^2 – 4x – 5 + x^2 + 4x + 4 = 2x^2 – 1$
(6)$4\sqrt{6}$
$\sqrt{30} \div \sqrt{5} + \sqrt{54} = \sqrt{\frac{30}{5}} + \sqrt{54} = \sqrt{6} + 3\sqrt{6} = 4\sqrt{6}$
次の各問いに答えなさい。
(1)一次方程式 $5x + 8 = 3x – 4$ を解きなさい。
(2)二次方程式 $2x^2 + 5x – 1 = 0$ を解きなさい。
(3)$y$ は $x$ に反比例し、$x = 2$ のとき $y = 3$ である。$x = 5$ のときの $y$ の値を求めなさい。
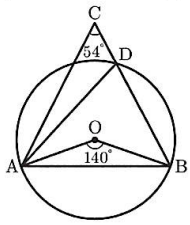
(4)右の図は、点Oを中心とする円で、2点A、Bは円Oの周上にある。点Cは円Oの外部にあり、$AC = BC$である。線分BCと円Oとの交点のうち、Bと異なる点をDとする。
$∠ACB = 54°$、$∠AOB = 140°$であるとき、$∠OAD$の大きさを求めなさい。
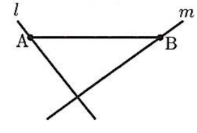
(5)右の図のように、平行でない2本の直線$l$、$m$があり、$l$上に点A、$m$上に点Bがある。線分AB上に、$l$と$m$の両方に接する円の中心Oをとりたい。
定規とコンパスを使って作図しなさい。なお、作図に用いた線は消さずに残しておくこと。
(6)次の図のように、箱Aと箱Bの2つの箱がある。箱Aには1、2、3、4の数字が1つずつ書かれた4枚のカードが、箱Bには1、2、3、4、5の数字が1つずつ書かれた5枚のカードが入っている。箱A、箱Bの順に、それぞれの箱から1枚ずつカードを取り出し、取り出した順に左から右にカードを並べて2けたの整数をつくる。
箱A
[1][2][3][4]
箱B
[1][2][3][4][5]
① つくることができる2けたの整数のうち、6の倍数は何個できるか、求めなさい。
② つくることができる2けたの整数が3の倍数になる確率を求めなさい。ただし、どのカードが取り出されることも同様に確からしいものとする。
(7)健太さんと直樹さんは、航平さんと、運動公園にある1周2400mのジョギングコースを走った。
3人ともスタート地点から同じ方向に一定の速さで走り、健太さんと直樹さんは、健太さんから直樹さんの順にそれぞれ1周ずつ、航平さんは一人で2周走った。
また、健太さんと直樹さんは次のように走った。
一方、航平さんは次のように走った。
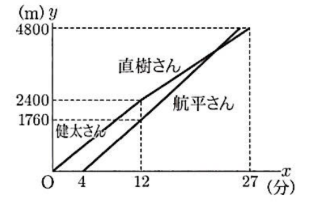
右の図は、健太さんが走り始めてから$x$分後の、健太さんと直樹さんが走った距離の合計を$y$mとして、$x$と$y$の関係をグラフに表したものに、航平さんが走ったようすをかき入れたものである。
① 航平さんの走る速さは毎分何mか、求めなさい。
② 航平さんが直樹さんと並んだのは、健太さんが走り始めてから何分何秒後か、求めなさい。
(1)-6
両辺移項して $2x = -12 \therefore x = -6$
(2) $\frac{-5 \pm \sqrt{33}}{4}$
解の公式より、$x = \frac{-5 \pm \sqrt{5^2 – 4 \times 2 \times (-1)}}{2 \times 2} = \frac{-5 \pm \sqrt{33}}{4}$
(3)$\frac{6}{5}$
$x$は$y$に反比例することより、$xy$が一定である。
$xy = 2 \times 3 = 6$
$x=5$のとき $5y = 6 \therefore y = \frac{6}{5}$
(4)$27^\circ$
円周角の定理より、$\angle ADB = \frac{1}{2}\angle AOB = 70^\circ$
$\angle CAD = \angle ADB – \angle ACD = 70^\circ – 54^\circ = 16^\circ$
ここで、$AC=BC、AO=BO$より、
$\angle CAB = \angle CBA = (180^\circ – 54^\circ) \div 2 = 63^\circ$、$\angle OAB = \angle OBA = (180^\circ – 140^\circ) \div 2 = 20^\circ$
$\therefore \angle OAD = \angle CAB – \angle CAD – \angle OAB = 63^\circ – 16^\circ – 20^\circ = 27^\circ$
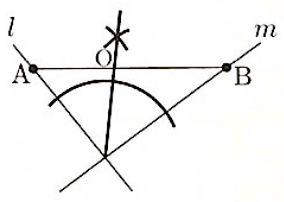
(5)図の通り
点Oから直線$l$、直線$m$に引いた垂線の長さが等しいことから、直線$l$と直線$m$の交点を点Cとして、$\angle ACB$の二等分線と線分ABの交点がOである
(6)
① 3個
$(A,B) = (1,2), (2,4), (4,2)$の3個
② $\frac{7}{20}$
すべての場合の数は、$4 \times 5 = 20$ (通り)
$3$の倍数の場合の数は、$(A,B) = (1,2), (1,5), (2,1), (2,4), (3,3), (4,2), (4,5)$の$7$通り
よって求める確率は$\frac{7}{20}$
(7)
① 220m
$1760 \div (12 – 4) = 220$ ∴毎分220m
② 22分40秒後
直樹さんの走る速さは$2400 \div 15 = 160$より毎分$160$m
航平さんは直樹さんに毎分$220 – 160 = 60$(m)ずつ近づくので、直樹さんが走り始めて$a$分後に航平さんが並んだとすると、
$a = 640 \div 60 = \frac{32}{3}$ (分)
よって、健太さんが走り始めてからの時間は$12 + \frac{32}{3} = 22 + \frac{2}{3}$ (分) ∴22分40秒後
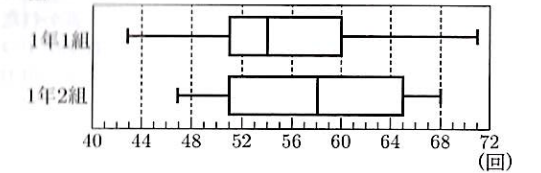
次の図は、美咲さんが通う高校の、1年1組39人と1年2組39人の反復横とびの回数の測定結果を、体育委員である美咲さんが箱ひげ図に表したものである。
このとき、次の各問いに答えなさい。
(1)次の【ア】、【イ】に当てはまる数を入れて、文を完成しなさい。
図の1組の箱ひげ図から、回数の範囲は【ア】回、四分位範囲は【イ】回であることがわかる。
さらに美咲さんは、その測定結果をヒストグラムに表した。
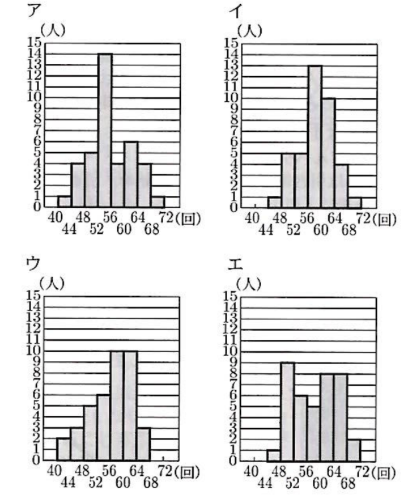
(2)次のア〜エのヒストグラムのうち、1組と2組を表しているものはどれか。それぞれ記号で答えなさい。
なお、ヒストグラムの階級は、40回以上44回未満、44回以上48回未満などのように、階級の幅を4回として分けている。
(3)美咲さんと同じ体育委員の大輔さん、雄太さん、恵子さんは、箱ひげ図やヒストグラムから読みとれることについて、それぞれ次のように考えた。
大輔さん:回数の範囲は、1組よりも2組の方が大きい。
由衣さん:回数の四分位範囲は、1組よりも2組の方が大きい。
雄太さん:回数が64回以上である人数は、1組よりも2組の方が多い。
恵子さん:1組の回数の平均は、60回である。
4人のうち、正しい読みとりをしているのは誰か。次のアからすべて選び、記号で答えなさい。
ア 大輔さん
イ 由衣さん
ウ 雄太さん
エ 恵子さん
(1)ア:28 イ:9
ア…71 – 43 = 28 (回)
イ…60 – 51 = 9 (回)
(2)1組:ア 2組:エ
1組…最小値が40回以上44回未満、最大値が68回以上72回未満であり、これにあてはまるヒストグラムはア。
2組…最小値が44回以上48回未満、最大値が68回以上72回未満であり、これにあてはまるヒストグラムはイとエ。2組の第1四分位数は51回であり、これは10番目の記録であることから、これにあてはまるエが正解である。
(3)イ・ウ
大輔さん:1組の範囲は71 – 43 = 28 (回)、2組の範囲は68 – 47 = 21 (回)、よって、正しくない。
由衣さん:1組の四分位範囲は60 – 51 = 9 (回)、2組の四分位範囲は65 – 51 = 14 (回) よって、正しい。
雄太さん:ヒストグラムより、回数が$64$回以上である人数は、1組が4 + 1 = 5 (回)、2組が8 + 2 = 10 (回) よって、正しい。
恵子さん:箱ひげ図やヒストグラムの情報だけでは各個人の詳細なデータはわからず、正確な平均値を求めることはできない。 よって、正しくない。
以上より、正しい読み取りをしているのは、イとウ。
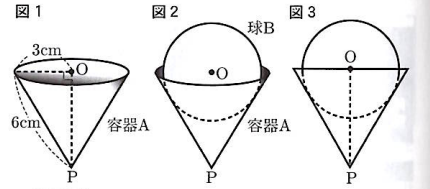
図1は、底面の半径が3cm、母線の長さが6cmの円すいの形をした容器Aである。底面の円の中心をO、頂点をPとすると、底面と線分OPは垂直に交わっている。図1の容器Aに球Bを、容器Aの内側の面にぴったりつくように入れたところ、図2のように球Bの中心がOと重なった。図3は、図2の立面図である。
このとき、次の各問いに答えなさい。ただし、円周率は$\pi$とし、容器Aの厚さは考えないものとする。また、根号がつくときは、根号のついたままで答えること。
(1)容器Aの容積を求めなさい。
(2)容器Aの側面積を求めなさい。
(3)球Bの半径を求めなさい。
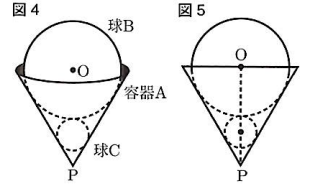
(4)図4のように、容器Aと球Bの間にちょうど入るような球Cを入れた。図5は、図4の立面図である。球Cの体積を求めなさい。
(1)$9\sqrt{3}\pi (cm^2)$
底面の円の任意の点を点$Q$とすると、$\angle POQ=90^\circ$、$PQ=6$cm、$OQ=3$cm
三平方の定理より、$OP=\sqrt{6^2 – 3^2} = 3\sqrt{3}$ (cm)
したがって、容器Aの容積は
$\frac{1}{3} \times \pi \times 3^2 \times 3\sqrt{3} = 9\sqrt{3}\pi (cm^2)$
(2)$18\pi (cm^2)$
容器Aを展開すると、半径$6$の扇形となる。
中心角は、$360^\circ \times \frac{3 \times 2\pi}{6 \times 2\pi} = 180^\circ$であるから、
容器Aの側面積は、$\pi \times 6^2 \times \frac{180}{360} = 18\pi (cm^2)$
(3)$\frac{3\sqrt{3}}{2} (cm)$
球 $B$ と線分 $PQ$ の接点を点 $R$ とする。
$\triangle POR \backsim \triangle POQ$ より、$PO:PQ=OR:QO$
$3\sqrt{3}:6 = OR:3 \qquad OR=\frac{3\sqrt{3}}{2}$
よって球 $B$ の半径は、$\frac{3\sqrt{3}}{2}$ (cm)
(4)$\frac{\sqrt{3}}{2}\pi (cm^3)$
球 $C$ と線分 $PQ$ の接点を点 $S$ とし、$ST=r$とおく。
$\triangle PTS \backsim \triangle POR$ より、$PT:PO=ST:RO$
$\left(\frac{3\sqrt{3}}{2} – r\right) : 3\sqrt{3} = r : \frac{3\sqrt{3}}{2} \qquad r = \frac{\sqrt{3}}{2}$
したがって、球 $C$ の体積は、$\frac{4}{3}\pi \times \left(\frac{\sqrt{3}}{2}\right)^3 = \frac{\sqrt{3}}{2}\pi(cm^3)$
右の図のように、関数$y = ax^2$ ($a$は定数) $\cdots$① のグラフ上に$2$点A、Bがある。Aの座標は$(-1, 2)$、Bの$y$座標は8で、Bの$x$座標は正である。また、点Cは直線ABと$y$軸との交点であり、点Oは原点である。
このとき、次の各問いに答えなさい。
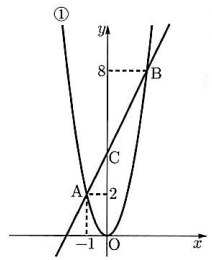
(1)$a$の値を求めなさい。
(2)点Bの$x$座標を求めなさい。
(3)直線ABの式を求めなさい。
(4)線分BC上に2点B、Cとは異なる点Pをとる。$\triangle OPC$の面積が、$\triangle AOB$の面積の$\frac{1}{4}$となるときのPの座標を求めなさい。
(1)$a = 2$
$y = ax^2$に、$x = -1, y = 2$を代入すると、$2 = a \times (-1)^2$、$a = 2$
(2)$x = 2$
$y = 2x^2$に、$y = 8$を代入すると、$8 = 2x^2$となり、$x = \pm2$
$x > 0$より、$x = 2$
(3)$y = 2x + 4$
求める式を$y = bx + c$とおく。
点Aを通るので、$x = -1, y = 2$を代入すると、$2 = -b + c$ …①
点Bを通るので、$x = 2, y = 8$を代入すると、$8 = 2b + c$ …②
①②を連立して解くと、$b = 2, c = 4$
よって直線 $AB$ の式は $y = 2x + 4$
(4)$P\left(\frac{3}{4}, \frac{11}{2}\right)$
点$P(t, 2t + 4)$とすると、$C(0,4)$より、$\triangle OCP = \frac{1}{2} \times 4 \times t = 2t$
また、$\triangle OAB = \frac{1}{2} \times 4 \times {2 – (-1)} = 6$
$\triangle OCP = \frac{1}{4} \triangle OAB$ だから、
$2t = \frac{1}{4} \times 6 \qquad \therefore t = \frac{3}{4}$
よって、$P\left(\frac{3}{4}, \frac{11}{2}\right)$
右の図は、点Oを中心とする円で、線分ABは円の直径である。点Cは$\stackrel{\frown}{AB}$上にあり、点Dは線分BC上にあって、$OD // AC$である。また、点EはODの延長とBにおける円の接線との交点である。
このとき、次の各問いに答えなさい。
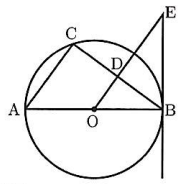
(1)$\triangle ABC \infty \triangle OEB$であることを証明しなさい。
(2)$AB = 10$cm、$BC = 8$cm のとき、
① 線分ACの長さを求めなさい。
② 線分BEの長さを求めなさい。
(1)
$\triangle ABC$ と $\triangle OEB$ において、
線分 $AB$ は円 $O$ の直径であるから、$\angle ACB=90^\circ$
直線 $BE$ は円 $O$ の接線であるから、$\angle OBE=90^\circ$
よって、$\angle ACB=\angle OBE$ …①
$AC \parallel OE$ より、同位角は等しいから、
$\angle BAC=\angle EOB$ …②
①②より、2組の角がそれぞれ等しいから、$\triangle ACB \backsim \triangle OEB$
(2)① $AC=\sqrt{10^2 – 8^2} = 6$(cm) ② $EB=\frac{20}{3}$(cm)
① $\angle ACB= 90^\circ$より、三平方の定理から、
$AC=\sqrt{10^2 – 8^2} = 6$(cm)
② $\triangle ACB \backsim \triangle OEB$ より、
$BC:EB=AC:OB$
$8:EB=6:5 \qquad \therefore EB=\frac{20}{3}$(cm)
選択問題Aと同じ問題の為省略
(1)~(4)は選択問題Aと同じ問題の為省略
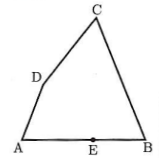
(5)右の図のように、四角形ABCDがあり、辺AB上に点Eがある。点Eで辺ABに接し、辺CDにも接する円の中心Oを、定規とコンパスを使って作図しなさい。
なお、作図に用いた線は消さずに残しておくこと。
(6)下の図のように、箱A、箱Bの2つの箱がある。箱Aには2、4の数字が1つずつ書かれた2枚の赤いカードと2の数字が書かれた1枚の白いカードが、箱Bには3、6の数字が1つずつ書かれた2枚の赤いカードと3、4、6の数字が書かれた1枚の白いカードが入っている。
箱Aと箱Bからそれぞれ1枚ずつカードを取り出し、取り出した2枚のカードを用いて次のように得点を決めることにした。
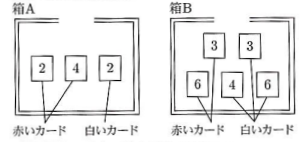
① 得点の最大値を求めなさい。
② 次の【ア】、【イ】に当てはまる数を入れて、文を完成しなさい。ただし、どのカードが取り出されることも同様に確からしいものとする。
得点が【ア】点となる確率が最も高く、その確率は【イ】である。
(7)健太さんと直樹さんは、航平さんと、運動公園にある1周2400mのジョギングコースを走った。
健太さんと直樹さんはスタート地点から1周ずつ、健太さんから直樹さんの順にそれぞれ一定の速さで走った。健太さんは走り始めてから12分後に1周を走り終え、直樹さんへ引き継いだ。直樹さんは引き継ぎと同時に健太さんと同じ方向に走り始め、引き継ぎから15分後に1周を走り終えた。
一方、航平さんは一人で2周を走ることとし、健太さんが走り始めて$a$分後に、毎分240mの速さで健太さんと同じスタート地点から健太さんと同じ方向に走り始めた。健太さんが走り終えたとき、航平さんは1周目の途中を走っており、健太さんと240m離れていた。航平さんは2周目の途中で直樹さんを追いこし、その後も毎分240mの速さで2分以上走ったが、ある地点で$b$分間立ち止まった。航平さんは、直樹さんが航平さんに並ぶと同時に直樹さんと同じ速さで一緒に走り、2周を走り終えた。
右の図は、健太さんが走り始めてから$x$分後の、健太さんと直樹さんが走った距離の合計を$y$mとして、$x$と$y$の関係をグラフに表したものである。
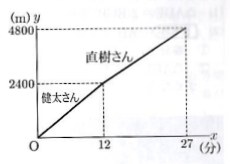
① $a$の値を求めなさい。
② 航平さんが直樹さんと最初に並んだのは、健太さんが走り始めてから何分後か、求めなさい。
③ $b$の値の範囲を求めなさい。
(5)
直線 $AB$ は円 $O$ の接線となるので、点 $E$ を通り直線 $AB$ に対する垂線を作図する。…①
次に、点 $O$ から直線 $AB$、直線 $CD$ までの距離は等しいので、直線 $AB$,直線 $CD$ の交点を点 $F$ として、$\angle CFB$ の二等分線を作図すれば、①との交点が点 $O$ である。
(6)① $4 \times 6 = 24$ ② $\frac{4}{3 \times 5} = \frac{4}{15}$
① 箱 $A$ から赤いカードの$4$、箱 $B$ から赤いカードの$6$を取り出したとき最大値となり、$4 \times 6 = 24$(点)
② 樹形図を描くと、得点が$8$ア点となるのが$4$通りで最も多く、確率は、$\frac{4}{3 \times 5} = \frac{4}{15}$
(7)① 3 ② 15 ③ $1 \leqq b < 4$
①健太さんが走り終えたとき、航平さんはスタート地点から$2400 – 240 = 2160$(m)進んだところにいる。
航平さんは毎分 $240$m の速さで走るので、$12 – 2160 \div 240 = 12 – 9 = 3$(分後)
②$(4800 – 2400) \div (27 – 12) = 160$ より、直樹さんは毎分 $160$m で走る。
直樹さんが走り始めたときの航平さんとの差は $240$m であるから、直樹さんが走り始めてから航平さんが最初に並ぶまでの時間は$240 \div (240 – 160) = 3$(分)
よって、健太さんが走り始めてから $12 + 3 = 15$(分後)
③航平さんが直樹さんに追いついてからさらに $2$ 分間走ったとき、航平さんは直樹さんから$(240 – 160) \times 2 = 160$(m)離れており、これを立ち止まって待つには$160 \div 160 = 1$(分)かかる。よって$b \geqq 1$ …①
航平さんが立ち止まらずに $2$ 周走ったとき、航平さんは直樹さんから${(240 – 160) \times (2400 + 240) – 240 \times 3} = 640$(m)離れており、これを立ち止まって待つには$640 \div 160 = 4$(分)かかる。
$b = 4$ のとき、航平さんが立ち止まったあとに直樹さんと一緒に走ることができないのでで、$b < 4$ …②
①,②より $1 \leqq b < 4$
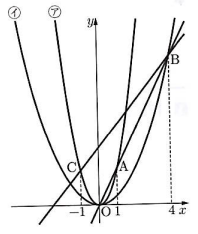
右の図のように、2つの関数$y = 2x^2 \cdots$㋐、$y = ax^2$ ($a$は定数)$\cdots$㋑のグラフがある。
点Aは関数㋐のグラフ上にあり、$x$座標は1である。点Bは関数㋑のグラフ上にあり、$x$座標が4で、直線ABは原点Oを通る。また、点Cは関数㋐のグラフ上にあり、$x$座標は-1である。
このとき、次の各問いに答えなさい。
(1)$a$の値を求めなさい。
(2)直線BCの式を求めなさい。
(3)点Bから$x$軸にひいた垂線と$x$軸との交点をD、直線BCと$y$軸との交点をEとする。関数㋑のグラフ上において2点O、Bの間に点Pをとり、点Pから$x$軸にひいた垂線と$x$軸との交点をQとする。また、直線PQと関数㋐のグラフとの交点をRとする。$PR = QD$のとき、
① 点Pの$x$座標を求めなさい。
② 線分CE上に点Sをとる。$\triangle SPR$の面積が、$\triangle SQD$の面積の$\frac{5}{6}$倍となるときのSの座標を求めなさい。
(1)$a = \frac{1}{2}$
点 $A(1,2)$ より直線 $AB$ の式は$y = 2x$
点 $B$ の$x$座標が$4$だから、これに代入して$y = 8$、よって点 $B(4,8)$
$y = ax^2$に$x = 4, y = 8$を代入すると、$8 = 16a \qquad \therefore a = \frac{1}{2}$
(2)$y = \frac{6}{5}x + \frac{16}{5}$
求める式を$y = cx + d$とおくと、
$B(4,8)$ より、$8 = 4c + d$ …①
$C(-1,2)$ より、$2 = -c + d$ …②
①,②を連立して解くと、$c = \frac{6}{5}, d = \frac{16}{5}$
したがって、$y = \frac{6}{5}x + \frac{16}{5}$
(3)① $t = \frac{4}{3}$ ② $S\left(-\frac{2}{3}, \frac{12}{5}\right)$
① 点 $P$ の$x$座標を$t$とする。($0 < t < 4$)
$P\left(t, \frac{1}{2}t^2\right), R(t, 2t^2), PR=QD$ より、$2t^2 – \frac{1}{2}t^2 = 4 – t$
$3t^2 + 2t – 8 = 0$
解の公式より、$t = \frac{-2 \pm \sqrt{2^2 – 4 \times 3 \times (-8)}}{2 \times 3} = \frac{4}{3}, -2$
$0 < t < 4$ より、$t = \frac{4}{3}$
② 点Sの$x$座標を$s$とする。($-1 < s < 0$)
$S\left(s, \frac{6}{5}s + \frac{16}{5}\right), \triangle SPR = \frac{5}{6} \triangle SQD$ より、
$\frac{1}{2} \times PR \times \left(\frac{4}{3} – s\right) = \frac{5}{6} \times \frac{1}{2} \times QD \times \left(\frac{6}{5}s + \frac{16}{5}\right)$
$PR=QD$ より両辺を$\frac{1}{2}PR$で割って
$\frac{4}{3} – s = \frac{5}{6}\left(\frac{6}{5}s + \frac{16}{5}\right) \qquad \therefore s = -\frac{2}{3}$
したがって、$S\left(-\frac{2}{3}, \frac{12}{5}\right)$
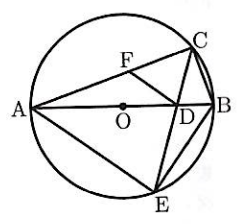
右の図は、点Oを中心とする円で、線分ABは円の直径である。
$\stackrel{\frown}{AB}$上に点Cを、$AC > BC$となるようにとる。点Dは線分OB上にあり、点EはCDの延長とCを含まない$\stackrel{\frown}{AB}$との交点である。また、点Fは線分AC上にあって、$FD // AE$である。
このとき、次の各問いに答えなさい。ただし、根号がつくときは、根号のついたままで答えること。
(1)$\triangle ADF \infty \triangle ECB$であることを証明しなさい。
(2)$AB = 6$cm、$BC = 2$cm、$AE = CE$のとき、
① 線分AEの長さを求めなさい。
② $\triangle ADF$の面積は、$\triangle ECB$の面積の何倍であるか、求めなさい。
(1)$\triangle ADF \backsim \triangle ECB$
$\triangle ADF$ と $\triangle ECB$ において、$AE \parallel FD$ より、錯覚は等しいから、$\angle EAB=\angle FDA$
$\angle EAB$ と $\angle BCE$ は$\stackrel{\frown}{BE}$に対する円周角であるから、$\angle EAB=\angle BCE$
よって、$\angle FDA=\angle BCE$ …①
$\angle FAD$ と $\angle BEC$ は$\stackrel{\frown}{BC}$に対する円周角であるから、$\angle FAD=\angle BEC$ …②
①,②より、2組の角がそれぞれ等しいから、$\triangle ADF \backsim \triangle ECB$
(2)① $2\sqrt{6}$(cm) ② $\triangle ADF=\frac{24}{25}\triangle ECB$
①$\angle ACB= 90^\circ$より、三平方の定理から、$AC=\sqrt{6^2 – 2^2} = 4\sqrt{2}$ (cm)
点 $E$ から線分 $AC$ に垂線 $EH$ を引く。
$AH=CH=\frac{1}{2}AC=2\sqrt{2}$ (cm)
$AE=CE$ であるから、点 $O$ は線分 $EH$ 上にある。
ここで、$\triangle AOH$ と $\triangle ABC$ において、$\angle AHO= 90^\circ=\angle ACB, \angle OAH=\angle BAC$ より、
2組の角がそれぞれ等しいから、$\triangle AOH \backsim \triangle ABC$
よって、$OH:BC=AO:AB \qquad OH=1$(cm)
$OE=\frac{1}{2}AB= 3$(cm) であるから、$EH= 1 + 3 = 4$(cm)
$\triangle EHA$ において、三平方の定理より、$AE=\sqrt{4^2 + (2\sqrt{2})^2} = 2\sqrt{6}$(cm)
②$OH \parallel BC$ より $EH \parallel BC$ であるから、$\triangle DBC \backsim \triangle DOE$ である。
$DB:DO=BC:OE=2:3$ より、$DO=\frac{3}{2+3}OB=\frac{3}{5} \times 3=\frac{9}{5}$ (cm)
よって、$AD3 + \frac{9}{5} = \frac{24}{5}$ (cm)
$\triangle ADF$ と $\triangle ECB$ の相似比は、$AD:EC=\frac{24}{5}:2\sqrt{6} = 12:5\sqrt{6}$
したがって、面積比は、$12^2:(5\sqrt{6})^2 = 24:25$
以上より、$\triangle ADF=\frac{24}{25}\triangle ECB$
家庭教師のやる気アシストは、熊本県にお住まいの受験生のお子さんを毎年たくさん指導をさせていただき、合格に導いています。
高い合格率の秘訣は、指導経験豊富な先生の指導力に加え、1対1の指導でお子さん一人ひとりの状況に合わせた、お子さんだけのカリキュラムで勉強が進められるから!
家庭教師のやる気アシストは、お子さんの志望校合格まで全力でサポートさせて頂きます!
お子さんにとって「成果が出る勉強法」ってどんな勉強法だと思いますか?
お子さんそれぞれに、個性や性格、学力の差もあります。そんな十人十色のお子さん全員に合う勉強法ってなかなかないんです。
たからこそ、受験生の今だけでもお子さんだけの勉強法で受験を乗り越えてみませんか?
やる気アシストには、決まったカリキュラムはありません。お子さんの希望や学力、得意や不得意に合わせて、お子さんだけのカリキュラムで指導を行っていきます。また、勉強法もお子さんそれぞれに合う合わないがあります。無料体験授業では、お子さんの性格や生活スタイルを見せていただき、お子さんにとって効率的な成果の出る勉強のやり方をご提案させて頂きます。

