この投稿では、二次方程式の利用について解説していきます。二次方程式についての問題を解説していきます。

授業の予習復習や定期テスト対策にご活用ください！

その他の数学の勉強記事もこちらから見ることができます。ぜひご覧ください！

1. 二次方程式の利用（数の性質）

方程式には、一次方程式、二次方程式、連立方程式などいろいろありますが、解くためのステップはいつも同じです。

この順番です。これを踏まえて例題に取り組んでいきましょう！

例題１：ある整数 x に 3 を加えた数の平方は、16 である。ｘの値を求めなさい。

---

《 解答・解説 》

この問題の場合は手順の①はすでにやってある状態なので、②からやっていきましょう。

ある整数 x に 3 を加えた数　はｘ+３ということ。平方とは2乗のことなので、ｘ+３の平方は16　というのは（ｘ+３）² ＝ 16　という意味になります。これで②が出来ました。

さいごにこの方程式を解けば答えになります。

2. 二次方程式の利用（面積）

例題２：正方形の縦を３cm短くし、横を４cm長くして長方形を作ったらその面積は 60cm²になった。元の正方形の１辺の長さを求めなさい。

---

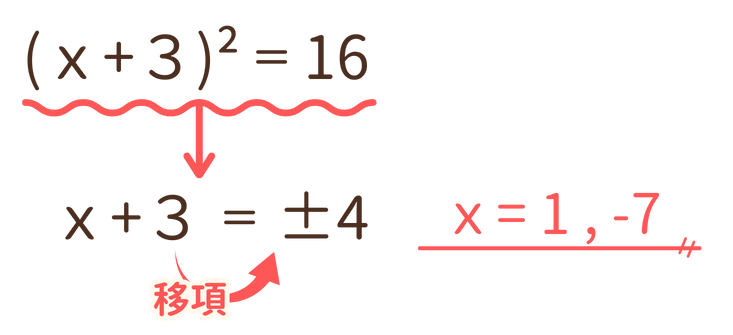
《 解答・解説 》

この問題でもやることは同じです。①から順番にやっていきましょう。まずは「ｘ」を置いて方程式を立てていきます。

元の正方形の１辺の長さを求めなさい。とあるので正方形の辺をｘとします。よって、長方形になった時の縦はｘー3、横はｘ＋4とします（下の図で確認しましょう！）

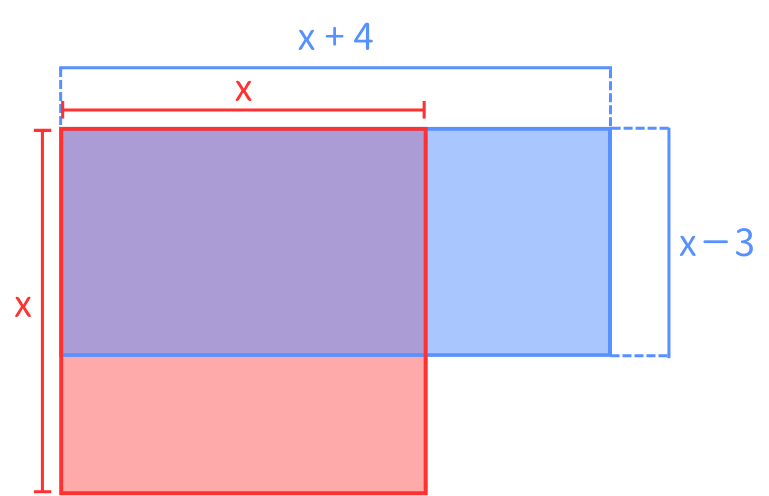
ｘを置くことができたので②に移ります。問題文に長方形の長さは60㎠であったとあるので、(ｘ－3)(ｘ＋4)＝60　という式が立てられます。

では最後に方程式を解いてｘの値を求めましょう。

ただ、最後に注意が必要です。今回は正方形の辺の長さを求めています。そのため、－(マイナス)の値はありません。そのため、今回は解が８と-9ですが、-9は解答としてふさわしくありません。よって答えは８cmです。

＼小・中・高校生の勉強にお悩みのある方へ／

3. 二次方程式の利用（動点）

△ABCはBC=12cm、AC=6cm、∠ACB＝90°の直角三角形である。点Pは頂点Ｃを出発して毎秒２cmでBまで進む。同時に点Qは頂点Aを出発して毎秒１cmでCまで進む。△PCQの面積が９cm²になるのは出発から何秒後か。

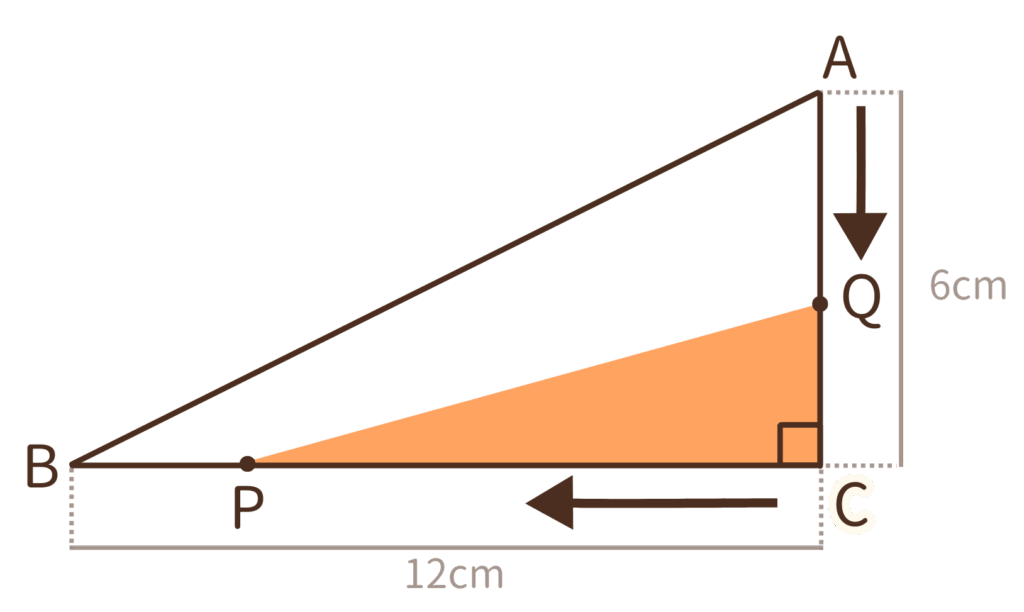
求められているのは△PCQの面積が９cm²になるのは出発から何秒後か、ということなので△PCQの面積が９cm²になる秒数をｘとします。するとｘ秒後のQCの長さは６－ｘ、PCは 2ｘ(０≦ｘ≦9) と表現することができます。

ここが分かれば△PCQの面積を求める式が立てられます。→ (底辺：2ｘ)・(高さ：６－ｘ) ・ 1/2 ＝ 9 cm²

この式を解いてｘの値を求めましょう。

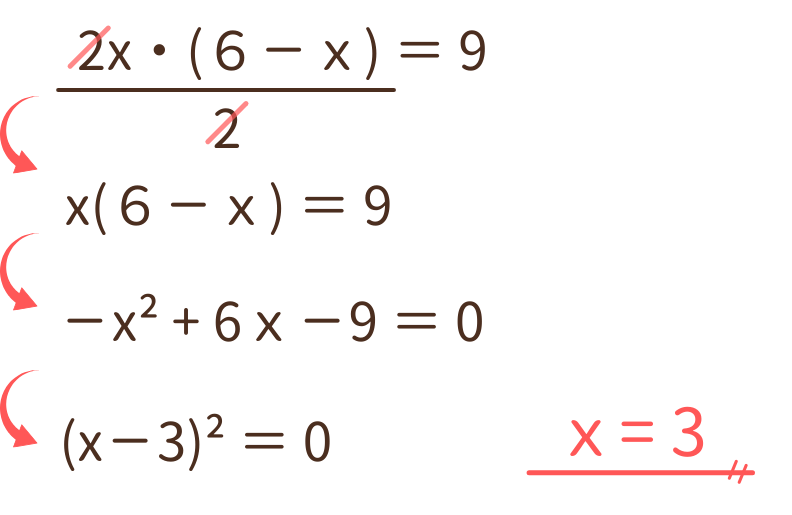
最後までお読みいただきありがとうございました。

他にも様々なお役立ち情報をご紹介しているので、ぜひご参考にしてください。
質問などございましたら、お気軽にお問い合わせください！