【数学】反比例の関係
前回は比例のグラフの書き方について学んでいきました。
今回は反比例の関係について詳しく解説していきたいと思います。
反比例の鍵はｘとｙの積が○○です！では見ていきましょう。
目次
1.反比例
早速ですが、縦の長さがｘｃｍ、横の長さがｙｃｍ、面積が24ｃｍ²の長方形を考えていきましょう。
| ｘ | 1 | 2 | 3 | 4 | 5 | 6 |
| ｙ | 24 | 12 | 8 | 6 | 4.8 | 4 |
このようにｘが2倍、3倍となると、ｙが1/2倍、1/3倍となる関係を反比例の関係にあると言います。
2.反比例の式
比例の式はｙ=axで表すことが出来ました。
反比例も同じ様に表すこと出来て、「y=a/ｘ」の形で表すことができます。aを比例定数と呼びます。
前章で触れた内容はｙ＝24/ｘと表すことができます。
例題
次の関係をｙをｘの式で表す問題です。
①50ｋｍの道を時速ｘｋｍの車で移動するとｙ時間かかる。
②100ｃｍのテープをｘ等分すると、1本の長さはｙｃｍになる。
③面積が12ｃｍ²の三角形の底辺をｘｃｍ、高さをｙｃｍとする。
④20人の子供にｘ本ずつ鉛筆を配るときに必要な鉛筆の本数はｙ本になる。
解説
①時間を求めるときは「距離÷速さ」で求めることができます。
よって、ｙ＝50÷ｘ＝50/ｘが答えとなります。
②具体的な数を代入して考えていきましょう。
ｘ＝1の時、ｙ＝100ｃｍ
ｘ＝2の時、ｙ＝50ｃｍ
ｘ＝4の時、ｙ＝25ｃｍ
となります。
よって答えはｙ＝100/ｘとなります。
③三角形の面積は「底辺×高さ÷2」で求めることができます。
よって、ｘ×ｙ÷2＝12となるので、
ｙ＝24/ｘとなります。
④こちらも具体的な数を代入して考えていきましょう。
ｘ＝1の時、ｙ＝20
ｘ＝2の時、ｙ＝40
ｘ＝3の時、ｙ＝60
となります。
よって答えはｙ＝20ｘとなります。最後の問題は引っかけで比例の式となります。
＼小・中・高校生の勉強にお悩みのあるお子さん・保護者様へ／
＼小・中・高校生の勉強にお悩みのある方へ／
3.反比例の式を求める
この章ではｘとｙの値が分かったときに式を求める簡単な方法を紹介したいと思います。
冒頭でも触れましたが、反比例の式はｘとｙの積が必ず「一定」になります。
前章の例題の②の式で見てみると、
ｘ＝1の時、ｙ＝100なのでｘ×ｙ＝100
ｘ＝2の時、ｙ＝50なのでｘ×ｙ＝100
ｘ＝4の時、ｙ＝25なのでｘ×ｙ＝100
すなわち、ｘとｙを掛けたときの値が比例定数となることが最大のポイントです！
例題
ｙがｘに反比例し、ｘ、ｙの値が次の値になるときにｙをｘの式で表す問題です。
①ｘ＝3，ｙ＝－2
②ｘ＝2，ｙ＝4
③ｘ＝－4，ｙ＝－1/2
解説
反比例の式はｘとｙの積が必ず比例定数となります。
①a=3×（－2）＝－6
よって、ｙ＝－6/ｘが答えとなります。
②a＝2×4＝8
よって、ｙ＝8/ｘが答えとなります。
③a＝－４×（－1/2）＝2
よって、ｙ＝2/ｘが答えとなります。
＼小・中・高校生の勉強にお悩みのあるお子さん・保護者様へ／
＼小・中・高校生の勉強にお悩みのある方へ／
4.反比例のグラフ
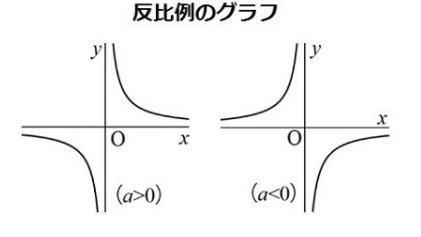
反比例のグラフは上図のように原点を中心とした対称な2つの曲線になります。
このような曲線のことを双曲線と呼びます。
グラフからの式の読み取り方も、ｘとｙの積が必ず比例定数となることに注目すれば簡単です。実際に問題を解いてみましょう。
例題
下図の①～④のグラフを表す式を書く問題です。
解説
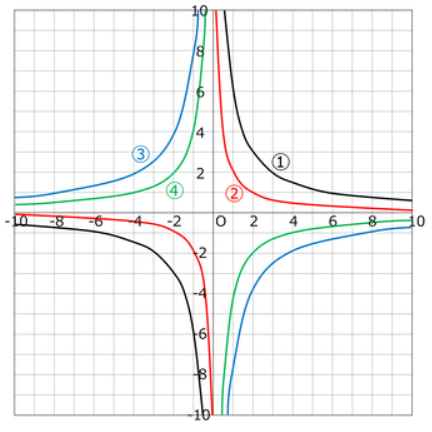
①このグラフは点（3，2）を通るのでa＝3×2＝6
よって、ｙ＝6/ｘが答えです。
②このグラフは点（2，1）を通るのでa＝2×1＝2
よって、ｙ＝2/ｘが答えです。
③このグラフは点（－4，2）を通るのでa＝－4×2＝－8
よって、ｙ＝－8/ｘが答えです。
④このグラフは点（－2，2）を通るのでa＝－2×2＝－4
よって、ｙ＝－4/ｘが答えです。
この記事を書いた人
趣味：お城巡り
関西大学大学院を卒業後、小６・中３・高３の受験生を主に指導をしてきました。学生の悩み相談を受けているうちに勉強に悩む子を救ってあげたいという気持ちが強まり学習アドバイザーとなりました。勉強に悩む保護者さまやお子さんにお役に立てる記事を配信していければと思います。
Instagram・ⅹなどでも情報発信中ですので、ぜひフォローください！
