【群馬県】令和5年度/2023年度入学者高校入試選抜試験：数学の解説
群馬県の2023年3月実施の令和5年度（2023年度）入学者の公立高校入試問題の解説をしています。
受験勉強において、過去問を解くことはとても効果的な勉強法です。ぜひ、受験までに一度挑戦し、問題の傾向を掴んでおきましょう。合わせて、対策などをたてられるととても良いですね。
また、過去問で苦手な点が見つかった場合は、そこを中心に試験日当日までにしっかりと対策しておきましょう。
大問1 小問集合
問題文
次の（1）～（9）の問いに答えなさい。
（1）次の①～③の計算をしなさい。
①$2-(-4)$
②$6a^2 \times \frac{1}{3}a$
③$-2(3x-y)+2x$
（2）次の①、②の方程式を解きなさい。
①$6x-1=4x-9$
②$x^2+5x+3=0$
（3）次のア～エのうち、絶対値が最も小さい数を選び、記号で答えなさい。
ア $3$ イ $-5$ ウ $-\frac{5}{2}$ エ $2.1$
（4）関数$y=ax^2$のグラフが点（-2，-12）を通るとき、aの値を求めなさい。
（5）次の図において、l//mのとき、∠xの大きさを求めなさい。
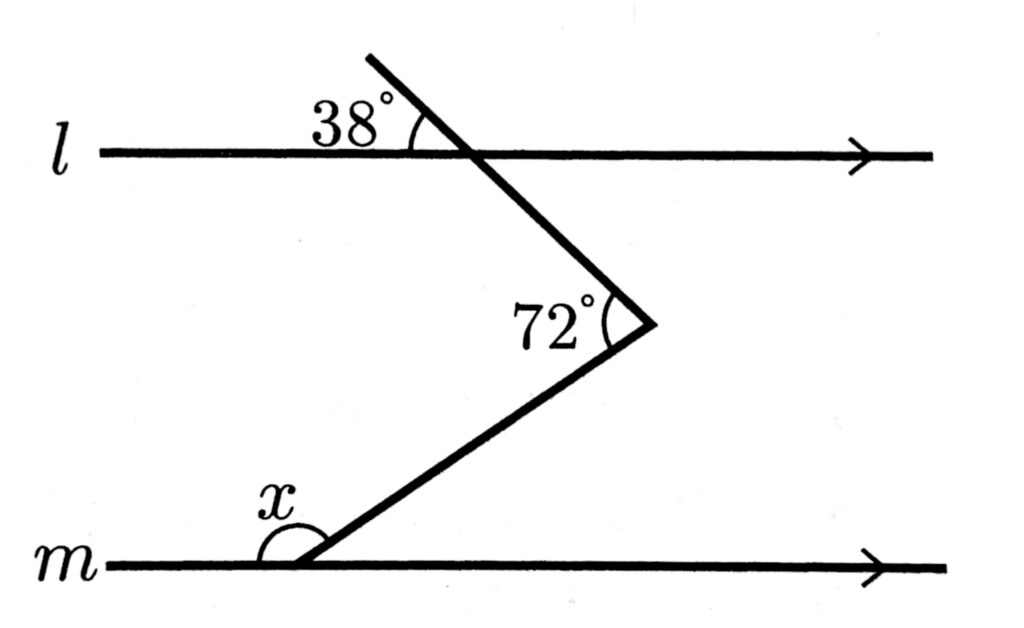
（6）$a=2+\sqrt{5}$のとき、$a^2-4a+4$の値を求めなさい。ただし、答えを求める過程を書くこと。
（7）1，2，3，4の数が1枚ずつ書かれた4枚のカードを袋の中に入れる。この袋の中をよく混ぜてからカードを1枚引いて、これを戻さずにもう1枚引き、引いた順に左からカードを並べて2けたの整数をつくる。このとき、2けたの整数が32以上になる確率を求めなさい。
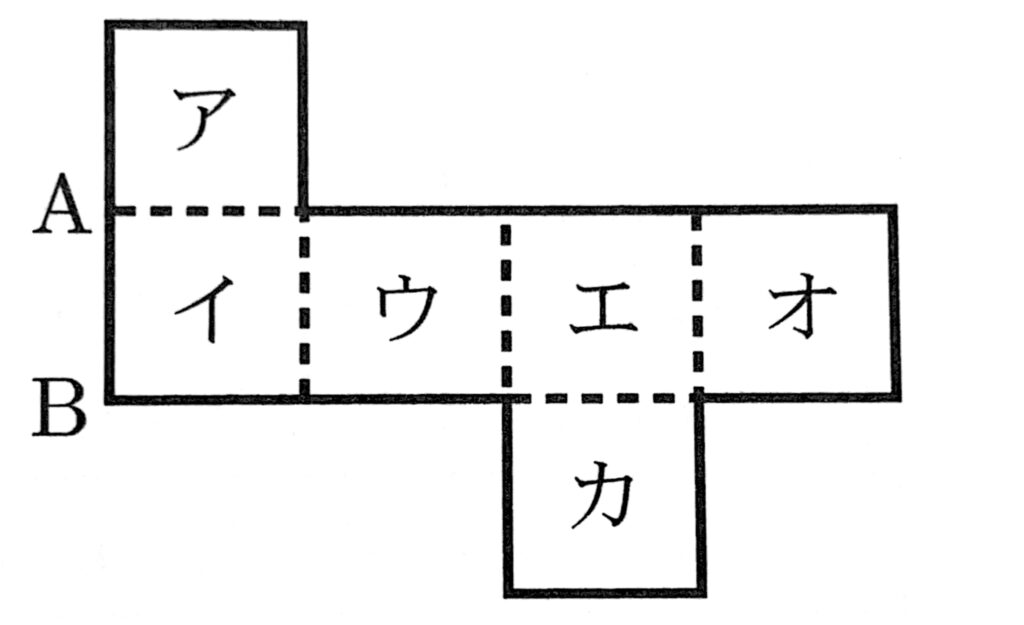
（8）次の図は、立方体の展開図である。この展開図を組み立てて立方体をつくるとき、面イの一辺である辺ABと垂直になる面を、面ア～カからすべて選び、記号で答えなさい。
（9）次の図は、ある部活動の生徒15人が行った「20ｍシャトルラン」の回数のデータを、箱ひげ図にまとめたものである。後のア～オのうち、図から読み取れることとして必ず正しいといえるものをすべて選び、記号で答えなさい。
ア 35回だった生徒は1人である。
イ 15人の最高記録は95回である。
ウ 15人の回数の平均は57回である。
エ 60回以下だった生徒は少なくとも9人いる。
オ 60回以上だった生徒は4人以上いる。
解答・解説
（1）① 6 ② $2a^3$ ③ $-4x+2y$
① $2+4=6$
② $\frac{6a^2 \times a}{3} = 2a^3$
③ $-6x + 2y + 2x = -4x + 2y$
（2）① $x=-4$ ② $x=\frac{-5\pm\sqrt{13}}{2}$
① $6x – 4x = -9 + 1, 2x = -8, x = -4$
② 解の公式を用いて、$x = \frac{-5\pm\sqrt{5^2-4\times1\times3}}{2\times1} = \frac{-5\pm\sqrt{13}}{2}$ となる。
（3）エ
絶対値は数直線上で原点からの距離だから、$3$の絶対値は$3$、$-5$の絶対値は$5$、$-\frac{5}{2}$の絶対値は$\frac{5}{2}$、$2.1$の絶対値は$2.1$である。$\frac{5}{2}=5 \div 2 = 2.5$より、$2.1 < 2.5 < 3 < 5$, $2.1 < \frac{5}{2} < 3 < 5$だから、絶対値が最も小さい数は、絶対値が$2.1$である$2.1$となる。
（4）-3
関数$y = ax^2$のグラフが点(-2,-12)を通るので、$y = ax^2$に $x=-2, y=-12$を代入して、$-12 = a \times (-2)^2$より、$a = -3$である。
（5）146°
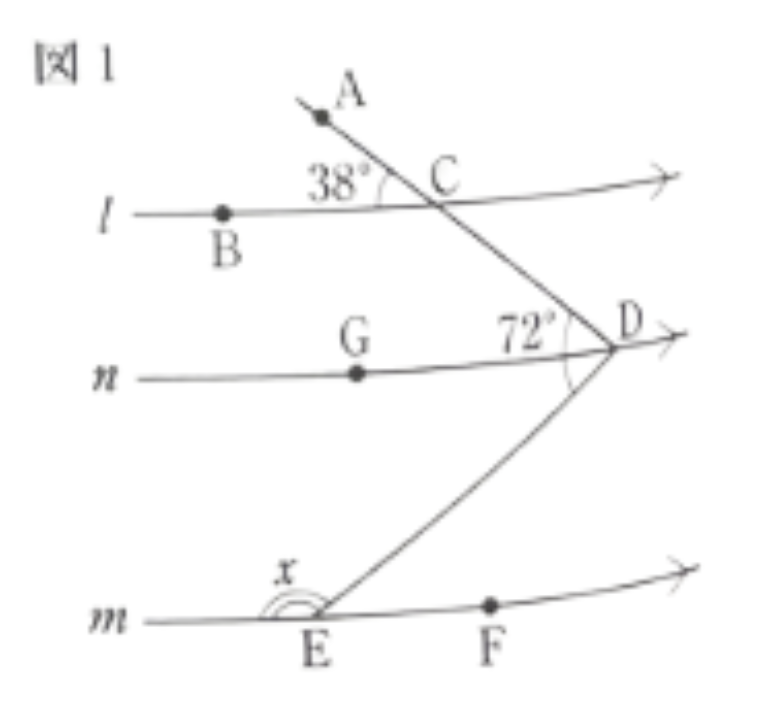
図1のように、6点 A~F を定め、点Dを通り直線nを引き、直線n上の点Dより左に点Gをとる。$l // n$ より、同位角は等しいから、$\angle\text{CDG}=\angle\text{ACB}=38^\circ$である。
これより、$\angle\text{GDE}=\angle\text{CDE}-\angle\text{CDG}=72^\circ – 38^\circ = 34^\circ$となる。
$n // m$ より、錯角は等しいから、$\angle\text{DEF}=\angle\text{GDE}=34^\circ$である。
よって$\angle x=180^\circ – \angle\text{DEF}=180^\circ – 34^\circ = 146^\circ$である。
（6） 5
与式=$(a-2)^2$として、これに$a = 2+\sqrt{5}$を代入すると、$(2+\sqrt{5}-2)^2 = (\sqrt{5})^2 = 5$となる。
（7）$\frac{5}{12}$
4枚のカードの中からカードを1枚ずつ2回引くとき、1回目の引き方は4通りあり、引いたカードをもとに戻さないので、残りが3枚より、2回目の引き方は3通りある。
よって、カードの引き方は、全部で$4 \times 3=12$ (通り)あり、2けたの整数も12通りつくれる。このうち、つくった数が3以上になるのは、(1回目、2回目)=(3,2), (3,4), (4,1), (4,2), (4,3)の5通りあるから、求める確率は$\frac{5}{12}$となる。
（8）ア、カ
辺 AB と垂直になる面は、面アと面力である。
（9）イ、オ
ア・・誤。最小値が35回だから、35回の生徒は少なくとも 1 人はいるが、何人いるかは読み取れない。
イ・・正。最も値が95回である。
ウ・・誤。57回となっているのは中央値(第 2 四分位数)である。平均は読み取れない。
エ・・誤。生徒の人数が15人だから、中央値は小さい方から8番目の記録である。中央値は57回だから、小さい方から8番目の記録は57回である。
第3四分位数は60回より大きく70回より小さいから、小さい方から9番目の記録が61回以上のことも考えられ、このとき、60回以下の生徒は8人となる。
オ・・正。第3四分位数は、記録の大きい方7人の中央値だから、大きい方から4番目の記録である。第3四分位数は60回より大きく70回より小さいので、大きい方から4番目の記録は60回より大きい。よって、60回以上の生徒は4人以上いる。
大問2 関数
問題文
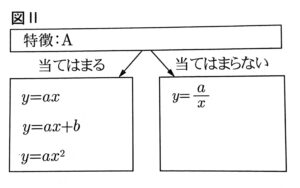
yがxの関数である4つの式$y=ax,y=\frac{a}{x},y=ax+b,y=ax^2$について、aとbが0でない定数のとき、下の例のように、ある特徴に当てはまるか当てはまらないかを考え、グループ分けする。次の（1）（2）の問いに答えなさい。
（1）図1のように、特徴を「変化の割合は一定である」とするとき、次の①、②の式は、どちらにグループ分けできるか。当てはまるグループの場合は〇を、当てはまらないグループの場合は×を書きなさい。
①$y=ax+b$ ②$y=ax^2$
（2）次のア～エのうち、図2の特徴であるAとして適切なものをすべて選び、記号で答えなさい。
ア グラフはy軸について対称である
イ グラフはy軸と交点をもつ
ウ x=1のとき、y=aである
エ a>0でx>0のとき、xが増加するとyも増加する
解答・解説
（1）① ○ ② ×
① 関数$y = ax + b$は一次関数だから、変化の割合は一定である。
② 変化の割合は一定ではない。
（2）イ、エ
ア. $y$軸について対称なグラフは、関数$y = ax^2$のグラフのみである。
ウ. 関数$y = ax + b$は$x = 1$ の時$y = a + b$である。$b$は0でないので、$y = a$ではない。
0120-740-100
LINE問合せ窓口
LINEからもお問合せいただけます！
公式Instagram
勉強のお役立ち情報を配信中！
お問い合わせ、ご質問も受付中です！
ご質問などお気軽にお問い合わせください。
大問3 規則性を問う問題
問題文
ある整数a,bと5が、次のようにaを1番目として左から規則的に並んでいる。このとき、あとの（1）（2）の問いに答えなさい。
【a,5,b,a,5,b,a,5,b,a,…】
（1）20番目の整数は、a,b,5のうちどれか、答えなさい。
（2）1番目から7番目までの整数の和が18、1番目から50番目までの整数の和が121であるとき、aとbの値をそれぞれ求めなさい。
ただし、答えを求める過程を書くこと。
解答・解説
（1）5
a, 5, b の 3 つの整数がこの順に繰り返して並んでいる。
20÷3=6 あまり2より、20番目までは、a,5,b の 3 つの整数が6回繰り返して並んだ後に、a、5の2つの整数が並ぶので、20番目の整数は5である。
（2）a = 4,、b = -2
1番目から7番目までは「a,5,b,a,5,b,a」だから、その和が18より、a+5+b+a+5+b+a=18 が成り立ち、3a+2b=8…①となる。
また、50÷3=16あまり2より、50番目までは a,5,b の3つの整数が 16 回繰り返して並んだ後に、a、5の2つの整数が並ぶ。
その和が 121 より、(a+5+b)×16+a+5=121 が成り立ち、17a+16b=36…②となる。
①②の連立方程式を解くと、①×8-②より、
24a-17a=64-36
7a=28
a=4
となり、これを①に代入して、
3×4+2b=8
2b=-4
b=-2となる。
大問4 図形
問題文
南さんは、平行四辺形の学習を振り返り、次のように図形の性質に関わる【ことがら】をまとめた。後の（1）（2）の問いに答えなさい。
【ことがら】
四角形ABCDが平行四辺形ならば、
四角形ABCDの対角線BDによってつくられる2つの三角形は合同である。
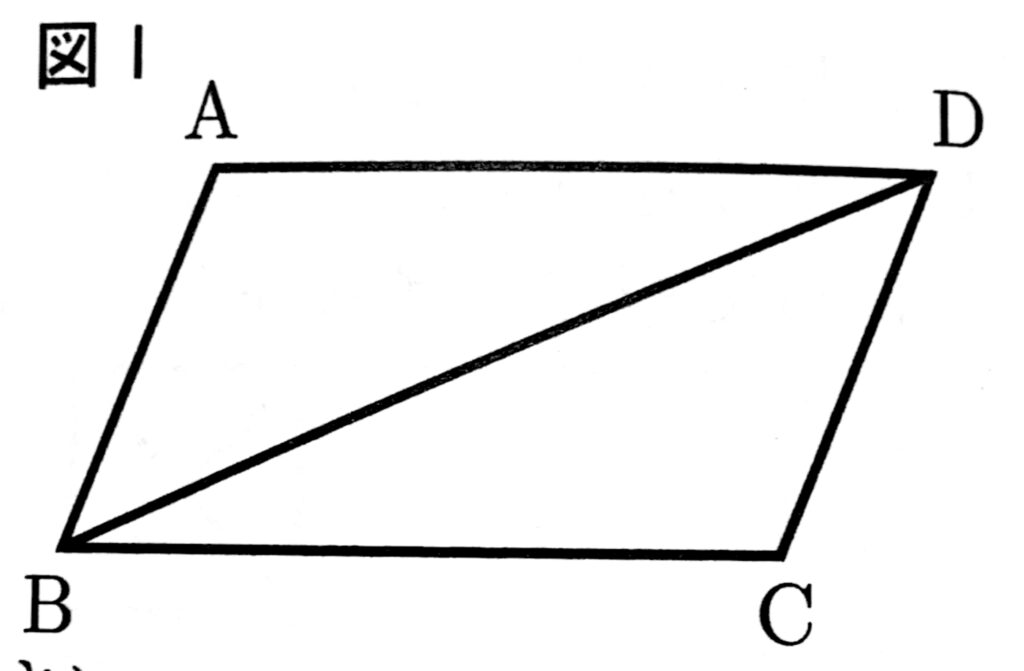
（1）南さんがまとめた【ことがら】が成り立つことを示したい。図1において、四角形ABCDが平行四辺形のとき、三角形ABDと三角形CDBが合同になることを証明しなさい。
（2）南さんは自分がまとめた【ことがらの逆】は成り立たないことに気づいた。
【ことがらの逆】
四角形ABCDの対角線BDによって作られる2つの三角形が合同ならば、
四角形ABCDは平行四辺形である。
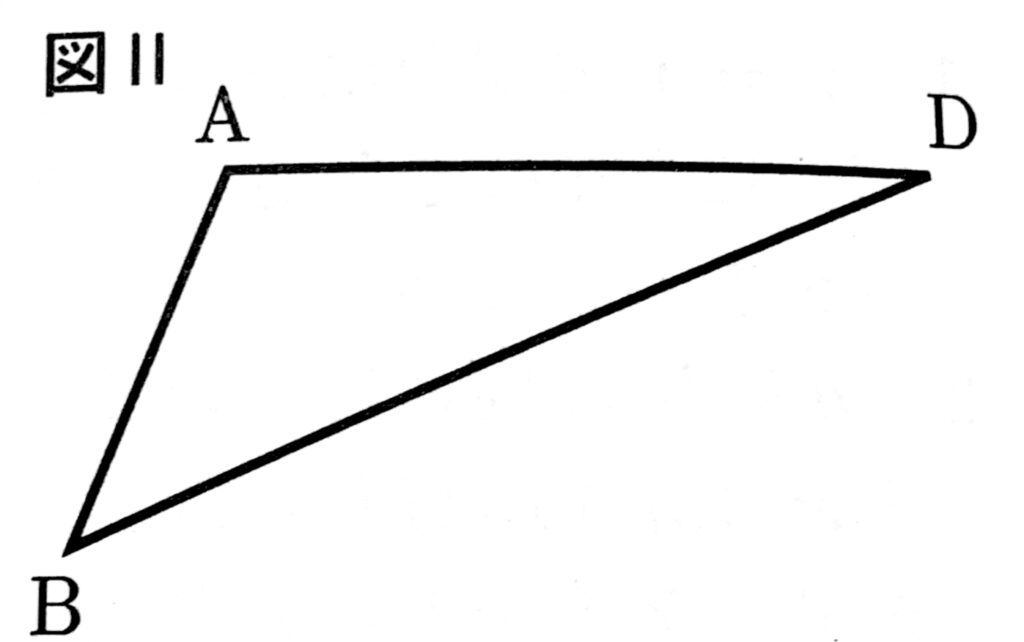
図2において【ことがらの逆】の反例となる四角形ABCDを完成させるよう、線分BCと線分CDを、コンパスと定規を用いて作図しなさい。
ただし、作図に用いた線は消さないこと。
解答・解説
（1）
(例) △ABDと△CDBにおいて、共通な辺より、
BD=DB・・・①
平行四辺形の対辺は等しいから、
AB=CD・・・②
AD=CB・・・③
①、②、③より、3組の辺がそれぞれ等しいから、
△ABD≡△CDB
(2)
対角線BDによって、△ABD≡△CBDとなる四角形ABCDを考える。このとき、対応する辺より、BA=BC,、DA=DCである。
よって、作図は、まず、①点Bを中心とする半径BAの円の弧をかき、②点Dを中心とする半径DAの円の弧をかく。
①と②の交点のうち、点Aでない方が点Cとなる。
③点Bと点C、点Cと点Dをそれぞれ結ぶ。
LINE問合せ窓口
LINEからもお問合せいただけます！
公式Instagram
勉強のお役立ち情報を配信中！
お問い合わせ、ご質問も受付中です！
ご質問などお気軽にお問い合わせください。
大問5 関数
問題文
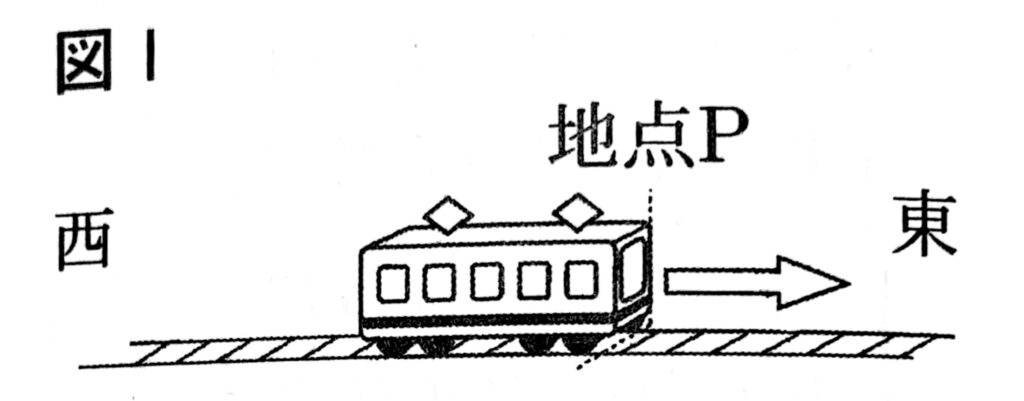
図1のように地点Pに止まっていた電車が、東西にますぐな線路を走り始めた。電車が出発してからx秒後までに地点Pから東に進んだ距離をyｍとすると、20秒後までは$y=\frac{1}{4}x^2$の関係がある。このとき、次の（1）（2）の問いに答えなさい。
ただし、電車の位置は、その先端を基準に考えるものとする。
（1）電車は出発してから6秒後までに東の方向へ何m進んだか、求めなさい。
（2）図2のように、和也さんは線路と平行に走る道を東に向かって毎秒$\frac{10}{3}$ｍの速さで走っている。電車が地点Pを出発した時に、和也さんが地点Pより西にある地点Qを通過し、その10秒後に電車と和也さんが同じ地点を走っていた。
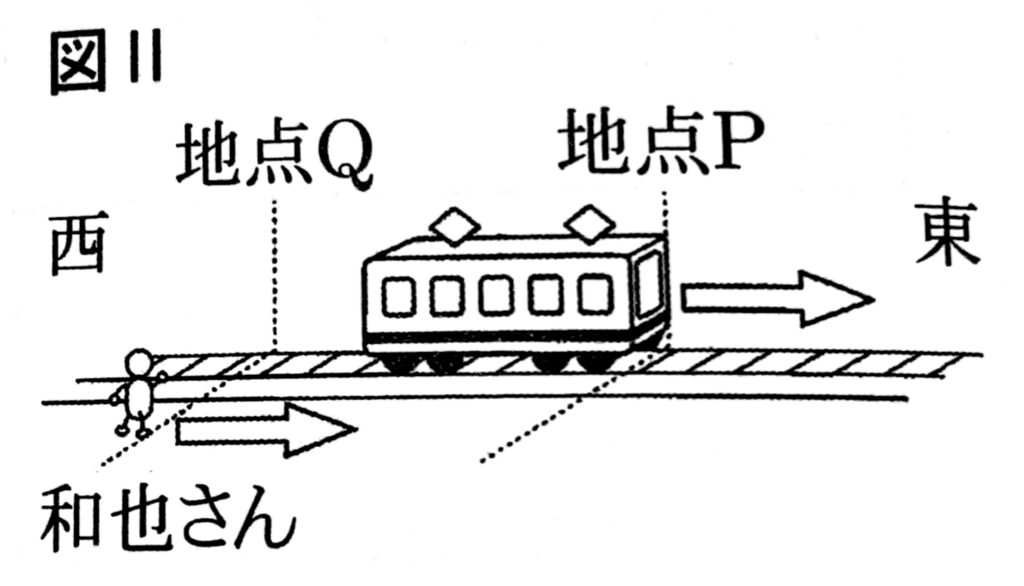
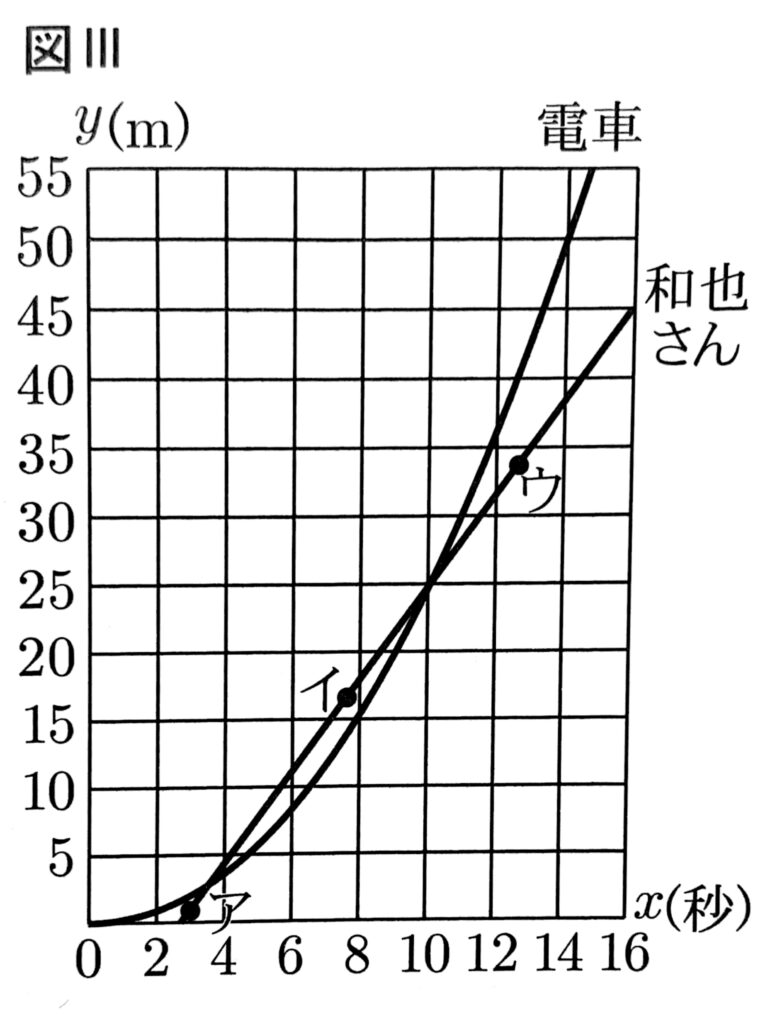
図3が、電車が出発してからx秒後までに地点Pから東に進んだ距離をyｍとして、電車と和也さんが地点Pより東を走るときのxとyの関係を表したグラフであるとき、次の①～③の問いに答えなさい。
① 図3のグラフ上にある点ア～ウのうち、和也さんが電車より前を走っていることを表す点を1つ選び、記号で答えなさい。
② 地点Qから地点Pまでの距離を求めなさい。
③ 和也さんが地点Pを走っていたときの、和也さんと電車との距離を求めなさい。
解答・解説
（1）9m
電車が出発してから $x$ 秒後までに進んだ距離$y$mは、20 秒後までは$y=\frac{1}{4}x^2$と表せるから、6 秒後までに進んだ距離は、$y=\frac{1}{4}x^2$に$x=6$を代入して、$y=\frac{1}{4} \times 6^2 = 9$(m)となる。
（2）① イ ② $\frac{25}{3}$m ③ $\frac{25}{16}$m
① 和也さんが電車より前を走っているとき、電車よりも地点 P から東に進んだ距離が長くなるから、電車と和也さんのグラフで、同じ x の値のときの y の値は和也さんの方が大きくなる。これを満たす点はイである。
② 電車が地点 P を出発したとき、和也さんは地点 Q を通過し、その 10 秒後に電車と和也さんは同じ地点を走っていたので、10 秒後に走っている地点は、地点 P から、25m 進んだ地点である。
和也さんは毎秒$\frac{10}{3}$mで走っているので、地点 Q から、$\frac{10}{3} \times 10 = \frac{100}{3}$(m)進んでいる。よって地点 Q から地点 P までの距離は、$\frac{100}{3} – 25 = \frac{25}{3}$(m)となる。
③ ②より、地点 Q から地点 P までの距離は、$\frac{100}{3} – 25 = \frac{25}{3}$(m)だから、和也さんは、地点 Q から地点 P まで、$\frac{25}{3} \div \frac{10}{3} = \frac{5}{2}$(秒)かかる。
よって、和也さんが地点 P を走っているのは、電車が地点 P を出発してから$\frac{5}{2}$秒後である。この時、地点 P から電車が進んだ距離は、$y=\frac{1}{4} \times (\frac{5}{2})^2 = \frac{25}{16}$(m)だから、和也さんと電車の距離は$\frac{25}{16}$mである。
大問6 図形
問題文
次の図のように、線分ABを直径とする円Oと、線分OA上の点Cを中心として、線分COを半径とする円Cとが交わるとき、その交点をD,D’とする。また、半直線DO,DCと円Oとの交点をそれぞれE,Fとする。次の（1）（2）の問いに答えなさい。
（1）∠AOD＝$\frac{1}{2}$∠EOFとなることをつぎのように説明した。【ア】、【ウ】には適する語を、【イ】には適する記号をそれぞれ入れなさい。
ただし、弧EFは、円周上の2点E,Fをそれぞれ両端とする弧のうち長くない方を表すものとする。
説明
円Cの半径より、CO＝CDだから、△CODは【ア】三角形になるので。
∠EDF＝∠【イ】…①
また、∠EDFは弧EFの円周角であり、円周角は【ウ】角の$\frac{1}{2}$倍になるので、
∠EDF＝$\frac{1}{2}$∠EOF…②
したがって、①、②より
∠AOD＝$\frac{1}{2}$∠EOFになる。
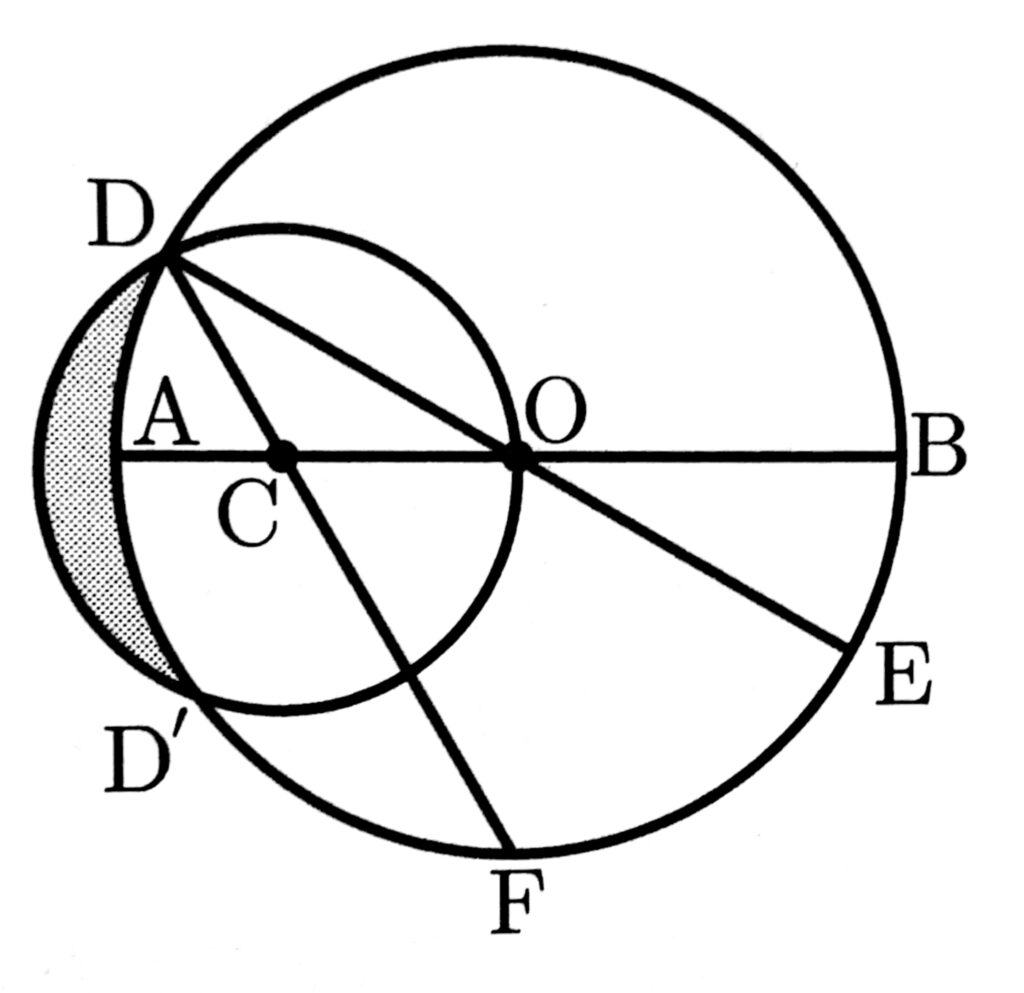
（2）AB＝12ｃｍ、∠BOF＝90°のとき、次の①～③の問いに答えなさい。
① ∠EDFの大きさを求めなさい。
② COの長さを求めなさい。
③ 図において色をつけて示した、円Cのうち円Oと重なっていない部分の面積を求めなさい。
ただし、円周率はπとする。
解答・解説
（1）ア：ニ等辺 イ：AOD ウ：中心
上図1で CO=CD だから、$\triangle\text{COD}$は二等辺三角形である。よって底角は等しい。また、$\angle\text{EDF}=\frac{1}{2}\angle\text{EOF}$から、$\angle\text{AOD}=\frac{1}{2}\angle\text{EOF}$ を導いているから、$\angle\text{EDF}=\angle\text{AOD}$ である。また弧EFに対する円周角は中心角の$\frac{1}{2}$倍であることから導いている。
（2）① $30^\circ$ ② $2\sqrt{3}$cm ③ $6\sqrt{3}-2\pi$ cm$^2$
① 対頂角より$\angle\text{AOD}=\angle\text{BOE}$ である。また (1) より$\angle\text{AOD}=\frac{1}{2}\angle\text{EOF}$ だから、$\angle\text{EOF}=2\angle\text{AOD}$ である。
よって、$\angle\text{BOF}=\angle\text{EOF}+\angle\text{BOE}=2\angle\text{AOD}+\angle\text{AOD}=3\angle\text{AOD}$ である。$\angle\text{BOF}=90^\circ$より、$\angle\text{AOD}=30^\circ$となる。$\triangle\text{COD}$はCO=CDの二等辺三角形だから、$\angle\text{EDF}=\angle\text{AOD}=30^\circ$となる。
② 図1のように、点Cから線分ODに垂線CHを引くと、$\triangle\text{COD}$はCO=CDの二等辺三角形だから、点Hは線分ODの中点となる。OD=OA=$\frac{1}{2}$AB=6だから、OH=3となる。また、$\triangle\text{OCH}$は$1:2:\sqrt{3}$の直角三角形となる。よって CO=$2\sqrt{3}$(cm)
③ $4\pi+3\sqrt{3}+3\sqrt{3}-6\pi=6\sqrt{3}-2\pi$ (cm$^2$)
円Cのうち円Oと重なっていない部分の面積は、{おうぎ形 CDD+ACOD+ACOD}-{おうぎ形 ODD}で求められる。
CD=CD,CO=CO, OD=OD, より、$\triangle\text{COD}=\triangle\text{COD}$ であるから、$\angle\text{AOD}=\angle\text{AOD’}$であり、$\angle\text{DOD’}=2\angle\text{AOD}=2\times30^\circ=60^\circ$となる。また、円Cの弧DD’に対する円周角と中心角の関係より、$\angle\text{DCD’}=2\angle\text{DOD’}=2\times60^\circ=120^\circ$となる。
よって、CD=CO=$2\sqrt{3}$より、求める面積は、$4\pi+3\sqrt{3}+3\sqrt{3}-6\pi=6\sqrt{3}-2\pi$ (cm$^2$)である。
志望校に合わせた受験対策なら、やる気アシストにお任せ下さい！
家庭教師のやる気アシストは、群馬県にお住まいの受験生のお子さんを毎年たくさん指導をさせ頂き、合格に導いています。
高い合格率の秘訣は、指導経験豊富な先生の指導力に加え、1対1の指導でお子さん一人ひとりの状況に合わせた、お子さんだけのカリキュラムで勉強が進められるから！
家庭教師のやる気アシストは、お子さんの志望校合格まで全力でサポートさせて頂きます！
LINE問合せ窓口
LINEからもお問合せいただけます！
公式Instagram
勉強のお役立ち情報を配信中！
お問い合わせ、ご質問も受付中です！
ご質問などお気軽にお問い合わせください。
アシストの指導方法がじっくり見れる！知れる！無料の体験授業実施中
お子さんにとって「成果が出る勉強法」ってどんな勉強法だと思いますか？
お子さんそれぞれに、個性や性格、学力の差もあります。そんな十人十色のお子さん全員に合う勉強法ってなかなかないんです。
たからこそ、受験生の今だけでもお子さんだけの勉強法で受験を乗り越えてみませんか？
やる気アシストには、決まったカリキュラムはありません。お子さんの希望や学力、得意や不得意に合わせて、お子さんだけのカリキュラムで指導を行っていきます。また、勉強法もお子さんそれぞれに合う合わないがあります。無料体験授業では、お子さんの性格や生活スタイルを見せていただき、お子さんにとって効率的な成果の出る勉強のやり方をご提案させて頂きます。
