【静岡県】令和5年度/2023年度入学者高校入試選抜試験：数学の解説
静岡県の2023年3月実施の令和5年度（2023年度）入学者の公立高校入試問題の解説をしています。
受験勉強において、過去問を解くことはとても効果的な勉強法です。ぜひ、受験までに一度挑戦し、問題の傾向を掴んでおきましょう。合わせて、対策などをたてられるととても良いですね。
また、過去問で苦手な点が見つかった場合は、そこを中心に試験日当日までにしっかりと対策しておきましょう。
大問1 小問集合
問題文
次の（1）～（3）の問いに答えなさい。
（1）次の計算をしなさい。
ア $-8+27\div(-9)$
イ $(-6a)^2\times 9b \div 12ab$
ウ $\frac{2x+y}{3}-\frac{x+5y}{7}$
エ $\sqrt{45}+\frac{10}{\sqrt{5}}$
（2）$a=41,b=8$のとき、$a^2-25b^2$の式の値を求めなさい。
（3）次の２次方程式を解きなさい。
$x^2+7x=2x+24$
解答・解説
（1）
ア -11
$-8+27 \div (-9) = -8-3 = -11$
イ $27a$
$(-6a)^2 \times 9a \div 12ab = \frac{36a^2 \times 9a}{12ab} = 27a$
ウ $\frac{11x-8y}{21}$
$\frac{2x+y}{3} – \frac{x+5y}{7} = \frac{7(2x+y)-3(x+5y)}{21} = \frac{14x+7y-3x-15y}{21} = \frac{11x-8y}{21}$
エ $5\sqrt{5}$
$\sqrt{45}+\frac{10}{\sqrt{5}} = 3\sqrt{5}+\frac{10\sqrt{5}}{5} = 3\sqrt{5}+2\sqrt{5}=5\sqrt{5}$
（2） $a^2-25b^2 = (a+5b)(a-5b) = (41+40)(41-40) = 81$
（3）$x=3, -8$
$x^2+7x=2x+24$
$x^2+5x-24=0$
$(x+8)(x-3)=0 \quad \therefore x=3, -8$
大問2 作図と確率
問題文
次の（1）～（3）の問いに答えなさい。
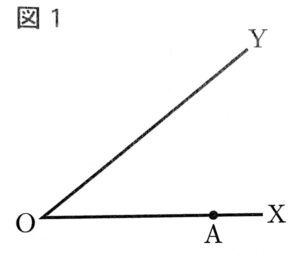
（1）図1において、点Aは辺OX上の点である。点Aから辺OYに引いた垂線上にあり、2辺OX,OYから等しい距離にある点Pを作図に用いた線は残しておくこと。
（2）次の【 】の中に示したことがらの逆を書きなさい。
【aもbも正の数ならば、a+bは正の数である。】
また、【 】の中のことがらは正しいが、逆は正しくない。【 】の中のことがらの逆が正しくないことを示すための反例を、1つ書きなさい。
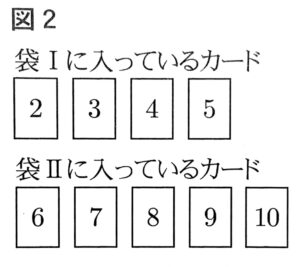
（3）2つの袋Ⅰ、Ⅱがあり、袋Ⅰには2，3，4，5の数字を1つずつ書いた4枚のカードが、袋Ⅱには6，7，8，9，10の数字を1つずつ書いた5枚のカードが入っている。図2は、袋Ⅰと袋Ⅱに入っているカードを示したものである。
2つの袋Ⅰ、Ⅱから、それぞれ1枚のカードを取り出すとき、袋Ⅱから取り出したカードに書いてある数が、袋Ⅰから取り出したカードに書いてある数の倍数である確率を求めなさい。ただし、袋Ⅰからカードを取り出すとき、どのカードが取り出されることも同様に確からしいものとする。また袋Ⅱについても同じように考えるものとする。
解答・解説
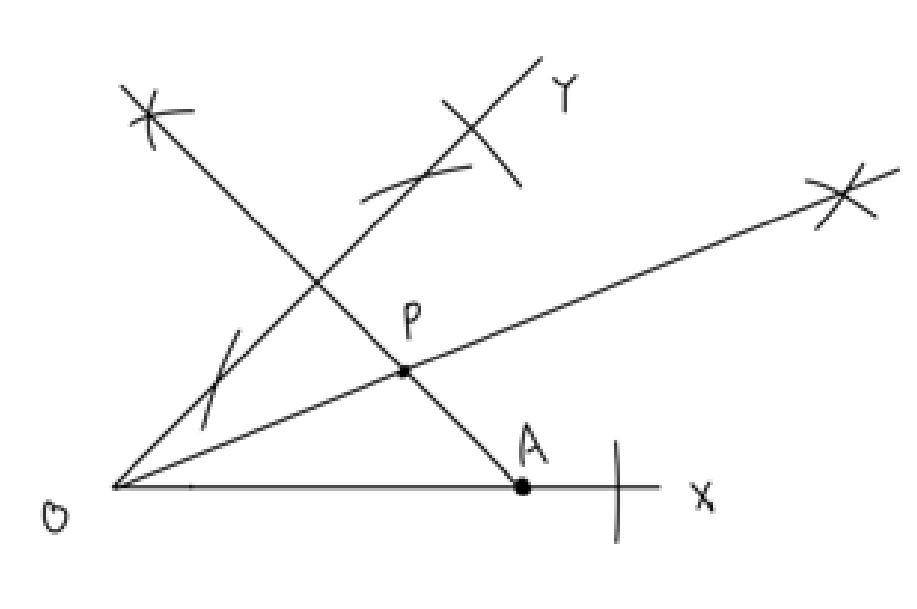
（1）図の通り
点Aから半直線OYに引いた垂線と∠XOYの二等分線の交点を作図する。
（2）逆：$a+b$が正の数ならば、$a$も$b$も正の数である。反例：$a=-1, b=2$
実際、$a+b=1$は正だが、$a$は正ではない。
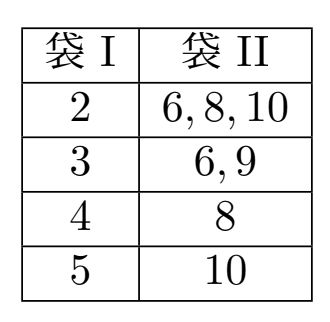
（3）$\frac{7}{20}$
題意を満たす取り出し方は以下の$3+2+1+1=7$通り。
取り出し方は全部で$4 \times 5 = 20$通りあるので、求める確率は$\frac{7}{20}$
0120-740-100
LINE問合せ窓口
LINEからもお問合せいただけます！
公式Instagram
勉強のお役立ち情報を配信中！
お問い合わせ、ご質問も受付中です！
ご質問などお気軽にお問い合わせください。
大問3 資料の活用
問題文
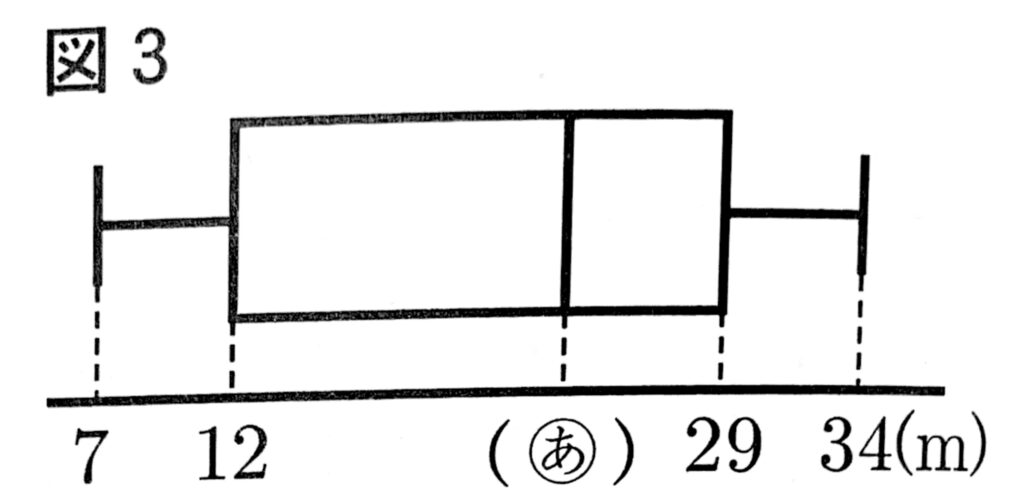
あるクラスの10人の生徒A～Jが、ハンドボール投げを行った。表1は、その記録を表したものである。図3は、表1の記録を箱ひげ図に表したものである。
このとき、次の（1）、（2）の問いに答えなさい。
（1）図3の【あ】に適切な値を補いなさい。また、10人の生徒A～Jの記録の四分位範囲を求めなさい。
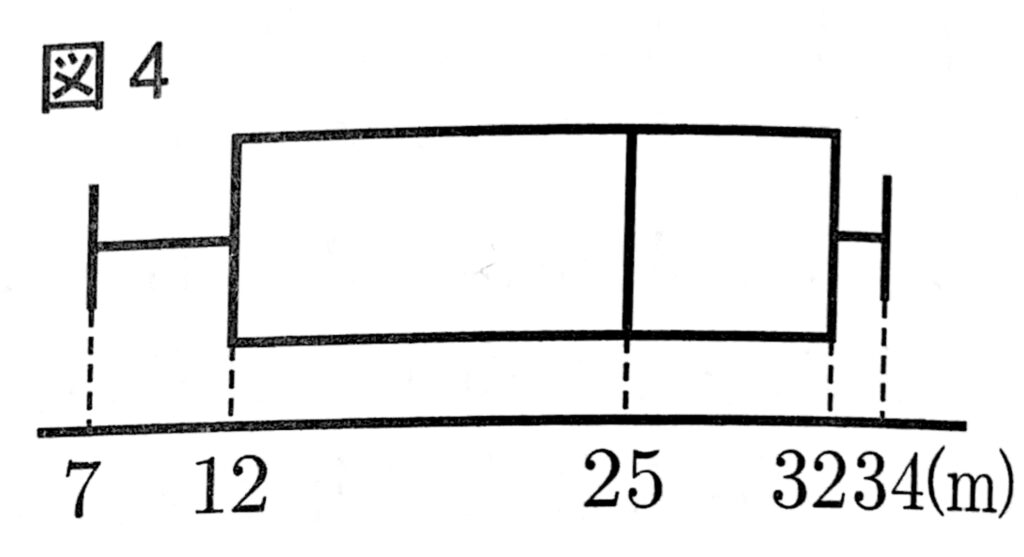
（2）後日、生徒Kもハンドボール投げをおこなったところ、Kの記録はamだった。図4は、11人の生徒A～Kの記録を箱ひげ図に表したものである。
このとき、aがとりうる値をすべて求めなさい。ただし、aは整数とする。
解答・解説
生徒A～Jの記録を昇順に並べると、図のようになる。
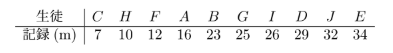
（1）【ア】24 【四分位範囲】17
◎は中央値を表す。生徒は10人(偶数)なので、中央値は中央の2つの値を平均して求める。
$\frac{23+25}{2}=24$
四分位範囲は、第３四分位数から第１四分位数を引いて求める。
$29-12=17$
（2）$a=32,33,34$
中央値が25、第3四分位数が32に変わっていることに注意。生徒の人数は11人となるので、中央値は下から6番目の値、第3四分位数は下から9番目の値となる。生徒Kを除く10人の記録のうち、下から9番目の記録は生徒Jの32mである。
$a<32$であると仮定しよう。このとき、下から9番目の記録は$a \le 29$なら生徒Dの29m(あるいは、$a > 29$なら生徒Kのa[m])となる。しかし第3四分位数は32であるので、矛盾する。
従って$a \ge 32$である。
最大値が34mであるため、$32 \le a \le 34$ が従う。この不等式を満たす整数$a$は32,33,34の3通りであり、実際にこれらは与えられた箱ひげ図を実現することが容易に確かめられる。
よって、$a=32,33,34$
大問4 連立方程式
問題文
ある中学校の生徒会が,ボランティア活動で, 鉛筆とボールペンを集め、 2つの団体S, Tへ送ることにした。 団体Sは鉛筆のみを, 団体Tは鉛筆とボールペンの両方を受け付けていた。
この活動で,鉛筆はボールペンの2倍の本数を集めることができた。鉛筆については,集めた本数の80%を団体 Sへ、残りを団体 Tへ送った。また, ボールペンについては、集めた本数の4%はインクが出なかったため,それらを除いた残りを団体 Tへ送った。 団体 Tへ送った, 鉛筆とボールペンの本数の合計は、団体S へ送った鉛筆の本数よりも18本少なかった。
このとき、集めた鉛筆の本数とボールペンの本数は, それぞれ何本であったか。 方程式をつくり, 計算の過程を書き,答えを求めなさい。
解答・解説
集めた鉛筆とボールペンの本数をそれぞれ$x$本、$y$本とする。鉛筆はボールペンの2倍の本数を集めたので$x=2y \cdots(1)$
団体S, Tに送られた鉛筆とボールペンの本数を表にして整理しよう。
まず鉛筆については、集めた本数のうち80%を団体Sへ、残り20%を団体Tへ送る。
よって、ア $=\frac{4}{5}x$, イ $=\frac{1}{5}x$
| 団体S | 団体T | |
| 鉛筆 | ア | イ |
| ボールペン | ウ | エ |
ボールペンについては、団体Sは受け付けていないため、ウ=0
団体Tに送るボールペンの本数は、集めた本数のうちインクの出なかった4%を除いた96%であるので、エ $=\frac{96}{100}y = \frac{24}{25}y$
よって、表は次のようになる。
| 団体S | 団体T | |
| 鉛筆 | $=\frac{4}{5}x$ | $=\frac{1}{5}x$ |
| ボールペン | 0 | $\frac{24}{25}y$ |
ここで、団体Tに送った鉛筆とボールペンの本数の合計は、団体Sに送った鉛筆の数よりも18本少ないので、$\frac{1}{5}x + \frac{24}{25}y = \frac{4}{5}x – 18$
両辺を整理すると、$\frac{3}{5}x – \frac{24}{25}y = 18$
両辺に$\frac{25}{3}$をかけて、$5x – 8y = 150 \cdots(2)$
(1)(2)を連立方程式として解こう。(1)式 $x=2y$を(2)式に代入すると、
$5 \cdot 2y – 8y = 150 \implies 10y – 8y = 150 \implies 2y = 150 \implies y=75$
よって、$x=2y=150$
以上より、集めた鉛筆の本数$x$とボールペンの本数$y$はそれぞれ、$x=150$本、$y=75$本
LINE問合せ窓口
LINEからもお問合せいただけます！
公式Instagram
勉強のお役立ち情報を配信中！
お問い合わせ、ご質問も受付中です！
ご質問などお気軽にお問い合わせください。
大問5 空間図形
問題文
図5の立体は、円Oを底面とする円すいである。この円すいにおいて、底面の半径は3ｃｍ、母線ABの長さは6cmである。また、線分OAと底面は垂直である。
このとき（1）～（3）の問いに答えなさい。
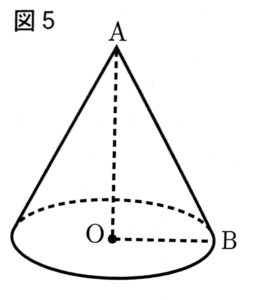
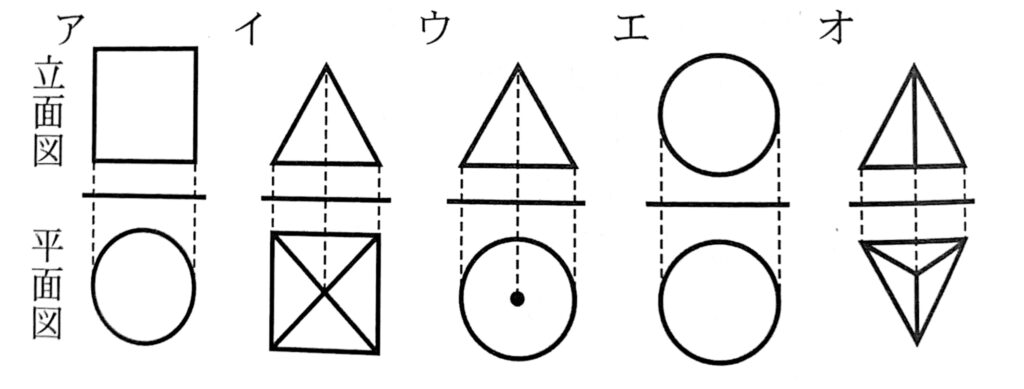
（1）次のア～オの5つの投影図のうち、1つは円すいの投影図である。円すいの投影図を、ア～オの中から1つ選び、記号で答えなさい。
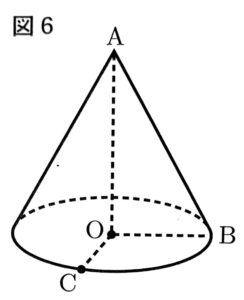
（2）この円すいにおいて、図6のように、円Oの円周上に∠BOC＝110°となる点Cをとる。小さいほうの弧BCの長さを求めなさい。ただし、円周率はπとする。
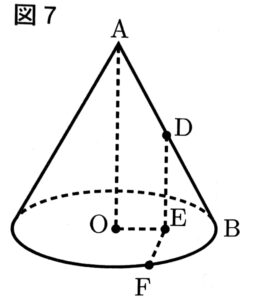
（3）この円すいにおいて、図7のように、ABの中点をDとし、点Dから底面に引いた垂線と底面の交点をEとする。また、円Oの円周上に∠OEF＝90°となる点Fをとる。△ODFの面積を求めなさい。
解答・解説
（1）ウ
円すいは、正面から見ると二等辺三角形であり、上から見ると円である。よってウ。
（2） $\frac{11}{6}\pi$[cm]
底面の半径は3cmなので、弧BCの長さは、$2\pi \cdot 3 \cdot \frac{11}{360} = \frac{11}{6}\pi$[cm]
（3）$\frac{9\sqrt{15}}{8} [\text{cm}^2]$
まず$\triangle AOB$に注目する。$AO // DE$より、点Eは辺OBの中点である。よって、$\triangle DEB \equiv \triangle DEO$である（DE共通, BE=OE, $\angle DEB=\angle DEO=90^\circ$より二辺夾角相等）。これにより、$OD=BD=3$となる。
【注】ODの長さについては、別の方法で求めることもできる。$\triangle AOB$の外接円を考えると、$\angle AOB=90^\circ$よりABはその外接円の直径であり、中心はその中点Dである。外接円の半径はAD=BD=3なので、半径ODの長さもまた3である。
また、$AB=6, OB=3$より、$\triangle AOB$は辺の比が$1:2:\sqrt{3}$の直角三角形である。よって、$AO=3\sqrt{3}$であり、中点連結定理より$DE=\frac{3\sqrt{3}}{2}$が導かれる。
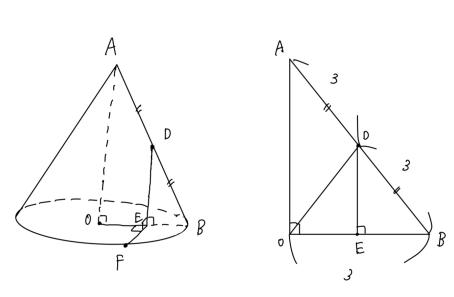
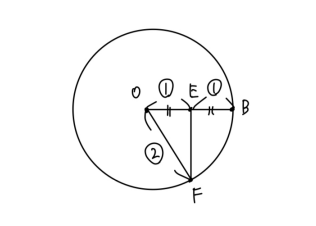
次は底面に注目する。点Eは辺OBの中点であるので、図のようにして$\triangle OEF$が辺の比が$1:2:\sqrt{3}$の直角三角形であることが分かる。
$OF=3$より、$EF = \frac{3\sqrt{3}}{2}$である。
$\angle DEF=90^\circ$, $DE=\frac{3\sqrt{3}}{2}$より、$\triangle DEF$は辺の比が$1:1:\sqrt{2}$の直角二等辺三角形である。
よって、$DF=\sqrt{2} \cdot \frac{3\sqrt{3}}{2} = \frac{3\sqrt{6}}{2}$である。
以上により、$\triangle ODF$の3辺の長さがすべて求まった。
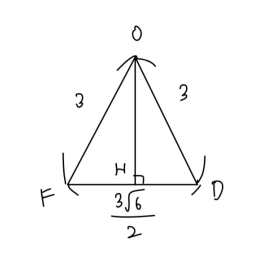
$\triangle ODF$の面積を求める。$\triangle ODF$は二等辺三角形であることに注意する。
点Oから辺DFに引いた垂線の足をHとおく。
$DH = \frac{1}{2}DF = \frac{1}{2}\frac{3\sqrt{6}}{2} = \frac{3\sqrt{6}}{4}$である。
$\triangle ODH$に三平方の定理を適用して、
$OH^2 = OD^2 – DH^2 = 3^2 – (\frac{3\sqrt{6}}{4})^2 = 9 – \frac{54}{16} = 9 – \frac{27}{8} = \frac{45}{8}$
すなわち、$OH=\sqrt{\frac{45}{8}}=\frac{3\sqrt{10}}{4}$である。
よって、$\triangle ODF$の面積は、$\frac{1}{2}\cdot DF \cdot OH = \frac{1}{2} \cdot \frac{3\sqrt{6}}{2} \cdot \frac{3\sqrt{10}}{4} = \frac{9\sqrt{15}}{8} [\text{cm}^2]$
大問6 二次関数
問題文
次の文は、授業でT先生が示した資料である。このとき、次の（1）～（3）の問いに答えなさい。
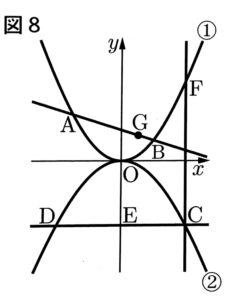
図8において、➀は関数$y=ax^2(a>0)$グラフであり、②は関数$y=bx^2(b<0)$のグラフである。2点A,Bは、放物線➀上の点であり、そのx座標は、それぞれ-3，2である。
点Cは、放物線②の上の点であり、その座標は（4，-4）である。点Cを通りx軸に平行な直線と放物線②との交点をDとし、直線CDとy軸の交点をEとする。
点Cを通り、y軸に平行な直線と放物線➀との交点をFとする。また、点Gは直線AB上の点であり、そのx座標は1である。
RさんとSさんは、タブレット型端末を使いながら、図8のグラフについて話している。
Rさん：関数$y=bx^2$の比例定数bの値は求められるね。
Sさん：②は点Cを通るからbの値は【あ】だよ。
Rさん：関数$y=ax^2$のaの値は決まらないね。
Sさん：タブレット型端末を使うと㋐aの値を変化させたときのグラフや図形の変化するようすが分かるよ。
Rさん：そうだね。㋑3点D,G,Fが一直線上にある場合もあるよ。
Sさん：本当だね。計算で確認してみよう。
（1）【あ】に適切な値を補いなさい。
（2）下線部㋐のときの、グラフや図形の変化のようすについて述べたものとして正しいものを、次のア～オの中からすべて選び、記号で答えなさい。
ア aの値を大きくすると、➀のグラフの開き方は小さくなる。
イ aの値を小さくすると、点Aのy座標から点Bのy座標を引いた値は大きくなる。
ウ aの値を大きくすると、△OBEの面積は大きくなる。
エ aの値を小さくすると、直線OBの傾きは小さくなる。
オ aの値を大きくすると、線分CFの長さは短くなる。
（3）下線部㋑のときの、aの値を求めなさい。求める過程も書きなさい。
解答・解説
（1）$b = -\frac{1}{4}$
放物線 $y=bx^2$ は点 C(4, -4)を通るので、
$-4 = b \cdot 4^2 = 16b$
したがって、$b = -\frac{1}{4}$
（2）ア、エ
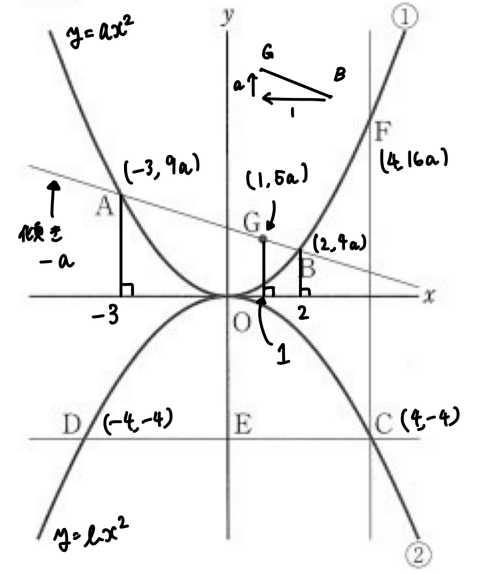
各点の座標を求めよう。
点 A, B, F は放物線 $y=ax^2$ 上の点である。
点 A, B, F の $x$ 座標はそれぞれ -3, 2, 4 なので、その $y$ 座標は$(-3)^2a=9a$, $2^2a=4a$, $4^2a=16a$である。
よって、A(-3, 9a), B(2, 4a), F(4, 16a)と座標が求まる。
また、点Dの座標は対称性より (-4, -4) である。
直線 AB の傾きは$\frac{4a-9a}{2-(-3)} = \frac{-5a}{5} = -a$
ゆえに、点 G の $y$ 座標は $\frac{y-4a}{1-2} = -a$ の解である（点 G から点 B への変化の割合が直線 AB の傾きに等しい）。
よって、点 G の座標は (1, 5a) となる。
これらを踏まえ、ア～オの正誤を調べる。
ア：正しい。一般に放物線 $y=ax^2(a>0)$ のグラフは、$a$が大きくなればなるほど開き方が小さくなる。
イ：誤り。点Aの$y$座標から点Bの$y$座標を引いた値は $9a-4a=5a$ である。$a$の値を小さくすると、この値は小さくなる。
ウ：誤り。$\triangle OBE$の面積は一定である。実際、底辺OEの長さを4、高さを点Bの$y$座標3とすると、$\triangle OBE = \frac{1}{2}\cdot4\cdot3=6$
エ：正しい。直線OBの傾きは $\frac{4a}{2}=2a$ である$a$の値を小さくすると、この値は小さくなる。
オ：誤り。CFの長さはFの$y$座標からCの$y$座標を引いた値、$16a-(-4)=16a+4$である。$a$を大きくすると、この値は大きくなる。
（3）$\frac{3}{10}$
3点D, G, Fが一直線上にあることと、直線DGと直線GFの傾きが等しいことは同値である。これを用いて$a$の値を求める。
直線DGの傾きは、$\frac{5a-(-4)}{1-(-4)} = \frac{5a+4}{5}$
直線GFの傾きは、$\frac{16a-5a}{4-1} = \frac{11a}{3}$
よって、$\frac{5a+4}{5} = \frac{11a}{3}$
両辺に15を掛けると、$15a+12=55a \implies 40a=12 \implies a=\frac{3}{10}$
$a$の値が求まる。
大問7 平面図形
問題文
図9において、4点A,B,C,Dは円Oの円周上の点である、△ABCはBA＝BCの二等辺三角形である。ACとBDとの交点をEとし、点Eを通りADに平行な直線とCDとの交点をFとする。またBD上にGC＝GDとなる点Gをとる。
このとき、次の（1）（2）の問いに答えなさい。
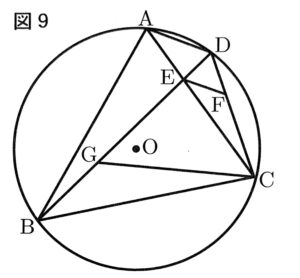
（1）△BCG∽△ECFであることを証明しなさい。
（2）GC＝4ｃｍ、BD＝6ｃｍ、CF＝2ｃｍのとき、GEの長さを求めなさい。
解答・解説
（1）
$a=b$ (円周角の定理)
$=c$ (AD//EF, 同位角) $\cdots$ ア
また、
$f=g$ (BC=BA)
$=h$ (円周角の定理)
$=i$ (GD=GC)
ゆえに、
$d=f-\angle ECG = i-\angle ECG = c \cdots$ イ
アとイより二角相等で $\triangle BCG \backsim \triangle ECF$ が従う。
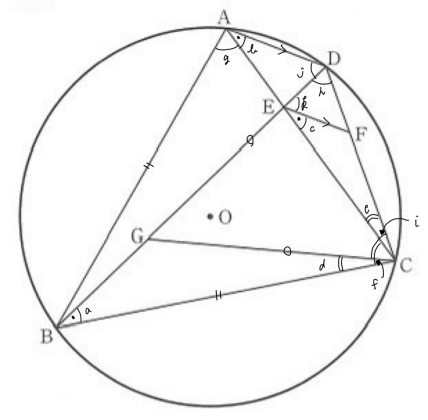
（2）$\frac{13}{4}$ cm
$k=j$ (AD//EF, 錯角)
$=f$ (円周角の定理)
$=g$ (BC=BA)
$=h$ (円周角の定理)
よって、$\triangle DEF$は$FD=FE$の二等辺三角形となる。$\cdots$ ウ
また、(1)より $\triangle BCG \backsim \triangle ECF$ であるが、相似比は$GC:FC=4:2=2:1$
$GD=GC=4$より$BG=BD-GD=6-4=2$
$\triangle BCG$と$\triangle ECF$の相似比が$2:1$であることより、$EF = \frac{1}{2}BG=1$が分かる。
ウより、$DF=EF=1$である。
さらに、$h=k=i$より二角相等で$\triangle DEF \backsim \triangle DCG$が成り立つ。この相似比は $EF:CG=1:4$なので、$DE=\frac{1}{4}DC = \frac{1}{4}(DF+FC)=\frac{1}{4}(1+2)=\frac{3}{4}$
したがって、$GE=BD-DE=6-2-\frac{3}{4}=\frac{13}{4}$となり、求める長さは$\frac{13}{4}$ cm である。
志望校に合わせた受験対策なら、やる気アシストにお任せ下さい！
家庭教師のやる気アシストは、静岡県にお住まいの受験生のお子さんを毎年たくさん指導をさせ頂き、合格に導いています。
高い合格率の秘訣は、指導経験豊富な先生の指導力に加え、1対1の指導でお子さん一人ひとりの状況に合わせた、お子さんだけのカリキュラムで勉強が進められるから！
家庭教師のやる気アシストは、お子さんの志望校合格まで全力でサポートさせて頂きます！
LINE問合せ窓口
LINEからもお問合せいただけます！
公式Instagram
勉強のお役立ち情報を配信中！
お問い合わせ、ご質問も受付中です！
ご質問などお気軽にお問い合わせください。
アシストの指導方法がじっくり見れる！知れる！無料の体験授業実施中
お子さんにとって「成果が出る勉強法」ってどんな勉強法だと思いますか？
お子さんそれぞれに、個性や性格、学力の差もあります。そんな十人十色のお子さん全員に合う勉強法ってなかなかないんです。
たからこそ、受験生の今だけでもお子さんだけの勉強法で受験を乗り越えてみませんか？
やる気アシストには、決まったカリキュラムはありません。お子さんの希望や学力、得意や不得意に合わせて、お子さんだけのカリキュラムで指導を行っていきます。また、勉強法もお子さんそれぞれに合う合わないがあります。無料体験授業では、お子さんの性格や生活スタイルを見せていただき、お子さんにとって効率的な成果の出る勉強のやり方をご提案させて頂きます。
