







兵庫県の2024年3月実施の令和6年度(2023年度)入学者の公立高校入試問題の解説をしています。
受験勉強において、過去問を解くことはとても効果的な勉強法です。ぜひ、受験までに一度挑戦し、問題の傾向を掴んでおきましょう。合わせて、対策などをたてられるととても良いですね。
また、過去問で苦手な点が見つかった場合は、そこを中心に試験日当日までにしっかりと対策しておきましょう。
(1) 6 ÷(-2) を計算しなさい。
(2) 3(2x+y) -(x-4y) を計算しなさい。
(3) 3√5+√20 を計算しなさい。
(4) 2次方程式 x2+5x+3=0を解きなさい。
(5) yはxに反比例し、x=-6 のとき y=3である。 x =2 のときのyの値を求めなさい。
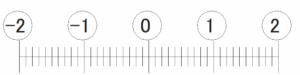
(6) 絶対値が2以下である整数すべての和を求めなさい。
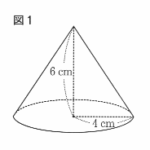
(7) 図1のように、底面の半径が4cm 、高さが6cm の円すいがある。この円すいの体積は 何 cm3か、 求めなさい。ただし、 円周率は πとする。
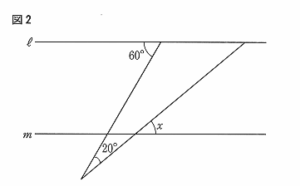
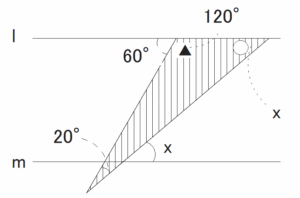
(8) 図2で、ℓ//m のとき、 ∠xの大きさは何度か、 求めなさい。
(1) 6÷(-2)= -3
(2) 3(2x+y)-(x-4y) = 6x+3y-x+4y = 5x+7y
(3) 3√5+√20 = 3√5+2√5 = 5√5
(4) x²+5x+3=0解の公式:ax²+bx+c=0の時、
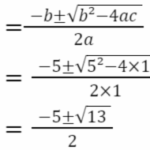
(5) y = a/xに、(x,y) = (-6,3)を代入すると、
3 =-a/6 となり a = -18
よってy = -18/x に x = 2 を代入して、答えは y = -9
(6) 0
絶対値が2以下の整数は下の図の通りで、合計は-2+-1+0+1+2=0
(7) 32π (㎤)
底面積は、π×4²
よって、体積は、16π×6×1/3=32π (㎤)
| 錐の体積の求め方 : 底面積×高さ×1/3 |
(8) 40°
右図の斜線部分の三角形に着目すると、▲は直線 l において、180°-60°=120°
また、直線 l // 直線 m より、〇 = x
よって、三角形の内角の和が180°であるのでx =180°- (120°+20°) = 40°
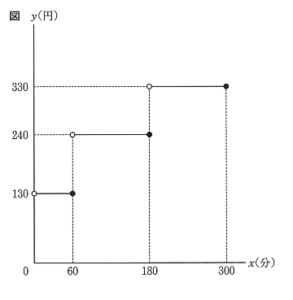
2つの駐輪場A, B があり、 表1は自転車1台を駐輪場Aに駐輪する場合の料金の設定の一部を、 表2は自転車1台を駐輪場Bに駐輪する場合の料金の設定を表したものである。図は自転車1台を駐輪場Aに駐輪する場合について、駐輪時間 x分と料金 y円の関係をグラフに表したものである。
ただし、駐輪時間は連続する時間とする。あとの問いに答えなさい。
表1
駐車場A
| 駐車時間 | 料金 |
| 60分まで | 130円 |
| 180分まで | 240円 |
| 300分まで | 330円 |
表2
駐車場B
基本料金を100円とする。
駐輪時間が20分を超えるごとに、20円ずつ基本料金に加算する。
例:駐輪時間をx分とすると、料金は、
0 < x ≦ 20 のとき 100円
20 < x ≦ 40 のとき 120円
40 < x ≦ 60 のとき 140円
(1) 自転車1台を駐輪場Aに100分駐輪するときの料金は何円か、 求めなさい。
(2) 自転車1台を駐輪場Bに駐輪する場合について、駐輪時間 x 分と料金 y 円の関係をグラフに表すと、
そのグラフ上に2点P (20,100), Q(40,120) がある。直線 PQ の式を求めなさい。
(3) 自転車1台を180分までの時間で駐輪する。このとき、駐輪場Aに駐輪する場合の料金と、駐輪場Bに駐輪する場合の料金が等しくなるのは
駐輪時間が何分のときか、適切なものを次のア〜エから1つ選んで、その符号を書きなさい。
ア 120分を超えて140分まで イ 140分を超えて160分まで
ウ 160分を超えて180分まで エ 料金が等しくなる時間はない
(4) 自転車1台を180分を超えて300分までの時間で駐輪する。このとき、 駐輪場Aに駐輪する場合の料金よりも、
駐輪場Bに駐輪する場合の料金のほうが安くなる駐輪時間は最大で何分か、求めなさい。
(1) 表1から、240円
(2) y=x+80
直線PQの傾きは、40-20/120-100 = 20/20 = 1
よって、xy=ax+b とすると a = 1
y=x+b に P (20,100) を代入すると、
100=20+b より、b = 80よって、求める式は y=x+80
(3) イ
駐輪場Bは基本料金が100円、その後の課金は20円のため駐車料金が130円になることはない
よって、240円になる場合を考える
(2)の式にy=240を代入すると、
240 = x +80 から、x =160
つまり140< x ≦160の場合で、答えはイ
(4) 240分
表1から、駐車場Aの駐車料金は330円なので、駐車場Bの駐車料金が330円よりも安くなる場合を考えると、
y = 320 の時、最大の x となる。
よって、320 = x + 80から、 x = 240
表1
駐車場A
| 駐車時間 | 料金 |
| 60分まで | 130円 |
| 180分まで | 240円 |
| 300分まで | 330円 |
次の問いに答えなさい。
(1) 数学の授業で、 先生がAさんたち生徒に次の[問題]を出した。
[問題]
2つの奇数の積は、偶数になるか、 奇数になるか考えなさい。
また、2つの偶数の積、 偶数と奇数の積についても考えなさい。
Aさんは、[問題]について、 次のように考えた。【 I 】にあてはまる1以外の自然数、 【 Ⅱ 】にあてはまる式をそれぞれ求めなさい。
また、【 Ⅲ 】、【 Ⅳ 】、【 Ⅴ 】にあてはまる語句の組み合わせとして適切なものを、あとのア〜クから1つ選んで、その符号を書きなさい。
まず、2つの奇数の積について考える。
m、n を整数とすると、 2つの奇数は2m+1 、2n+1 と表される。 この2つの奇数の積は、(2m+1) (2n+1) と表すことができ、変形すると、
(2m+1)(2n+1) =4mn + 2m+2n+1
=【 I 】 ( 【 Ⅱ 】 )+1
【 Ⅱ 】は整数だから、 【 I 】 ( 【 Ⅱ 】 )は【 Ⅲ 】である。
したがって、2つの奇数の積は【 Ⅳ 】である。
同じようにして考えると、 2つの偶数の積、 偶数と奇数の積はどちらも【 Ⅴ 】である。
| ア Ⅲ 偶数 Ⅳ 偶数 Ⅴ 偶数 イ Ⅲ 偶数 Ⅳ 偶数 Ⅴ 奇数 ウ Ⅲ 偶数 Ⅳ 奇数 Ⅴ 偶数 エ Ⅲ 偶数 Ⅳ 奇数 Ⅴ 奇数 オ Ⅲ 奇数 Ⅳ 偶数 Ⅴ 偶数 カ Ⅲ 奇数 Ⅳ 偶数 Ⅴ 奇数 キ Ⅲ 奇数 Ⅳ 奇数 Ⅴ 偶数 ク Ⅲ 奇数 Ⅳ 奇数 Ⅴ 奇数 | |
(2) 大小2つのさいころを同時に1回投げ、 大きいさいころの出た目の数を a 小さいさいころの出た目の数を b とする。
次の確率を求めなさい。 ただし、 さいころの1から6までのどの目が出ることも同様に確からしいとする。
① ab の値が奇数となる確率を求めなさい。
② ab + 3b の値が偶数となる確率を求めなさい。
③ a2-5ab +6b2の値が3以上の奇数となる確率を求めなさい。
(1) 【I】 2, 【Ⅱ】 2mn+m+n, 【Ⅲ,Ⅳ,Ⅴ】 ウ
(2m+1)(2n+1) = 4mn+2m+2n+1
= 2(2mn+m+n)+1
[2mn+m+n] は整数だから、
[2][(2mn+m+n)]は[偶数]である。
したがって、2つの奇数の積は奇数である。
同じようにして考えると…
2つの偶数はそれぞれ、2m、 2nと表される。
この2つの偶数の積は 2m×2n= 4mnで、mnは整数なので、4mnは偶数である。
また、偶数と奇数はそれぞれ2m、2n+1と表され、この2つの偶数と奇数の積は
2m×(2n+1) = 2{m(n+1)}
=2(mn+m)で、偶数となる。
よって、2つの偶数の積、2つの偶数と奇数の積はどちらも偶数となる。
(2) ① 1/4, ② 3/4, ③ 2/9
① (1)から、2つの整数の積が奇数となるのは、2つの奇数の積であるから、abが積となるのは、a,bどちらも奇数の場合である。
1つのサイコロで奇数が出る確率は、1/2 である
から、1/2×1/2 = 1/4
② ab+3b=b(a+3)と変形することができ、積が偶数となる場合はbが偶数、または(a+3)が偶数の場合である。
つまり、bが奇数かつ(a+3)が奇数の場合以外は全て偶数となる。
bが奇数となる確率は 1/2
(a+3)が奇数となる確率はa=2,4,6の場合の 1/2
よって、求める確率は、1-(1/2×1/2) = 3/4
③ a²-5ab+6b² を変形すると、
(a-3b)(a-2b) と表すことができるので、(a-3b),(a-2b)がそれぞれ奇数になる場合を考える。
この時、(a-2b)に着目すると、aが偶数の場合、2bが偶数なので、aは必ず奇数だと分かる。
さらに、aが奇数のとき(a-3b)に注目すると、bは偶数でないといけないと分かる。
つまり、a= 1,3,5、b= 2,4,6 の場合で考えると、
(a,b) = (1,2)の場合
(a-3b)(a-2b) = (1-3×2)(1-2×2) = 15
(a,b) = (1,4)の場合
(a-3b)(a-2b) = (1-3×4)(1-2×4) = 77
(a,b) = (1,6)の場合
(a-3b)(a-2b) = (1-3×6)(1-2×6) =187
(a,b) = (3,2)の場合
(a-3b)(a-2b) = (3-3×2)(3-2×2) = 3
(a,b) = (3,4)の場合
(a-3b)(a-2b) = (3-3×4)(3-2×4) = 45
(a,b) = (3,6)の場合
(a-3b)(a-2b) = (3-3×6)(3-2×6) = 135
(a,b) = (5,2)の場合
(a-3b)(a-2b) = (5-3×2)(5-2×2) = -1
(a,b) = (5,4)の場合
(a-3b)(a-2b) = (5-3×4)(5-2×4) = 21
(a,b) = (5,6)の場合
(a-3b)(a-2b) = (5-3×6)(5-2×6) = 91
よって、(a,b) = (5,2)の場合のみ不適となるため、
求める確率は 8/36 = 2/9
図のように、関数y=ax2 のグラフ上に2点A, B があり、 点Aの座標は (-2,1)、 点Bのx座標は4である。
またy軸上にy座標が1より大きい点Cをとる。 次の問いに答えなさい。
(1) a の値を求めなさい。
(2) 次の【 ア 】、【 イ 】にあてはまる数をそれぞれ求めなさい。
関数 y=ax2 について、 xの変域が -2 ≦ x ≦ 4 のとき、yの変域は、【 ア 】≦ y ≦ 【 イ 】 である。
(3) 直線ABの式を求めなさい。
(4) 線分AB、AC をとなり合う辺とする平行四辺形ABDCをつくると、
点Dは関数y=ax2のグラフ上の点となる。
① 点Dの座標を求めなさい。
② 直線y=2x+8上に点Eをとる。
△ABEの面積が平行四辺形ABDCの面積と等しくなるとき、
点Eの座標を求めなさい。
ただし、 点Eのx座標は正の数とする。
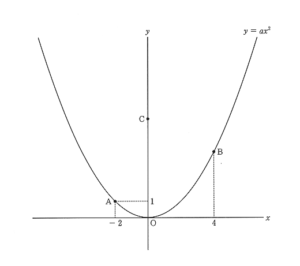
(1) a=1/4
点Aがy=ax²を通ることから、1=a×(-2)²
よって、a=1/4
(2) ア 0 イ 4
グラフから、x=0のときyは最小値 0となり、x=4のときに最大となる。
y= 1/4x² に x=4を代入すると、y=4
よって 0≦ y ≦4]
(3) y=x/2+2
直線ABは2つの点、A(-2,1) B(4,4) を通るから傾きは、
(4-1) / (4-(-2))= 3/6=1/2
y=1/2x+b に(-2,1)を代入すると、
1= 1/2 ×(-2)+bよってb=2となり、求める式は y= x/2+2
よってb=2となり、求める式は y= x/2+2
(4) ① D(6,9) ② 点E(4/3, 32/3)
① ABのx座標の差は6であるから点Cから点Dの差も6となり、点Dのx座標は6である。
点Dは、y=1/4x²上の点であるから、y= 1/4×6²=9 よって、D(6,9)
② 右の図のように、△ABEが平行四辺形ABDCの面積と等しくなる時は、△ABEが△ABCの2倍になるときである。
CDとAB共に平行である直線で、Cよりもy座標が4大きいつまり、(0,10)を通る直線を直線Lとすると、直線L // CD // ABより、傾きは1/2
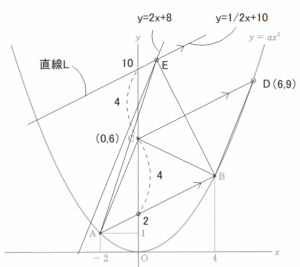
図1のように、 ∠ACB=90°、AB=4cm、 AC=3cmの直角三角形ABCがあり、
辺AB上にBD=1cmとなる点Dをとる。 2点A、Dを通り、 辺BC に点Eで接する円Oがある。
次の問いに答えなさい。
(1) 線分BE の長さを次のように求めた。 【 Ⅰ 】【 Ⅱ 】【 Ⅲ 】にあてはまる
最も適切なものを、あとのア~キからそれぞれ1つ選んで、その符号を書きなさい。
また、【 Ⅳ 】にあてはまる数を求めなさい。
図2のように,直線EOと円Oとの交点のうち、点Eと異なる点をFとし、
まず、△ABE∽△EBDであることを証明する。
△ABE と △EBD において、
共通な角だから、
∠ABE = ∠EBD ‥‥‥①
弧DEに対する円周角は等しいから、
∠DAE = ∠【 Ⅰ 】 ‥‥‥②
△DEF は、辺 EF を斜辺とする直角三角形であるから、
∠【 Ⅰ 】 + ∠DEF = 90° ‥‥‥③
また, OE ⊥ BC であるから、
∠DEF + ∠【 Ⅱ 】 = 90° ‥‥‥④
③、④より、
∠【 Ⅰ 】 = ∠【 Ⅱ 】 ‥‥‥⑤
②、⑤より、
∠BAE = ∠【 Ⅱ 】 ‥‥‥⑥
①、⑥より、2組の角がそれぞれ等しいから、
△ABE ∽ △EBD
したがって、AB : EB = 【 Ⅲ 】
このことから、 BE = 【 Ⅳ 】 cm
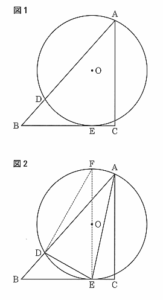
| ア ADE イ AEF ウ BED エ DFE オ BD : BE カ BE : BD キ BE : DE | |
(2) 線分 CE の長さは何cmか、 求めなさい。
(3) 円Oの半径の長さは何cmか、 求めなさい。
(1) 【I】 エ, 【Ⅱ】 ウ, 【Ⅲ】 カ, 【Ⅳ】 2
図のように、直線EOと円Oのうち、
点Eと異なる点をFとし、まず、
△ABEと△EBDにおいて共通な角だから
∠ABE=∠EBD ‥‥‥①
弧DEに対する円周角は等しいから、
∠DAE=∠DFE ‥‥‥②
△DEFは辺EFを斜辺とする直角三角形であるから、
∠DFE+∠DEF = 90° ‥‥‥③
また、OE⊥BCであるから
∠DEF+∠BED = 90° ‥‥‥④
③,④より、
∠DFE=∠BED = 90° ‥‥‥⑤
②,⑤より、
∠BAE=∠BED = 90° ‥‥‥⑥
①,⑥より、2組の角がそれぞれ等しいから
△ABE∽△EBD
したがって AB:EB = BE:BD
このことから、4:BE = BE:1
BE² = 4
よって、BE=2cm
(2) CE = √7-2
△ABCにおいて、三平方の定理を利用すると、
AB² = AC² + BC²
4² = 3² + BC² より BC=√7
(1) よりBE = 2であるから、EC = √7-2
(3) r= 10-2√7 / 3
図のように、点OからACに垂線を下した交点をHとすると、
OH = EC = √7-2
AH = AC-HC = AC-OE = 3 – r
△ABCにおいて、三平方の定理を利用すると
r²=(√7-2)²+(3-r)²
r²=7-6√7+4+9-6r+r²
よって、r= 10-2√7 / 3
ゆうきさん、りょうさん、まことさんの3人は、 兵庫県内のいくつかの市町における2022年1月
から2022年12月までの、月ごとの降水日数 (雨が降った日数)を調べた。
次の問いに答えなさい。ただし、1日の降水量が1mm以上であった日を雨が降った日、
1mm未満であった日を雨が降らなかった日とする。
(1) 表1は西宮市の月ごとの降水日数のデータである。
このデータの中央値 (メジアン)は何日か、 求めなさい。

(気象庁Webページより作成)
(2) 図は、豊岡市、三田市、洲本市について、それぞれの市の月ごとの降水日数のデータを、 ゆうきさんが箱ひげ図に表したものである。
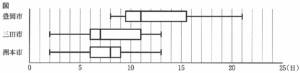
(気象庁Webページより作成)
① りょうさんは、図から次のように考えた。 りょうさんの考えの下線部a、bは、それぞれ図から読みとれることとして正しいといえるか、
最も適切なものを、あとのア〜ウからそれぞれ1つ選んで、その符号を書きなさい。
りょうさんの考え
a三田市の範囲と洲本市の範囲は等しいが、b平均値は三田市より洲本市のほうが大きい。
| ア 正しい イ 正しくない ウ 図からはわからない | |
② まことさんは、調べた市町について、それぞれの市町の月ごとの
降水日数のデータを度数分布表にまとめることにした。
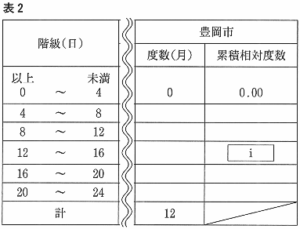
表2はその一部、豊岡市についての度数分布表である。
表2の【 i 】にあてはまる数を、図から読みとり求めなさい。
ただし、小数第2位までの小数で表すこと。
(3) 3人は降水確率について興味をもち、 さらに調べると「ブライアスコア」 という値について知った。
<ブライアスコア>
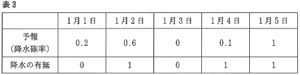
降水確率の精度を評価する値の1つであり、 表3のような表を用いて、 あとの(ⅰ)~(ⅳ)の手順で求める。
(ⅰ) それぞれの日の「予報 (降水確率)」の欄には、 降水確率を記入する。
(ⅱ) それぞれの日の「降水の有無」の欄には、実際にその日に雨が降った場合は1、 雨が降らなかった場合は0を記入する。
(ⅲ) それぞれの日について、(ⅰ)、(ⅱ)で記入した数の差の2乗の値を求める。
(ⅳ) (ⅲ) で求めた値のn日間分の平均値がn日間のブライアスコアとなる。
例1 : 表3の1月1日と1月2日の2日間のブライアスコアは、
{(0.2 −0)2+(0.6−1)2}÷2=0.1
例2 : 表3の5日間のブライアスコアは、
{(0.2 −0)2+(0.6−1)2+(0−0)2+(0.1−1)2+(1−1)2}÷5=0.202
ある年の2月1日から9日の降水について調べると、 表4のようであり、 2月7日から9日の「降水の有無」はわからなかった。
また、 2月1日から3日までの3日間のブライアスコアと、 2月4日から6日までの3日間のブライアスコアは等しかった。
ただし、 0 ≦ x<0.5 , 0 ≦ y ≦1 とする。

① y を x の式で表しなさい。
② 2月1日から9日の降水について、 さらに次のことがわかった。
• 2月7日から9日の3日のうち、 2日は雨が降り、 1日は雨が降らなかった。
• 2月7日から9日までの3日間のブライアスコは、2月1日から6日までの6日間のブライアスコアより、15分の2だけ小さかった。
このとき、xの値を求めなさい。 また、 2月7日から9日の3日のうち、 雨が降った日の組み合わせとして適切なものを、
次のア〜ウから1つ選んで、その符号を書きなさい。
ア 2月7日と8日 イ 2月7日と9日 ウ 2月8日と9日
(1) 7.5日
表1のデータを小さい順に並び変えると、
2,2,4,5,7,7,8,9,10,10,11,14
中央値(メジアン)は、データを半分に分ける値のことである。データの数が偶数の場合は真ん中の2つの数の平均が中央値となるため、
今回は7と8の平均の7.5が中央値となる。
(2) ① a ア, b ウ ② i=0.75
② 図から第3四分位数は15.5となる。
8日以上16未満の月は34であるので、 i=0.75
(3) ① y=-x+1 ② x=0.3 ウ
① 2月1日から3日までのブライアスコアは、
{(x-0)²+(y-0)²+(0.5-0)²}÷3
=(x²+y²+0.25) ÷3
=x²+y²+0.25 / 3
2月4日から6日までのブライアスコアは、
{(x-1)²+(y-1)²+(0.5-1)²}÷3
=(x²-2x+1+y²-2y+1+0.25) ÷3
=x²-2x+y²-2y+2.25 / 3
よって、これらが等しいことから、
x²+y²+0.25=x²-2x+y²-2y+2.25
2x+2y=2
y=-x+1 になる
② 2月1日から 6日までのブライアスコアを計算すると、
(x-0)²+(-x+1-0)²+(0.5-0)²+(x-1)²+(-x+1-1)²+(0.5-1)² / 6
=x²+x²-2x+1+0.25+x²-2x+1+x²+0.25 /6
=4x²-4x+2.5 / 6
=2x²-2x+1.25 / 3 ‥‥‥①
ア、イ、ウについてそれぞれについて2月7日から9日までのブライアスコアを考える
アの場合、2月7日から9日までのブライアスコアは
=(x-1)²+(-x+1-1)²+(0.5-0)² / 3
=(x²-2x+1+x²+0.25) / 3
=(2x²-2x+1.25) / 3
となり、これは①と同じとなってしまうためアは不適
イの場合、2月7日から9日までのブライアスコアは
(x-1)²+(-x+1-0)²+(0.5-1)²/3
=x²-2x+1+x²-2x+1+0.25/3
=2x²-4x+2.25/3
これが、①より2/15だけ小さい場合を考えると、
2x²-4x+2.25/3+2/15=2x²-2x+1.25/3 ←①
(2x²-4x+2.25)+ 25 =(2x²-4x+2.2/5)
2x= 7/5
よって x= 710
ただし、条件より0≦x<0.5なので、これは不適
ウの場合、2月7日から 9日までのブライアスコアは
(x-0)²+(-x+1-1)²+(0.5-1)²/3
=(x²+x²+0.25)/3
=(2x²+0.25)/3
これが、➀より215だけ小さい場合を考えると、
(2x²+0.25)/3+ 2/15 =2x²-2x+1.25/3 ←①
(2x²+0.25)+ 2/15 =(2x²-2x+1.25)
2x= 3/5
x=3/10 = 0.3
よってウが適切。
家庭教師のやる気アシストは、兵庫県にお住まいの受験生のお子さんを毎年たくさん指導をさせ頂き、合格に導いています。
高い合格率の秘訣は、指導経験豊富な先生の指導力に加え、1対1の指導でお子さん一人ひとりの状況に合わせた、お子さんだけのカリキュラムで勉強が進められるから!
家庭教師のやる気アシストは、お子さんの志望校合格まで全力でサポートさせて頂きます!
お子さんにとって「成果が出る勉強法」ってどんな勉強法だと思いますか?
お子さんそれぞれに、個性や性格、学力の差もあります。そんな十人十色のお子さん全員に合う勉強法ってなかなかないんです。
たからこそ、受験生の今だけでもお子さんだけの勉強法で受験を乗り越えてみませんか?
やる気アシストには、決まったカリキュラムはありません。お子さんの希望や学力、得意や不得意に合わせて、お子さんだけのカリキュラムで指導を行っていきます。また、勉強法もお子さんそれぞれに合う合わないがあります。無料体験授業では、お子さんの性格や生活スタイルを見せていただき、お子さんにとって効率的な成果の出る勉強のやり方をご提案させて頂きます。

