【新潟県】令和5年度/2023年度入学者高校入試選抜試験：数学の解説
新潟県の2023年3月実施の令和5年度（2023年度）入学者の公立高校入試問題の解説をしています。
受験勉強において、過去問を解くことはとても効果的な勉強法です。ぜひ、受験までに一度挑戦し、問題の傾向を掴んでおきましょう。合わせて、対策などをたてられるととても良いですね。
また、過去問で苦手な点が見つかった場合は、そこを中心に試験日当日までにしっかりと対策しておきましょう。
大問1 小問集合
問題文
次の（1）～（8）の問いに答えなさい。
（1）$7-(-3)-3$を計算しなさい。
（2）$2(3a-2b)-4(2a-3b)$を計算しなさい。
（3）$(-6ab)^2 \div 4ab^2$を計算しなさい。
（4）連立方程式$\begin{cases}x+3y=21\\2x-y=7\end{cases}$を解きなさい。
（5）$\sqrt{45}-\sqrt{5}+\frac{10}{\sqrt{5}}$を計算しなさい。
（6）130人の生徒が1人$a$円ずつ出して、1つ$b$円の花束を5つと、1本150円のボールペンを5本買って代金を払うと、お釣りがあった。このとき、数量の関係を不等式で表しなさい。
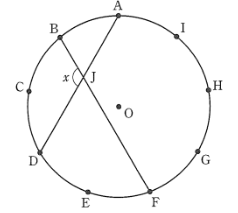
（7）次の図のように、円$O$の醜状に演習を9等分する9つの点A、B、C、D、E、F、G、H、Iがある。
線分ADと線分BFの交点をJとするとき、$\angle x$の大きさを求めなさい。
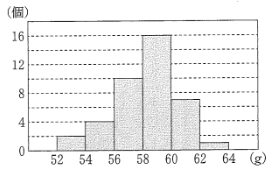
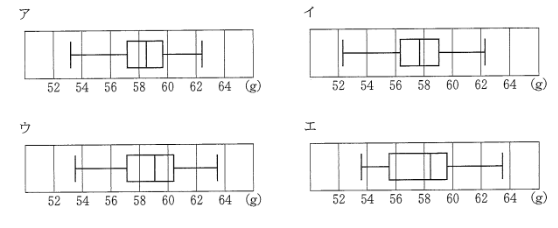
（8）次の図は、ある家庭で購入した卵40個の重さを1個ずつはかり、ヒストグラムに表したものである。このヒストグラムに対応する箱ひげ図として正しいものを、次のア～エから1つ選び、その符号を書きなさい。
ただし、階級は52g以上54g未満のように、2gごとの区間に区切っている。
解答・解説
（1）７
（2）$-2a+8b$
（3）$9a$
（4）$x=6$ $y=5$
（5）$4\sqrt{5}$
（6）$130a>5b+750$
（7）$120°$
$\angle ACB×2=∠AOB$ であることを利用
（8）ア
大問2 作図と確率
問題文
次の（1）～（3）の問いに答えなさい。
（1）1から6までの目のついた1つのさいころを2回投げるとき、1回目に出る目の数をa, 2回目に出る目の数をbとする。このとき、$\frac{24}{a+b}$が整数になる確率を求めなさい。
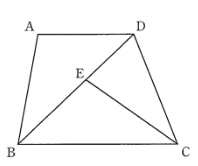
（2）次の図のように、$AD \ // \ BC$の台形ABCDがあり、$\angle BCD = \angle BDC$である。
$\angle DBA = \angle BCE$となる点Eをとるとき、$AB=EC$であることを証明しなさい。
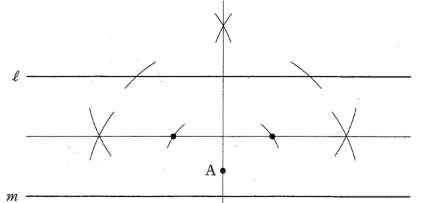
（3）下の図のように, 平行な2直線$l$、$m$と点Aがある。点Aを通り, 2直線$l$、$m$の両方に接する円の中心を、定規とコンパスを用いて、作図によってすべて求め、それらの点に$\bullet$をつけなさい。
ただし、作図は解答用紙に行い、作図に使った線は消さないで残しておくこと。
解答・解説
（1）$\frac{17}{36}$
次の表のように、さいころを2回投げたときの目の出方は全部で36通りある。
$\frac{24}{a+b}$が整数になる数、すなわち$24÷(a+b)$で割り切れる約数を見つければよい。
さいころの目の合計は$2 \le a + b \le 12$ であり、このうち、$a + b$ が24の約数となるのは、17通りある。
よって、$\frac{17}{36}$
| a\b | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
（2）解答例
$\triangle ABD$ と $\triangle ECB$ において、仮定より、 $\angle DBA = \angle BCE$ ･･･①
$\triangle BCD$ は $\angle BCD = \angle BDC$ の二等辺三角形であるから、$BD = CB$ ･･･②
$AD // BC$ より、$\angle ADB = \angle EBC$ ･･･③
①、②、③より、1辺とその両端の角がそれぞれ等しいから、$\triangle ABD \equiv \triangle ECB$
よって、$AB = EC$
等しい角を探し、二等辺三角形、錯覚の性質を用いることで三角形の合同条件を示そう。
（3）図を参照
0120-740-100
LINE問合せ窓口
LINEからもお問合せいただけます！
公式Instagram
勉強のお役立ち情報を配信中！
お問い合わせ、ご質問も受付中です！
ご質問などお気軽にお問い合わせください。
大問3 資料の活用
問題文
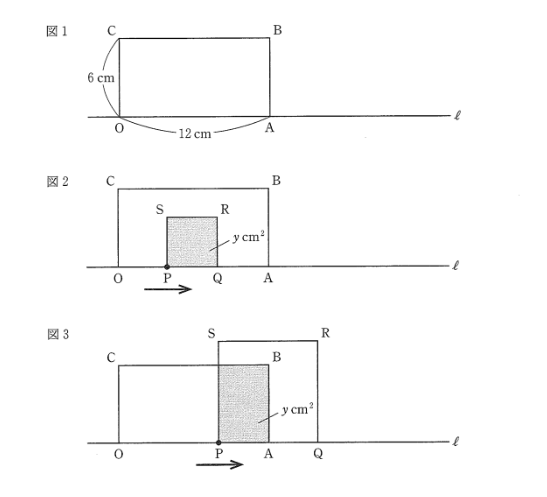
下の図1のように、$OA=12 \text{cm}$、$OC=6 \text{cm}$の長方形OABCがあり、2つの頂点O、Aは直線$l$上にある。点Pは、頂点Oを出発し、毎秒$2 \text{cm}$の速さで、図2、3のように直線$l$上を頂点Aまで移動する。また、線分OPの延長上に、OP=PQとなる点Qをとり、直線lについて長方形OABCと同じ側に、正方形PQRSをつくる。
点Pが頂点Oを出発してから、$x$秒後の長方形OABCと正方形PQRSの重なっている部分の面積を$y\text{cm}^2$とするとき、次の（1）～（4）の問いに答えなさい。ただし、点Pが頂点O、Aにあるときは、$y=0$とする。
（1）$x=2$のとき、$y$の値を答えなさい。
（2）次の①、②について、$x$を$y$の式で表しなさい。
$0 \leqq x \leqq 3$のとき
$3 \leqq x \leqq 6$のとき
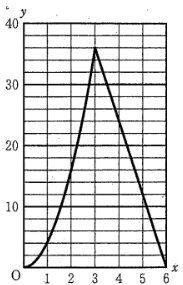
（3）$0 \leqq x \leqq 6$のとき、$x$と$y$の関係を表すグラフを書きなさい。
（④）$y=20$となる$x$の値を全て求めなさい。
解答・解説
（1）$y=16$
図を描いて計算すること。
（2）① $-y=4x^2$ ② $-y=-12x+72$
$x=3$ までは正方形 $PQRS$ は長方形 $OABC$ から出ることはない。しかし $x>3$ では正方形 $PQRS$ に長方形 $OABC$ と重ならない部分があることに注意。
（3）図を参照
（2）で求めた式のグラフを描く。
（4）$x = \sqrt{5}, \frac{13}{3}$
0 \le x \le 3$ のとき、$4x^2 = 20$ を解いて、$x = \pm \sqrt{5}$
$0 \le x \le 3$ から $x = \sqrt{5}$
$3 \le x \le 6$ のとき、$-12x + 72 = 20$ を解いて、$x = \frac{13}{3}$ これは、$3 \le x \le 6$ を満たす。
よって、$x = \sqrt{5}, \frac{13}{3}$
$y=20$を代入し、$x$を求める。なお、（3）で書いたグラフより、xが2つ存在することが分かる。
大問4 連立方程式
問題文
箱の中に、数字を書いた10枚のカード［1］［2］［3］［4］［5］［6］［7］［8］［9］が入っている。これらのカードを使い、次の手順Ⅰ～Ⅲに従って、記録用紙に数を記入していく。このとき、あとの（1）、（2）の問いに答えなさい。
手順
Ⅰ 箱の中から1枚のカードを取り出して、そのカードに書かれている数字を、記録用紙の1番目の欄に記入し。カードを箱の中に戻す。
Ⅱ 箱の中からもう一度1枚のカードを取り出して、そのカードに書かれている数字を、記録用紙の2番目の欄に記入し、カードを箱の中に戻す。
Ⅲ 次に、記録用紙の（$n-2$）番目の欄の数と（$n-1$）番目の欄の数の和を求め、その一の位の数を$n$番目の欄に記入する。ただし、$n$は3以上18以下の自然数とする。
記録用紙
| 1番目 | 2番目 | 3番目 | 4番目 | 5番目 | 6番目 | … | 16番目 | 17番目 | 18番目 |
（1）次の文は、手順Ⅰ～Ⅲに従って、記録用紙に数を記入するときの例について述べたものである。このとき、文中の【ア】～【ウ】に当てはまる数を、それぞれ答えなさい。
例えば、手順Ⅰで［2］のカード、手順Ⅱで［3］のカードを取り出したときには、下のように、記録用紙の1番目の欄には2、2番目の欄には3を記入する。このとき、16番目の欄に記入する数は【ア】、17番目の欄に記入する数は【イ】、18番目の欄に記入する数は【ウ】となる。
| 1番目 | 2番目 | 3番目 | 4番目 | 5番目 | 6番目 | … | 16番目 | 17番目 | 18番目 |
| 2 | 3 | 5 | 8 | 3 | 1 | … | 【ア】 | 【イ】 | 【ウ】 |
（2）手順Ⅰ、Ⅱで取り出したカードに書かれている数字と、手順Ⅲで記録用紙に記入する数に、どのような関係があるかを調べるために、次の表1、2を作った。
表1は、手順Ⅰで［0］〜［9］のいずれか1枚のカードを取り出し、手順Ⅱで［5］のカードを取り出したときのそれぞれの場合について、1番目の欄の数を小さい順に並べ替えてまとめたものである。また、表2は、手順Ⅰで［0］〜［9］のいずれか1枚のカードを取り出し、手順Ⅱで［6］のカードを取り出したときのそれぞれの場合について、1番目の欄の数を小さい順に並べ替えてまとめたものである。このとき、下の①、②の問いに答えなさい。
表1
| 1番目 | 2番目 | … | 16番目 | 17番目 | 18番目 |
| 0 | 5 | … | 0 | 5 | 5 |
| 1 | 5 | … | 7 | 5 | 2 |
| 2 | 5 | … | 4 | 5 | 9 |
| 3 | 5 | … | 1 | 5 | 6 |
| 4 | 5 | … | 8 | 5 | 3 |
| 5 | 5 | … | 5 | 5 | 0 |
| 6 | 5 | … | 2 | 5 | 7 |
| 7 | 5 | … | 9 | 5 | 4 |
| 8 | 5 | … | 6 | 5 | 1 |
| 9 | 5 | … | 3 | 5 | 8 |
表2
| 1番目 | 2番目 | … | 16番目 | 17番目 | 18番目 |
| 0 | 6 | … | 0 | 2 | 2 |
| 1 | 6 | … | 7 | 2 | 9 |
| 2 | 6 | … | 4 | 2 | 6 |
| 3 | 6 | … | 1 | 2 | 3 |
| 4 | 6 | … | 8 | 2 | 0 |
| 5 | 6 | … | 5 | 2 | 7 |
| 6 | 6 | … | 2 | 2 | 4 |
| 7 | 6 | … | 9 | 2 | 1 |
| 8 | 6 | … | 6 | 2 | 8 |
| 9 | 6 | … | 3 | 2 | 5 |
① 手順Ⅱで［5］、［6］以外のカードを取り出しても、17番目の欄の数は、1番目の欄の数に関係なく、2番目の欄の数によって決まる。このことを証明しなさい。
② 手順Ⅰで［$x$］のカード、手順Ⅱで［4］のカードを取り出したとき、18番目の欄の数が1になった。このとき。$x$の値を求めなさい。
解答・解説
（1）【ア】4 【イ】1 【ウ】5
16、17、18番目は手動で求める。式で求めるか、手計算で求めるかはnにより判断する。
（2）
①1番目の棚の数をa、2番目の棚の数をbとし、10の倍数を取り除きながら 17 番目まで順に書き出すと、a, b, a + b, a + 2b, 2a + 3b, 3a + 5b, 5a + 8b, 8a + 3b, 3a + b, a + 4b, 4a + 5b, 5a + 9b, 9a + 4b, 4a + 3b, 3a + 7b, 7a, 7b (17番目)
したがって、17 番目の棚の数は、1番目の棚の数に関係なく、2 番目の棚の数によって決まる。
1番目の数をa、2番目の数をbと置いて、10の倍数になったときに取り除く。この工程を経てn=17まで計算すれば、n=17のとき7bとなることが判明する。この数はaによらないことがわかる。
②1番目の数をa、2番目の数をbと置いて、10の倍数になったときに取り除く。この工程を経てn=17まで計算すれば、n=17のとき7bとなることが判明する。この数はaによらないことがわかる。 ①の際にn=16で7aとなることが判明している。7bは今回8であるため、n=18で7a+8となる。これが1となるためには、7a+8の下二桁が1であればよい。これを満たすaは、9のみである。
①の際にn=16で7aとなることが判明している。7bは今回8であるため、n=18で7a+8となる。これが1となるためには、7a+8の下二桁が1であればよい。これを満たすaは、9のみである。
LINE問合せ窓口
LINEからもお問合せいただけます！
公式Instagram
勉強のお役立ち情報を配信中！
お問い合わせ、ご質問も受付中です！
ご質問などお気軽にお問い合わせください。
大問5 空間図形
問題文
〔5〕下の図のような立体 $ABC – DEF$ があり、四角形 $ABED$ は、$BA = 5 \text{ cm}$、$BE = 10 \text{ cm}$ の長方形であり、$\triangle ABC$ と $\triangle DEF$ は正三角形である。
また、辺 $BE$ と辺 $CF$ は平行であり、$CF = 5 \text{ cm}$ である。
点 $C$ から辺 $BE$ に引いた垂線と辺 $BE$ との交点を $P$ とするとき、次の(1)～(3)の問いに答えなさい。
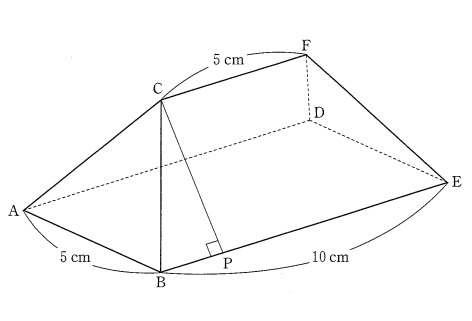
(1) 線分 $CP$ の長さを答えなさい。
(2) 5点 $C, A, B, E, D$ を結んでできる四角すいの体積を求めなさい。
(3) 4点 $A, B, C, F$ を結んでできる三角すいの体積を求めなさい。
解答・解説
（1）$\frac{5\sqrt{3}}{2}$
$BC=EF$ であるため、$BP=(10-5)/2=\frac{5}{2}$ とわかる。ピタゴラスの定理より $CP$ が計算できる。
（2）$\frac{125\sqrt{2}}{3}$
$C$ から長方形 $ABED$ へ垂線を落とす。その交点を $M$ とすれば、$PM=AB/2=\frac{5}{2}$ とわかる。これにピタゴラスの定理を用いれば $CM$ が導出できる長方形 $ABED$ の面積 $=50$ より、四角錐の体積が計算できる。
（3）$\frac{125\sqrt{2}}{12}$
辺 $AB$ の中点を $N$ とすると、求める三角錐の体積は、
$\frac{1}{3} \times (\triangle CFN \text{の面積}) \times AB = \frac{1}{3} \times \frac{1}{2} \times CF \times CM \times 5$
となる。
志望校に合わせた受験対策なら、やる気アシストにお任せ下さい！
家庭教師のやる気アシストは、新潟県にお住まいの受験生のお子さんを毎年たくさん指導をさせ頂き、合格に導いています。
高い合格率の秘訣は、指導経験豊富な先生の指導力に加え、1対1の指導でお子さん一人ひとりの状況に合わせた、お子さんだけのカリキュラムで勉強が進められるから！
家庭教師のやる気アシストは、お子さんの志望校合格まで全力でサポートさせて頂きます！
LINE問合せ窓口
LINEからもお問合せいただけます！
公式Instagram
勉強のお役立ち情報を配信中！
お問い合わせ、ご質問も受付中です！
ご質問などお気軽にお問い合わせください。
アシストの指導方法がじっくり見れる！知れる！無料の体験授業実施中
お子さんにとって「成果が出る勉強法」ってどんな勉強法だと思いますか？
お子さんそれぞれに、個性や性格、学力の差もあります。そんな十人十色のお子さん全員に合う勉強法ってなかなかないんです。
たからこそ、受験生の今だけでもお子さんだけの勉強法で受験を乗り越えてみませんか？
やる気アシストには、決まったカリキュラムはありません。お子さんの希望や学力、得意や不得意に合わせて、お子さんだけのカリキュラムで指導を行っていきます。また、勉強法もお子さんそれぞれに合う合わないがあります。無料体験授業では、お子さんの性格や生活スタイルを見せていただき、お子さんにとって効率的な成果の出る勉強のやり方をご提案させて頂きます。
