大阪府の2024年3月実施の令和6年度（2024年度）入学者の公立高校入試問題の解説をしています。
受験勉強において、過去問を解くことはとても効果的な勉強法です。ぜひ、受験までに一度挑戦し、問題の傾向を掴んでおきましょう。合わせて、対策などをたてられるととても良いですね。
また、過去問で苦手な点が見つかった場合は、そこを中心に試験日当日までにしっかりと対策しておきましょう。

大阪府の数学問題は、レベル別にＡＢＣの問題が用意されています。受験する学校によりどの問題を採用するかが異なります。
難易度は、Ａが易、Ｂがやや難、Ｃが難となっています。レベル差が顕著なので、各問題に対応する対策をとる必要があります。

 大阪府の公立高校入試情報はこちら

【数学A】大問1

問題文

次の計算をしなさい。

(1) 6 − (−1) × 2

(2) 9 ÷ (−3/4)

(3) 5² + (−15)

(4) x − 3 + 4(x + 1)

(5) 2xy × 3x

(6) 6√2 − √8

解答・解説

(1) 6-(-1)×2=6-(-2)=6+2=8

(2) 9÷(-3/4)=9×(-4/3)=-12

(3) 5²+(-15)=25-15=10

(4) x-3+4(x+1)=x-3+4x+4=5x+1

(5) 2xy ×3x=6x²y

(6) 6√2-√8=6√2-2√2=4√2

大問2

問題文

(1) a = 6 のとき、 3a – 5 の値を求めなさい。

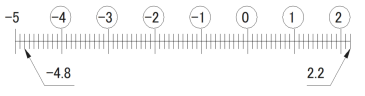
(2) -4.8 より大きく 2.2より小さい整数の個数を求めなさい。

(3) 次のア～エの式のうち、 「重さ a kgの荷物1個と重さ b kgの荷物1個の重さの合計は5kgより重い。」という数量の関係を正しく表しているものはどれですか。 一つ選び、記号を○で囲みなさい。
ア ab > 5　 イ a + b > 5　 ウ a + b < 5　 エ a + b = 5

(4) 連立方程式 5x + 2y = 11、 x + 2y = 15 を解きなさい。

(5) 二つのさいころを同時に投げるとき、 出る目の数の積が6である確率はいくらですか。 1から6までのどの目が出ることも同様に確からしいものとして答えなさい。

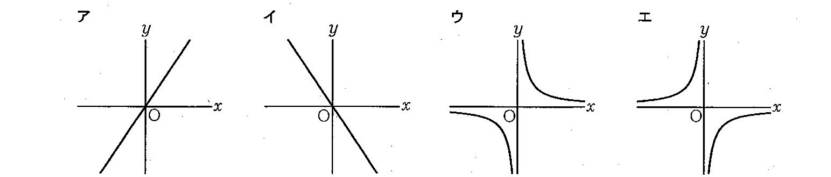
(6) a を正の定数とする。 次のア～エのうち、関数 y = a/x のグラフの一例が示されているものはどれですか。 一つ選び、記号を○で囲みなさい。

(7) 二次方程式 x² − 9 + 14 = 0 を解きなさい。

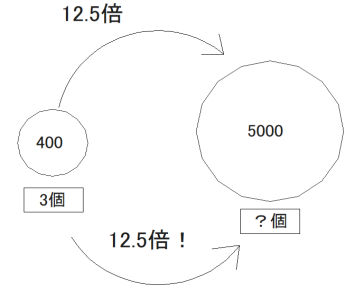
(8) ある工場で生産された 「製品 A」 がたくさんある。 それらのうちから400個を無作為に抽出して検査したところ3個の不良品が含まれていた。 標本調査の考え方を用いると、 この工場で生産された 「製品 A」 5000個の中に含まれる不良品の個数はおよそ何個と推定できますか。 答えは小数第1位を四捨五入して整数で書くこと。

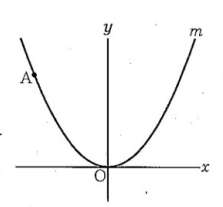
(9) 右の図において、 m は関数 y = ax² (aは定数)のグラフを表す。A は m 上の点であり、その座標は (-4 , 5)である。 a の値を求めなさい。

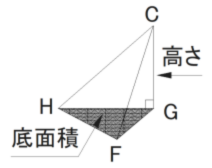
(10) 右の図において、 立体 ABCD – EFGH は直方体であり、 AB = 6cm、 AD = 5cm、 AE = 7cmである。 CとF、CとH、FとHとをそれぞれ結ぶ。

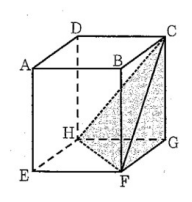
① 次のア～エのうち、 辺AB と平行な辺はどれですか。 一つ選び、 記号を○で囲みなさい。
ア 辺 AD　 イ 辺 BF　 ウ 辺 FG　 エ 辺 HG
② 立体 CGHF の体積を求めなさい。

解答・解説

(1) 3a – 5 に a = 6 を代入すると、3×6 – 5 = 18 – 5 = 13

(2) 7個

(3) イ
a と b の合計なので、a + b
これが5よりも大きいので、答えはイの a + b > 5

a > b ： a は b よりも大きい
a < b ： a は b よりも小さい
a ≧ b：a は b 以上
a ≦ b：a は b 以下

ということを覚えておこう！

(4) (x , y) = ( -1 , 8 )
①の式から②の式を引くと、

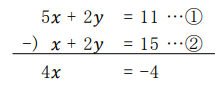
となり、x = -1 ということが分かる。
これを①に代入すると、
5×(-1) + 2y = 11
-5 + 2y = 11
2y = 11 + 5 = 16
よって、y = 8

(5) 1/9
2つのさいころを投げて出る目の数の積（掛け算の答え）が6となる組合せは (1,6), (2,3), (3,2), (6,1) の4通りある。
さいころの目の出方は全部で 6×6 = 36 通り
よって答えは 4/36 = 1/9

(6) ウ
a を正の定数、例えば 2 とすると、(x, y) = (1,2), (2,1), (-1,-2) となり、下記のグラフを描く

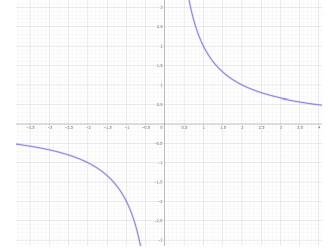
(7) x = 2 , 7
x² – 9x + 14 = 0
(x + a)(x + b) = 0 という形になることをイメージして、a×b = 14 , a+b = -9 になる数字を探す。
積が14になる整数の組合せは (a, b) = (1,14), (2,7), (-1,-14), (-2,-7)
このうち和が -9 になるものは (-2,-7)
よって、x² – 9x + 14 = 0 は (x – 2)(x – 7) = 0 と変形でき、答えは x = 2 , 7 になる。

(8) 38個
比を使って考えると、
400 : 5000 = 3 : x
400x = 15000
よって x = 37.5 → 四捨五入して 38 個

(9) a = 5/16
y = ax² に (x, y) = (-4 , 5) を代入すると、
5 = a × (-4 × -4) = a × 16
整理すると、a = 5/16

(10) ① エ　② 35㎤
三角錐の体積は「底面積 × 高さ × 1/3」で求められる。立体 CGHF の体積は、△HFG の面積 × CG の長さ × 1/3
= (6×5×1/2) × 7 × 1/3= 15 × 7 × 1/3 = 35

大問3

問題文

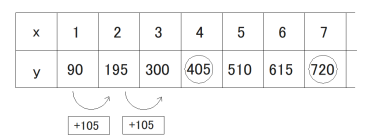
Uさんの学校の文化祭では、各クラスの企画を紹介する垂れ幕を作って体育館に飾ることになった。生徒会の委員であるUさんは、垂れ幕の枚数と垂れ幕の列の長さとの関係について考えてみた。下の図は、1枚の幅が90cm の垂れ幕を15cm間隔で飾ったときのようすを表す模式図である。「垂れ幕の枚数」が x 枚のときの「垂れ幕の列の長さ」を y cm とする。
x = 1 のとき y = 90 であるとし、x の値が1増えるごとに y の値は 105 ずつ増えるものとする。
次の問いに答えなさい。

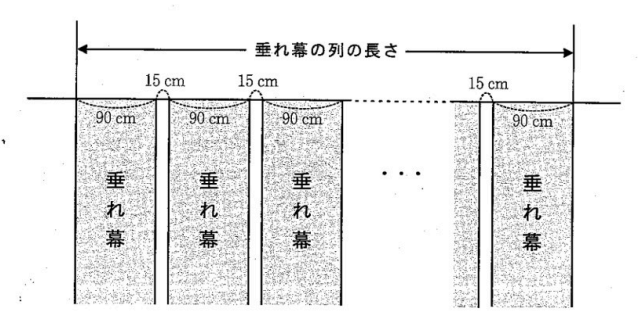
(1) 次の表は、x と y との関係を示した表の一部である。表中の (ア)、(イ) に当てはまる数をそれぞれ書きなさい。

(2) x を自然数として、y を x の式で表しなさい。

(3) y = 2085 となるときの x の値を求めなさい。

解答・解説

(1) (ア) 405　(イ) 720

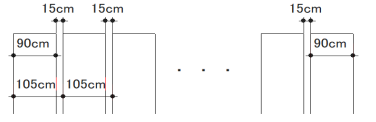
垂れ幕と隙間を合計すると105cmとなり、垂れ幕が1枚増えると105cmずつ増えることが分かる。
これを表であらわすと、

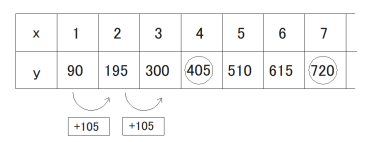
(ア) = 405、(イ) = 720 となる。

(2) y = 105x – 15
上記の表から、x = 2 以上の場合はひとつ前の y に +105 すればいいと分かる。
x = 1 のとき、y = 90 であるから、y = 90 + 105(x – 1) = 90 + 105x – 105 = 105x – 15

(3) x = 20
(2) で求めた式に y = 2085 を代入すると、
2085 = 105x – 15
2100 = 105x よって、x = 20

大問4

問題文

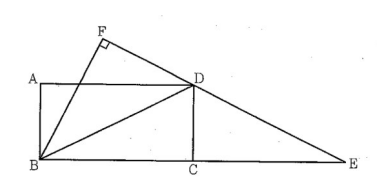
図において、四角形 ABCD は長方形であり、AB < AD である。△DBE は DB = DE の二等辺三角形であり、E は直線 BC 上にある。このとき、BC = CE である。F は、B から直線 DE にひいた垂線と直線 DE との交点である。

次の問いに答えなさい。

(1) 次のア～エのうち、四角形 ABCD を直線 BC を軸として1回転させてできる立体の名称として正しいものはどれですか。一つ選び、記号を○で囲みなさい。
ア 四角柱　 イ 四角すい　 ウ 円柱　 エ 円すい

(2) △FBD の内角 ∠FBD の大きさを a° とするとき、△FBD の内角 ∠BDF の大きさを a を用いて表しなさい。

(3) 次は、△FBE ∽ △ABD であることの証明である。【a】、【b】に入れるのに適している「角を表す文字」をそれぞれ書きなさい。また、c [ ] から適しているものを一つ選び、記号を○で囲みなさい。

(証 明)
△FBE と △ABD において

BF ⊥ FE だから ∠BFE = 90° …………………… [あ]
四角形 ABCD は長方形だから ∠【a】 = 90° …………………… [い]
[あ]、[い]より ∠BFE = ∠【a】 …………………… [う]
△DBE は DB = DE の二等辺三角形だから ∠FEB = ∠DBE …………………… [え]
AD ∥ BE であり、平行線の錯角は等しいから ∠【b】 = ∠DBE …………………… [お]
[え]、[お] より ∠FEB = ∠【b】 …………………… [か]
[う]、[か] より、c [ ア 1組の辺とその両端の角　 イ 2組の辺の比とその間の角　 ウ 2組の角 ]
がそれぞれ等しいから△FBE ∽ △ABD

(4) AB = 3cm、AD = 6cm であるときの線分 FB の長さを求めなさい。答えを求める過程がわかるように、途中の式を含めた求め方も説明すること。

解答・解説

(1) ウ

(2) 90 – a
三角形の内角の和は180°なので、∠BDF の大きさは 180 – 90 – a = 90 – a

(3) (a) BAD　(b) ADB　(c) ウ
△ABD に着目すると、
∠ABD = 180° – ∠BAD – ∠ADB
= 180° – 90° – ∠ADB
= 90° – ∠ADB

△FBE に着目すると、
∠FBE = 180° – ∠BFE – ∠FEB
= 180° – 90° – ∠FEB
= 90° – ∠FEB

∠ADB = ∠FEB なので、∠ABD = ∠FBE となる。

(4) 12√5 / 5
(3) より、△ABD ∽ △FBE なので、BD : BE = AB : FB

△ABD において三平方の定理を利用する。
BD² = AB² + AD²
BD² = 3² + 6² = 45
よって BD = 3√5

したがって、3√5 : 12 = 3 : FB

FB = 12√5 / 5

【数学B】大問1

問題文

(1) (−1)² − 2 × 3

(2) 3(x − 9y) + 4(x + 7y)

(3) 2b × 6a² ÷ (−4a)

(4) (x + 3)(x − 3) − x(x − 2)

(5) (√7 + 2√2)²

解答・解説

(1)
(-1)² – 2×3
= 1 – (2×3)
= 1 – 6
= -5

(2)
3(x – 9y) + 4(x + 7y)
= 3x – 27y + 4x + 28y
= 7x + y

(3)
2b × 6a² ÷ (-4a)
= 2b × 6a² × (-1 / 4a)
= -3ab

(4)
(x + 3)(x – 3) – x(x – 2)
= x² – 9 – (x² – 2x)
= x² – 9 – x² + 2x
= 2x – 9
※ (x + a)(x – a) = x² – a² を覚えておこう！

(5)
(√7 + 2√2)²
= (√7)² + 2×√7×2√2 + (2√2)²
= 7 + 4√14 + 4×2
= 7 + 4√14 + 8
= 15 + 4√14

大問2

問題文

(1) a = -3、b = 4 のとき、8a + b² の値を求めなさい。

(2) a を負の数とし、b を正の数とする。次のア～エの式のうち、その値がつねに正になるものはどれですか。一つ選び、記号を○で囲みなさい。
ア ab　 イ a + b　 ウ -a + b　 エ a – b

(3) 二次方程式 x² – 7x + 5 = 0 を解きなさい。

(4) n を自然数とする。√44n の値が自然数となる最も小さい n の値を求めなさい。

(5) 2から6までの自然数が書いてある5枚のカード [2]、[3]、[4]、[5]、[6] が箱に入っている。この箱から2枚のカードを同時に取り出し、取り出した2枚のカードに書いてある数の和を a、積を b とするとき、b – a の値が偶数である確率はいくらですか。どのカードが取り出されることも同様に確からしいものとして答えなさい。

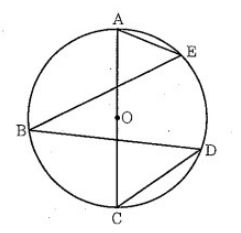
(6) 右の図において、A、B、C、D、E は円Oの周上の異なる5点であり、この順に左回りに並んでいる。線分AC は円Oの直径である。A と E、B と E、B と D、C と D とをそれぞれ結ぶ。鋭角 ∠AEB の大きさを a° とするとき、鋭角 ∠BDC の大きさを a を用いて表しなさい。

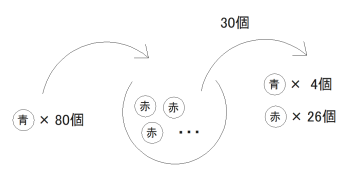
(7) 袋の中に赤色のビー玉だけがたくさん入っている。この袋に青色のビー玉を80個加えてよくかき混ぜた後、30個のビー玉を無作為に抽出したところ、4個が青色のビー玉であった。標本調査の考え方を用いると、袋の中には初めおよそ何個の赤色のビー玉が入っていたと推定できますか。

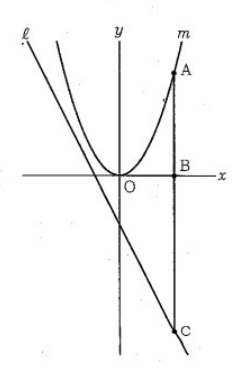
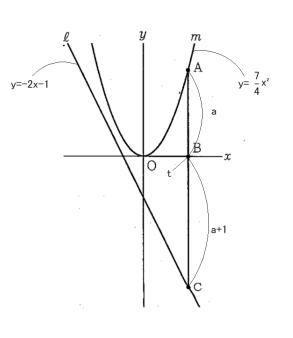
(8) 右の図において、m は関数 y = 7/4x² のグラフを表し、l は関数 y = -2x – 1 のグラフを表す。A は m 上の点であり、その x 座標は正である。A の x 座標を t とし、t > 0 とする。B は、A を通り y 軸に平行な直線と x 軸との交点である。C は、直線 AB と l との交点である。
線分 BC の長さが線分 AB の長さより 1cm 長いときの t の値を求めなさい。
答えを求める過程がわかるように、途中の式を含めた求め方も説明すること。
ただし、原点 O から点 (1,0) までの距離、原点 O から点 (0,1) までの距離はそれぞれ 1cm であるとする。

解答・解説

(1) -8
8a + b² に a = -3, b = 4 を代入すると、
8 × (-3) + 4²
= -24 + 16
= -8

(2) ウ
ア : (-) × (+) = (-) 常に負
イ : (-) + (+) a の絶対値が b よりも大きい場合は答えが負
ウ : -(-) + (+) = (+) + (+) 常に正
エ : (-) – (+) = (-) + (-) 常に負

(3) (7 ± √29) / 2
解の公式を利用する。
解の公式：ax² + bx + c = 0 の時、
x = -b ± √(b² – 4ac) / 2a
解の公式に当てはめると、
x = -(-7) ± √((-7)² – 4 × 1 × 5) / 2 × 1
x = 7 ± √29 / 2

(4) 11
√44 = √(4 × 11)
= 2 × √11
= 2√11
よって自然数となる最小の値は n = 11

(5) 3 / 10
取り出したカードのうち、1枚目の数を x、2枚目の数を y とすると、
a = x + y, b = xy, b – a = xy – (x + y)
と表すことができる。
差(引き算の答え)が偶数になるのは、偶数 – 偶数、奇数 – 奇数の場合。

ここで xy に着目すると、カードは 2, 3, 4, 5, 6 であり、xy が奇数となる組合せは 3,5 を取り出した場合のみである。
ただ、この場合は x + y が 8 で偶数となるため、差が奇数となる。

その他の組み合わせはすべて xy が偶数となるため、差が偶数になるカードの組合せを考えると、2 と 4、2 と 6、4 と 6 の場合 x + y が偶数になる。

よって b – a が偶数となる組合せは、(x, y) = (2,4), (4,2), (2,6), (6,2), (4,6), (6,4) の 6 通り。
カードの取り出し方は全部で 5 × 4 = 20 通りであるから、求める確率は 6 / 20 = 3 / 10

(6) 90° – a
右のように BC と CE に補助線を引くと、円周角の定理から、∠BDC = ∠BEC
また、∠AEC = 90° であるから求める角の大きさは 90° – a

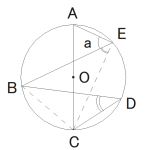
円周角の定理

(7) 520 個
下の図から袋の中の赤色の玉を x とおくと、
80 : x = 4 : 26
4x = 80 × 26 よって、520 個

(8) t = 8 / 7
点 A は m 上の点であるから、A(t, 7/4 t²)
点 C は l 上の点であるから、C(t, -2t – 1)
BC の長さが AB よりも 1 cm 長いことから
-(-2t – 1) – 7/4 t² = 1
2t + 1 – 7/4 t² = 1
7/4 t² – 2t = 0
t² – 8/7 t = 0
t(t – 8/7) = 0
t は 0 よりも大きいので、t = 8/7

大問3

問題文

Uさんの学校の文化祭では、各クラスの企画を紹介する垂れ幕を作って体育館に飾ることになった。生徒会の委員であるUさんは、垂れ幕の枚数と垂れ幕の列の長さとの関係について考えてみた。下の図は、同じ幅の垂れ幕を等間隔で飾ったときのようすを表す模式図である。垂れ幕1枚の幅はすべて 90 cm であり、垂れ幕どうしの間隔はすべて a cm である。「垂れ幕の枚数」が x 枚のときの「垂れ幕の列の長さ」を y cm とする。x = 1 のとき y = 90 であるとし、x の値が 1 増えるごとに y の値は (a + 90) ずつ増えるものとする。次の問いに答えなさい。

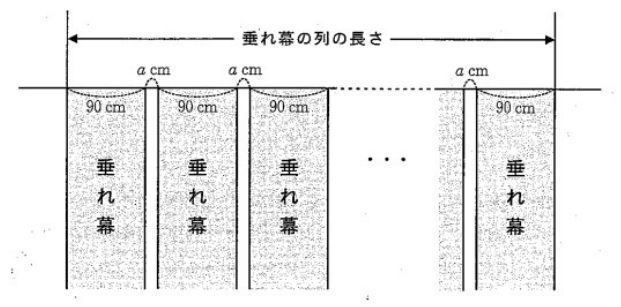
(1) Uさんは、a = 15 である場合について考えた。
① 次の表は、x と y との関係を示した表の一部である。表中の (ア)、(イ) に当てはまる数をそれぞれ書きなさい。

② x を自然数として、y を x の式で表しなさい。

③ y = 2085 となるときの x の値を求めなさい。

(2) Uさんは、21 枚の垂れ幕を等間隔で飾ったときに、垂れ幕の列の長さが 2130 cm になるようにしようと考えた。x = 21 のとき y = 2130 となる a の値を求めなさい。

解答・解説

(1)
① (ア) 405 (イ) 720

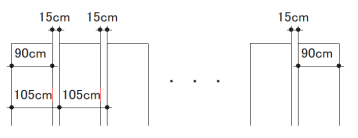
垂れ幕と隙間を合計すると105cmとなり、垂れ幕が1枚増えると105cmずつ増えることが分かる。これを表であらわすと、

となるため、(ア)405 (イ)720

② y = 105x – 15
上記の表から、x = 2 以上の場合はひとつ前の y に +105 すればいいと分かる。
x = 1 のとき、y = 90 であるから
y = 90 + 105(x – 1) = 90 + 105x – 105 = 105x – 15

③ a = 20
(2) で求めた式に y = 2085 を代入すると、
2085 = 105x – 15
2100 = 105x よって、x = 20

(2) a = 12
垂れ幕1枚の長さは 90 cm なので、21 枚の垂れ幕の長さは 21 × 90 = 1890 cm
図から垂れ幕のすき間は垂れ幕の数よりも1少ないので、隙間は 20 個ある。
以上から、
2130 = 1890 + 20a よって、a = 12

大問4

問題文

[ I ]
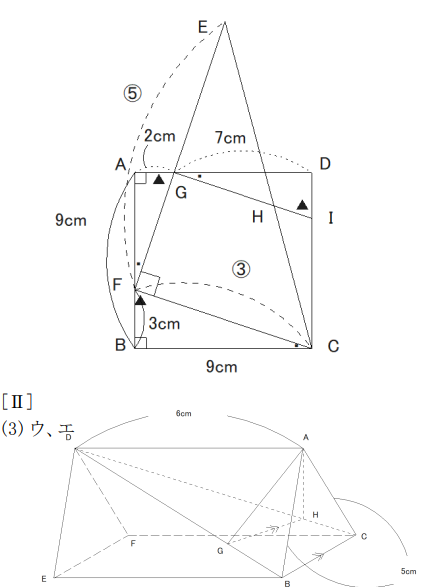
図 I において、四角形ABCDは1辺の長さが9cmの正方形である。△EFCは∠EFC=90°の直角三角形であり、EF > FC である。 Fは辺AB上にあってA、Bと異なる。 Gは、辺EF と辺 ADとの交点である。辺ECは、辺ADと交わっている。 Hは、Gを通り辺FCに平行な直線と辺ECとの交点である。Iは、 直線GHと辺DCとの交点である。

次の問いに答えなさい

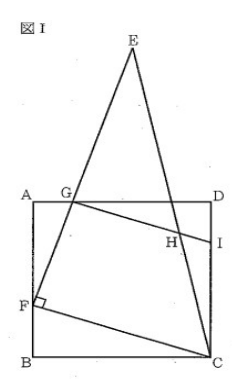
(1) △GAF∽△FBC であることを証明しなさい。

(2) FB = 3cm、 EF : FC = 5 : 3であるとき、
① 線分GFの長さを求めなさい。
② 線分HIの長さを求めなさい。

[Ⅱ]
図 II において、立体ABC – DEF は三角柱である。△ABC は、 AB = AC =5cmの二等辺三角形である。△DEF=△ABCである。四角形 DEBA、 FEBC、 DFCA は長方形であり、 AD=6cmである。 DとB、 DとCとをそれぞれ結ぶ。 G は、 線分 DB 上の点である。 Hは、Gを通り辺BC に平行な直線と線分DCとの交点である。AとG、AとHとをそれぞれ結ぶ。
次の問いに答えなさい。

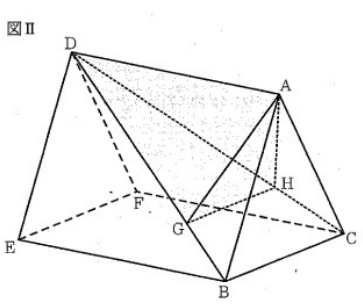
(3)次のア～オのうち、辺AB とねじれの位置にある辺はどれですか。 すべて選び、記号を○で囲みなさい。
ア 辺 AD イ 辺 DE ウ 辺 EF エ 辺 CF オ 辺 AC

(4) BC = 4 cm、GH = 3cmであるとき、
① △ABCの面積を求めなさい。
② 立体 ADGHの体積を求めなさい。

解答・解説

[Ⅰ]
(1) 四角形ABCDは正方形であるから、
∠GAF=∠FBC=90°⋯ア
∠AFG=180°-90°-∠CFB⋯①
△FBCの内角の和は180°であるから
∠BCF=180°-90°-∠CFB⋯②
よって、①②より
∠AFG= ∠BCF⋯イ
ア・イより、2組の角がそれぞれ等しいので
△GAF∽△FBC

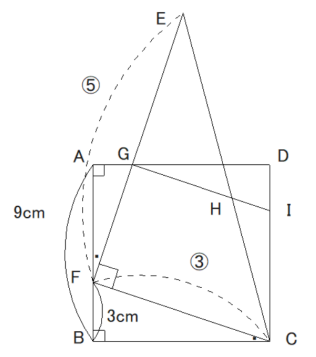
(2) ①GF=2√10 ②HI= 8√10/ 15
① AB=9cm FB=3cm よりAF=6cm
(1)より△GAF∽△FBCであり、相似比は AF：BC= 6：9 =2：3よって、AG=2/3×FB=2
△GAFにおいて、
三平方の定理を利用すると、GF²=AG²+AF² GF²=2²+6²=40 よってGF=2√10

② GI // FCであるから、∠FGI=90°よって∠DGI=180°-90°-∠AGF
また、四角形ABCDは正方形であるから∠GDI=90°
このことから△GAF∽△IDG AG=2,GD=AD-AG=9-2=7
また、相似比はAF:DG=6:7
①よりGF=2√10であるから、GI=7/6×2√10⋯(a)
GI // FC、∠FEC=∠GEHであることから、
△EGH∽△EFC
CF=3/2 GF=3/2×2√10＝3√10
また、条件より、CF：EF=3：5 EF=5√10なので、
EG=EF-GF=5√10-2√10=3√10
よって、三角形と比の定理より、
EF：EG=5√10：3√10＝5：3
GH=3/5×5√10：3√10＝5：3
GH=3/5×3√10＝9√10 / 5 ⋯(b)
よって、(a),(b)より、HI = 8√10 / 15

(4) ① 2√21 ② 9√21 / 4
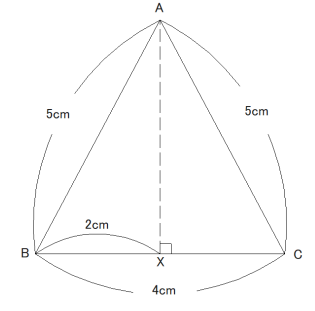
①△ABCにおいて、点AからBCに向けて下した垂線の交点をXとすると、△ABCが二等辺三角形であることから
BX=CX=2cm
また、△ABXにおいて三平方の定理を利用すると、
AB²＝BX²+AX²
これより、AX=√21
よって、求める面積は、4×√21×1/2＝2√21

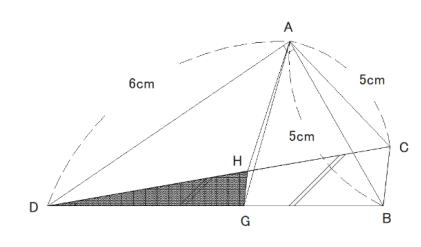
② GH // BC より、△DGH∽△DBC また、相似比は、GH：BC =3：4
立体ADGHと立体ADBCにおいて、底面をそれぞれ△DGH、△DBCとすると、高さは等しいので、体積比は、底面積の比と同じになる。
よって、それぞれの体積をV、V’とすると
V：V’= 3²：4² = 9：16

また、立体DABCは三角柱のため、その体積は
△ABCの面積×高さ(AD)×1/3
=2√21×6×1/3
=4√21

よって、V+V’=8√21、V：V’= 9：16

 大阪府のその他の過去問を見る

志望校に合わせた受験対策なら、やる気アシストにお任せ下さい！

家庭教師のやる気アシストは、大阪府にお住まいの受験生のお子さんを毎年たくさん指導をさせ頂き、合格に導いています。

高い合格率の秘訣は、指導経験豊富な先生の指導力に加え、1対1の指導でお子さん一人ひとりの状況に合わせた、お子さんだけのカリキュラムで勉強が進められるから！
家庭教師のやる気アシストは、お子さんの志望校合格まで全力でサポートさせて頂きます！

 アシストの受験対策をもっとみる

アシストの指導方法がじっくり見れる！知れる！無料の体験授業実施中

お子さんにとって「成果が出る勉強法」ってどんな勉強法だと思いますか？
お子さんそれぞれに、個性や性格、学力の差もあります。そんな十人十色のお子さん全員に合う勉強法ってなかなかないんです。
たからこそ、受験生の今だけでもお子さんだけの勉強法で受験を乗り越えてみませんか？

やる気アシストには、決まったカリキュラムはありません。お子さんの希望や学力、得意や不得意に合わせて、お子さんだけのカリキュラムで指導を行っていきます。また、勉強法もお子さんそれぞれに合う合わないがあります。無料体験授業では、お子さんの性格や生活スタイルを見せていただき、お子さんにとって効率的な成果の出る勉強のやり方をご提案させて頂きます。