







兵庫県の2025年3月実施の令和7年度(2025年度)入学者の公立高校入試問題の解説をしています。
受験勉強において、過去問を解くことはとても効果的な勉強法です。ぜひ、受験までに一度挑戦し、問題の傾向を掴んでおきましょう。合わせて、対策などをたてられるととても良いですね。
また、過去問で苦手な点が見つかった場合は、そこを中心に試験日当日までにしっかりと対策しておきましょう。
ア およそ100個
イ およそ120個
ウ およそ140個
エ およそ160個
$4\sqrt{2}-3\sqrt{2}=\sqrt{2}$
$(x-a)^2=x^2-2ax+a^2$の公式を使います。
$(1,4)(2,2)(4,1)(-1,-4)(-2,-2)(-4,-1)$の6つがあります。
球の体積は$\frac{4πr^3}{3}$で求めます。
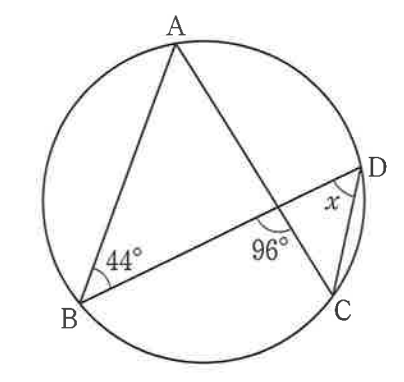
円周角の性質と三角形の外角の性質を用います。
$\frac{6}{20}\times400$で求まります。
次の規則にしたがい, 1番目の数と2番目の数を定めて, 3番目から8番目までの数を順に求める。 あとの問いに答えなさい。
[規則]
・1番目の数と2番目の数を、自然数から自由に定める。
・3番目以降の数は,その2つ前の数と1つ前の数の和とする。
例えば,1番目の数が1,2番目の数が2のとき,数を順に求めると,表のようになる。

① 大きいさいころの出た目の数を α, 小さいさいころの出た目の数を6として, 6番目の数を a, bを 用いて表しなさい。
② 3番目の数が 11 になる確率を求めなさい。
③ 1番目から3番目までの3つの数の和が10の倍数になる確率を求めなさい。
④ 8番目の数から7番目の数をひいた値が5の倍数にならない確率を求めなさい。
| 1番目 | 2番目 | 3番目 | 4番目 | 5番目 | 6番目 |
| 2 | 1 | 3 | 4 | 7 | 11 |
| 1番目 | 2番目 | 3番目 | 4番目 | 5番目 | 6番目 |
| a | b | a+b | a+2b | 2a+3b | 3a+5b |
$a+b=11$となるときなので、$(5,6)(6,5)$の2通りです。
よって、$\frac{2}{36}=\frac{1}{18}$
$a+b+(a+b)=2(a+b)$から、$(a+b)$が5の倍数か10の倍数であらば、$2(a+b)$が10の倍数になるので、
$(1,4)(2,3)(3,2)(4,1)(4,6)(5,5)(6,4)$の7通りです。
よって、$\frac{7}{36}$
8番目から7番目を引いた数は、6番目の数となります。
※下記参照
| 1番目 | 2番目 | 3番目 | 4番目 | 5番目 | 6番目 | 7番目 | 8番目 |
| a | b | a+b | a+2b | 2a+3b | 3a+5b | 5a+8b | 8a+13b |
$(8a+13b)-(5a+8b)=3a+5b$
5の倍数にならない確率は、bが何であっても5の倍数になることから、3aが5の倍数にならなければよいので、$a=1,2,3,4,6$です。
よって、$5\times6=30$通りあり、$\frac{30}{36}=\frac{5}{6}$
図1のように,関数y=ax²のグラフ上に2点A,Bがあり,点Aの座標は(-1, 1), 点Bのx座標はbである。 関 数y=ax²について, xの変域が-1≦x≦bのとき,yの変域が0≦y≦4である。また,点Bを通り,傾きが3/4の直線と, y 軸との交点をCとする。
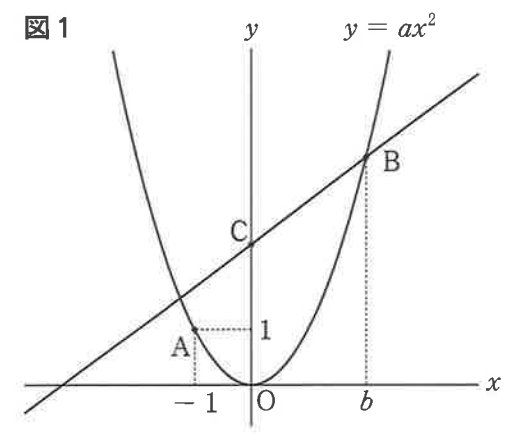
次の問いに答えなさい。 ただし, 座標軸の単位の長さは1cmとする。
$y=ax^2$に点$A(-1,1)$を代入します。
$1=a\times(-1)^2$
$y=ax^2$の変域を考えたときに、x=bのときに、y=4となることが分かるので
$b^2=4$
$b=\pm2$
yの変域の最小値が0なので、原点をxの変域が挟まないといけません。
つまり、$b>0$だから、$b=2$
2点$A(-1,1),B(2,4)$を通るので、連立方程式を解くと$a=1,b=2$となります。
つまり、直線ABの式は$y=x+2$です。
まず点Cの座標を求めます。
点$B(2,4)$を通り、傾きが$\frac{3}{4}$なので、
$4=2\times\frac{3}{4}+b$
$b=\frac{5}{2}$
よって、直線BCの式は$y=\frac{3}{4}x+\frac{5}{2}$
点$C(0,\frac{5}{2})$
さらに、直線ABの切片は2なので、△ABCの底辺は$\frac{5}{2}-2=\frac{1}{2}$となります。
高さは$1+2=3$なので、△ABCの面積は$\frac{1}{2}\times3\div2=\frac{3}{4}cm^2$となります。
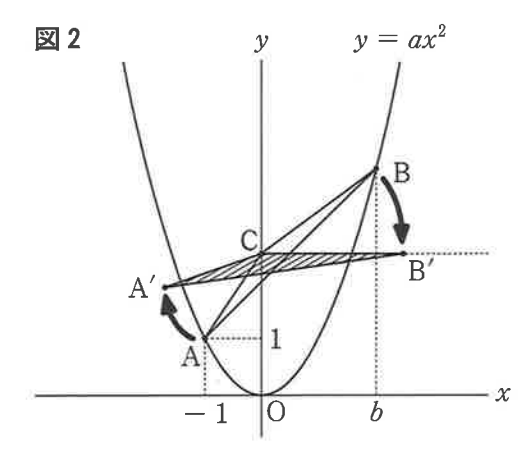
平行移動前後でBCの長さは変わらないことに注目すると
BCの長さは移動前の三平方の定理より$\sqrt{(2)^2+(4-\frac{5}{2})^2}=\sqrt{\frac{25}{4}}=\frac{5}{2}$
つまり、移動後の点B’の座標は$(\frac{5}{2},\frac{5}{2})$だと分かります。
ここで、△A’B’Cに注目すると、底辺がBC、高さがCのy座標からA’のy座標を引いた値だと分かります。
そして、移動前後で三角形の面積は変わらないので
$\frac{5}{2}\times(\frac{5}{2}-y(A’のy座標))\div2=\frac{3}{4}$
$y=\frac{10}{19}$
100 個の玉と1つの空の箱があり, 次のようにして, Aさん, Bさん, Cさん, Dさんの4人に玉を分ける。
[作業1]
・玉をAさんに18個, Bさんに 14 個渡す。 Cさんに渡す玉の個数は, Bさんに渡す玉の個数より少なく,Cさんに渡す個数の3倍の個数の玉をDさんに渡す。
[作業 2]
・空の箱に,[作業1] で残った玉を入れる。
[作業 3]
• 箱から玉を4個取り出し, 4人に1個ずつ渡す。
まず,[作業1], [作業2] を行い,その後, [作業3] を何回か繰り返して行っていくと, 箱の中の玉が ちょうど0個になり, 100個の玉を4人に分けることができた。 ただし, [作業3] を始めてから玉を箱に戻すことはない。次の問いに答えなさい。
[作業1]でCさんに玉をx個渡したとすると,[作業1]で4人に渡した玉の合計はx を用いて, [i]個と表すことができる。
また,[作業 3]をy回行ったときに, 箱の中の玉がちょうど0個になったとすると,[作業 2]で箱 に入れた玉はyを用いて,[ii]個と表すことができる。
玉は全部で100個なので, [i]+[ii]=100
等式の性質を使ってこの等式を変形すると,
箱の中の玉がちょうど0個になったとき,[iii]は [iv]個だとわかる。
ア AさんとDさんが持っている玉の合計
イ BさんとCさんが持っている玉の合計
ウ Aさんが持っている玉
エ Cさんが持っている玉
Dさんには$3x$個渡すことになるので
$18+14+x+3x=4x+32$
1回につき4個取り出すので、$4\times y=4y$
$4x+32+4y=100$
$4x+4y=68$
$x+y=17$
ちょうど0になったとは$y=0$なので、
$x=17$となります。
Aに注目するとB,C,Dで合わせて$17+54=71$個あるので、Aは29個になっている。
このことから元々持っていた18個から11個増えていることが分かります。
つまり、Bは$14+11=25$個なので、Dの個数は$54-25=29$個だと分かります。
図1のように,∠ABC が鋭角, AB=3cm, 辺BCを底辺としたときの高さが5cmの平行四辺形ABCD があり, ∠ABE=∠CBE, ∠BCF=∠DCFとなるように,辺AD上に2点E,Fをとると,線分BEと線分CFは点Gで交わり,EF=1cmとなった。
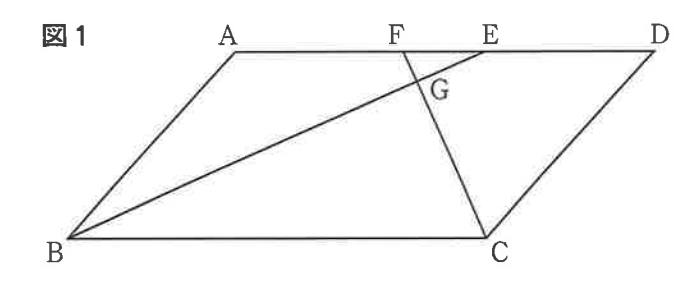
次の問いに答えなさい。
<証明>
△BCG と △EFG において,
[i]は等しいから, ∠BGC = ∠EGF …①
平行線の錯角は等しいので, AD // BC から,∠CBG = ∠[ii] …②
①,②より,2組の角がそれぞれ等しいから, △BCG ∽ △EFG
ア 中心角
イ 同位角
ウ 対頂角
エ EFG
オ FEG
カ GED
△ABEは二等辺三角形だと分かるので
$3-1=2$cmです。
△ECFに注目します。
錯角より∠DFC=∠DCF、平行四辺形の対角の大きさは等しいので、∠FDC=∠ABE×2
すると、∠DFC+∠ABE=90°だと分かるので、△FGEに注目すると、∠FGE=90°だとわかります。
BからADの延長線上に垂線を引いて、交点をHとします。
すると、△ABHで三平方の定理を用いてHA=2cm
△BHEで三平方を用いて、BE=$\sqrt{30}$cm
△BHE∽△FGEより
$BH:BE=FG:FE$
$\sqrt{5}:\sqrt{30}=FG:1$
$FG=1\times\sqrt{5}\div\sqrt{30}=\frac{\sqrt{6}}{6}$cm
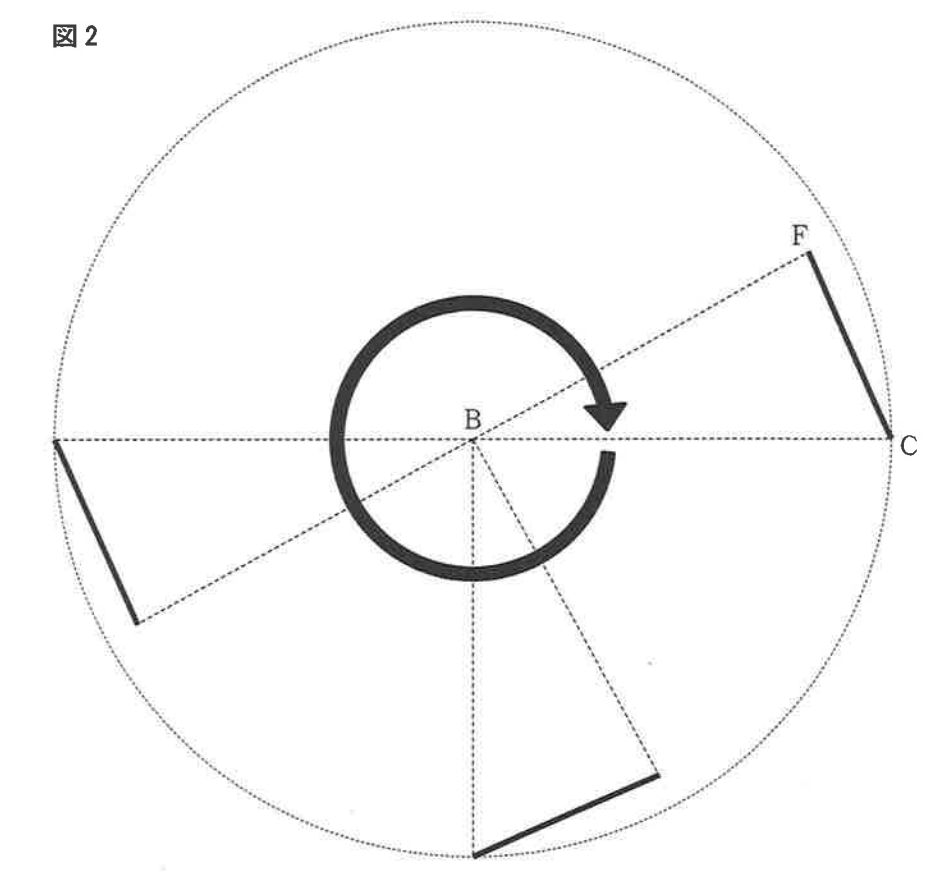
中心から一番遠い点を半径とする円の面積から、中心から一番近い点を半径とする円の面積を引くと答えになります。
一番遠い点はC、一番近い点はGになります。
$BC=AD=5cm$
$BG=5\times\frac{5}{\sqrt{30}}=\frac{5\sqrt{30}}{6}cm$
よって、$5^2π-(\frac{5\sqrt{30}}{6})^2π=\frac{25}{6}πcm^2$
花粉の飛散数の測定方法の1つに[ダーラム法]という方法がある。 あとの問いに答えなさい。
[ダーラム法]
花粉の飛散数の測定方法の1つであり, 次の(I)〜(V)の手順で求める。
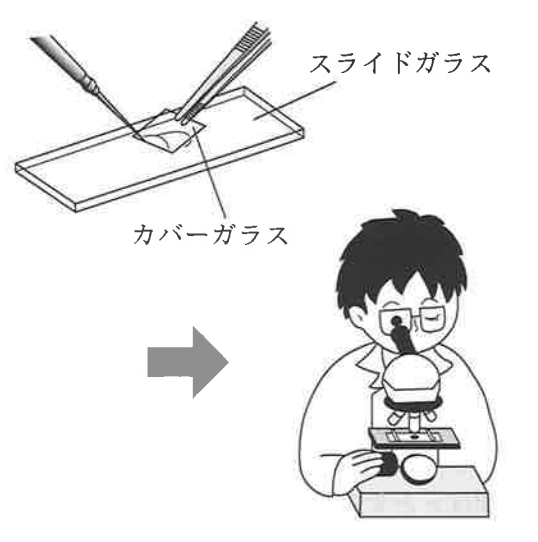
(I) 花粉が付着しやすいようにワセリンを塗ったスライドガラスを屋外に1日置いて,花粉を採取する。
(II) 回収したスライドガラス上の花粉を染色する。
(III) スライドガラスに,面積が3.24cm²のカバーガラスをかけ, プレパラートをつくる。
(IV) プレパラートを顕微鏡で観察し, カバーガラスの下にある花粉の数を数える。
(V) (IV)の値から, 1cmあたりの花粉の数を小数第1位まで求め,これを花粉の飛散数とし, 単 位は,個/cm²とする。 ただし, 小数第1位までで割り切れない場合は, 小数第2位を四捨五入する。
求めた花粉の飛散数をもとに, ランクに分ける。
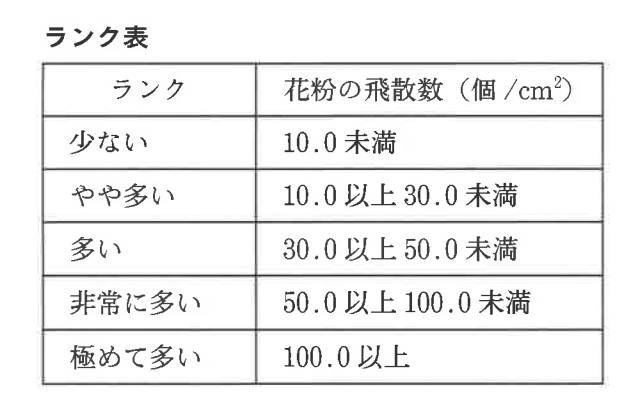
例えば, 3.24cm²のカバーガラスの下に, 162個の花粉があった場合, 花粉の飛散数は50.0個/cm²,ランクは「非常に多い」である。
ア 少ない
イ やや多い
ウ 多い
エ 非常に多い
オ 極めて多い
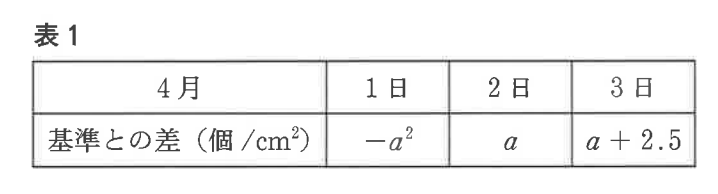
ア 表1のαが-4以上4以下の整数ならば、4月1日のランクは 「多い」である。
イ 表1のαが-4以上4以下の整数ならば、4月2日の飛散数は4月3日の飛散数より少ない。
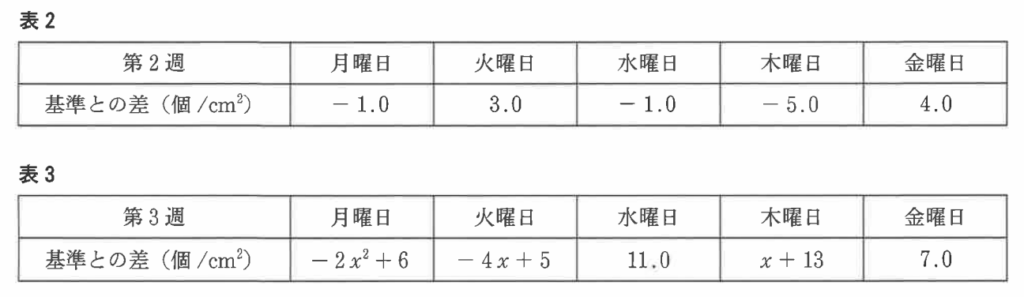
① 表2の5日間の飛散数の平均値は何個/cm2 か, 求めなさい。
② 表2と表3を合わせた10日の飛散数の平均値はちょうど34.0個/cm²であった。 また, 表3の5日のランクはすべて「多い」であり,表3の5日の中で,飛散数が同じである日の組み合わせはなかった。 表3のxの値を求めなさい。
また, はるかさんは平均値を求めた過程を振り返り、平均値を効率的に求める方法について,次のように考察した。[i],[ii]にあてはまる数をそれぞれ求めなさい。
【平均値の求め方】
・第3週の5日のランクはすべて「多い」であったから、基準を 40.0 個/cm²として,平均値を 求めることもできる。 基準を40.0個/cm²として,表3と同様にして第3週について新たな表を作成すると,「基準との差」の5つの数の中で最大の値は[i]で、 「基準との差」の5 つの数の和は[ii]である。
・[ii]の絶対値と,表3の「基準との差」の5つの数の和の絶対値を比較すると,[ii]の絶対値の方が小さいので, 第3週の平均値を求めるときは,基準を 40.0個/cm²として求める方が効率的だと考える。
$81\div3.24=25$個/cm²なので、やや多いになります。
$-1.0+3.0-1.0-5.0+4.0=0$となるので基準値の30個/cm²となります。
基準値を40個/cm²に設定することによって表3の各項目は-10されます。
これらの和が-10になるので
$(-2x^2-4)+(-4x-5)+(1)+(x+3)+(-3)=-10$
$2x^2+3x-2=0$
$x=-2,\frac{1}{2}$
$x=-2$の時は基準の30を下回ってしまうので、$x=0.5$
よって、最大の値は3.5、5つの数の和は-10.0になります。
家庭教師のやる気アシストは、兵庫県にお住まいの受験生のお子さんを毎年たくさん指導をさせ頂き、合格に導いています。
高い合格率の秘訣は、指導経験豊富な先生の指導力に加え、1対1の指導でお子さん一人ひとりの状況に合わせた、お子さんだけのカリキュラムで勉強が進められるから!
家庭教師のやる気アシストは、お子さんの志望校合格まで全力でサポートさせて頂きます!
お子さんにとって「成果が出る勉強法」ってどんな勉強法だと思いますか?
お子さんそれぞれに、個性や性格、学力の差もあります。そんな十人十色のお子さん全員に合う勉強法ってなかなかないんです。
たからこそ、受験生の今だけでもお子さんだけの勉強法で受験を乗り越えてみませんか?
やる気アシストには、決まったカリキュラムはありません。お子さんの希望や学力、得意や不得意に合わせて、お子さんだけのカリキュラムで指導を行っていきます。また、勉強法もお子さんそれぞれに合う合わないがあります。無料体験授業では、お子さんの性格や生活スタイルを見せていただき、お子さんにとって効率的な成果の出る勉強のやり方をご提案させて頂きます。

