







神奈川県の2025年3月実施の令和7年度(2025年度)入学者の公立高校入試問題の解説をしています。
受験勉強において、過去問を解くことはとても効果的な勉強法です。ぜひ、受験までに一度挑戦し、問題の傾向を掴んでおきましょう。合わせて、対策などをたてられるととても良いですね。
また、過去問で苦手な点が見つかった場合は、そこを中心に試験日当日までにしっかりと対策しておきましょう。
次の計算をした結果として正しいものを,それぞれあとの1~4の中から 1 つずつ選び,その番号を 答えなさい。
(ア) -4+(-11)
1:-15
2:-7
3:7
4:15
(イ)1/6-4/7
1:-31/42
2:-17/42
3:17/42
4:31/42
(ウ)36a²b²×6b÷8a
1:27ab²
2:27ab3
3:48ab²
4:48ab3
(エ)2x+y/3 – x-3y/5
1:7x-14y/15
2:7x-4y/15
3:7x+4y/15
4:7x+14y/15
(オ)(4+√3)(4-√3)-2(1-√3)
1:5+2√3
2:11+4√3
3:11+2√3
4:11+4√3
(ア)1
(与式)=$-4-11=-15$
(イ)2
(与式)=$\frac{7}{42}-\frac{24}{42}=-\frac{17}{42}$
(ウ)2
分数の形にして通分すると計算がしやすいです。
(与式)=$\frac{36a^2b^2\times6b}{8a}=-27ab^3$
(エ)4
(与式)=$\frac{5(2x+y)-3(x-3y)}{15}=\frac{7x+14y}{15}$
(オ)3
(与式)=$16-3-2+2\sqrt{3}=11+2\sqrt{3}$
次の問いに対する答えとして正しいものを,それぞれあとの 1 ~ 4 の中から 1 つずつ選び,その番号 を答えなさい。
(ア)(x-5)²-7(x-5)-18を因数分解しなさい。
1:(x-14)(x-7)
2:(x-14)(x-3)
3:(x-7)(x-4)
4:(x-4)(x-3)
(イ) 2 次方程式 5x²+7x+1=0 を解きなさい。
1:x=-7±√29/10
2:x=-7±√69/10
3:x=7±√29/10
4:x=7±√69/10
(ウ)関数 y=-4x²について,x の値が-5 から-1 まで増加するときの変化の割合を求めなさい。
1:-24
2:-16
3:16
4:24
(エ)ある工場で生産している製品 A について,今週と先週に生産した個数を比べると,今週は先週より 1 割増え,今週と先週に生産した個数をあわせると 567 個だった。
このとき,この工場で今週に生産した製品 A の個数を求めなさい。
1:270個
2:283個
3:284個
4:297個
(オ)4 < √n < 5 をみたす自然数 n のうち, √2n が整数となるような n の値を求めなさい。
1:n=12
2:n=18
3:n=24
4:n=32
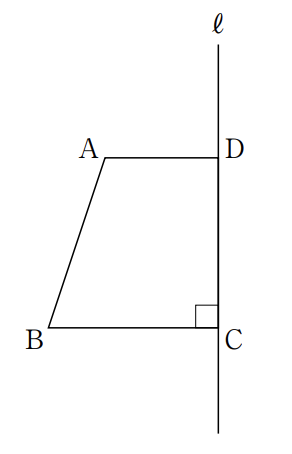
(カ)図において,四角形ABCDは AD//BC,∠BCD=90°の台形であり, 2 点 C,D は直線ℓ上の点である。
AD=2 cm,BC=CD=3 cm のとき,この台形を,直線ℓを軸として 1 回転させてできる立体の体積を求めなさい。ただし,円周率はπとする。
1:13πcm³
2:15πcm³
3:19πcm³
4:25πcm³
(ア)2
$(x-5)$をXとして因数分解をすると良いです。
(与式)=$X^2-7X-18=(X-9)(X+2)=(x-5-9)(x-5+2)=(x-14)(x-3)$
(イ)1
解の公式を用いて解けばよいです。
(与式)=$\frac{-7\pm\sqrt{49-20}}{10}=\frac{-7\pm\sqrt{29}}{10}$
(ウ)4
変化の割合は$\frac{yの増加量}{xの増加量}$で求めることができるので、
$\frac{-100-(-4)}{-5-(-1)}=\frac{-96}{-4}=24$
(エ)4
先週生産した個数をx個とすると
$x+1.1x=567$という式が成り立つので
$x=270$です。
今週は先週の1.1倍になったので、$1.1\times270=297$
(オ)2
$4^2<(\sqrt{n})^2<5^2$
$16<n<25$
よって、$n=17,18,19,20,21,22,23,24$
$2n=34,36,38,40,42,44,46,48$
このうち、$\sqrt{2n}$が整数となるのは$2n=36$となる$n=18$が答えとなります。
(カ)3
回転体は円すい台になります。
円すいの頂点をOとすると、相似比は△OAD:△OBC=2:3なので
$OD=DC\times2=6cm$
体積比は相似比の3乗なので8:27となり、円すい台は$27-8=19$の比だと分かります。
よって、$3\times3\timesπ\times9/div3\times\frac{19}{27}=19πcm^3$
次の問いに答えなさい。
(ア)右の図 1 のように,線分 AB を直径とする円Oの周上に,2 点 A,Bとは異なる点 C を,AC > BCとなるようにとる。また,円Oの周上に点Dを,∠CADが鈍角となるようにとり,線分ABと線分CDとの交点をEとする。さらに,線分CBの延長上に点Fを,CF=DFとなるようにとり,線分DFと円Oとの交点をG,線分AGと線分BDとの交点をHとする。
このとき、次の(ⅰ)(ⅱ)に答えなさい。
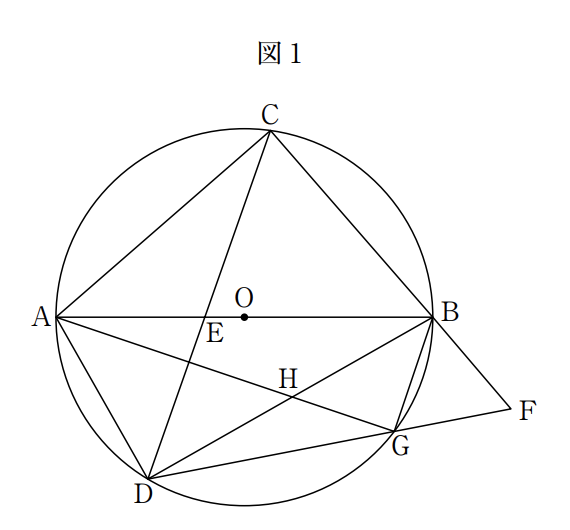
(ⅰ)三角形 ACE と三角形 AGD が相似であることを次のように証明した。(a) ,(b)に最も 適するものを,それぞれ選択肢の 1 ~ 4 の中から 1 つずつ選び,その番号を答えなさい。
[証明]
△ACEと△AGDにおいて,
まず,孤AD に対する円周角は等しいから,
∠ACD=∠AGD
よって,∠ACE=∠AGD ……①
次に,孤BDに対する円周角は等しいから,
(a) ……②
また,CF=DF より,△FCD は二等辺三角形で あり,その 2 つの底角は等しいから,
∠FCD=∠FDC
よって,∠BCD=∠CDG ……③
さらに,孤CG に対する円周角は等しいから,
(b) ……④
②,③,④より,
∠CAB=∠CAG-∠BAG
=∠BAD-∠BAG ……⑤
∠GAD=∠BAD-∠BAG ……⑥
⑤,⑥より,∠CAB=∠GAD
よって,∠CAE=∠GAD ……⑦
①,⑦より,2 組の角がそれぞれ等しいから,
△ACE∽△AGD
(a)の選択肢
1:∠ABC=∠ADC
2:∠AED=∠BEC
3:∠BAC=∠BDC
4:∠BAD=∠BCD
(b)の選択肢
1:∠AHC=∠BHG
2: ∠BAG=∠BDG
3:∠CAG=∠CDG
4:∠DAG=∠DBG
(ⅱ)次の[]の中の「あ」「い」「う」にあてはまる数字をそれぞれ 0 ~ 9 の中から 1 つずつ選び,そ の数字を答えなさい。
BC=4 cm,BG=FG=2 cm のとき,三角形 ADH の面積は[あ]√[い]/[う]cm²である。
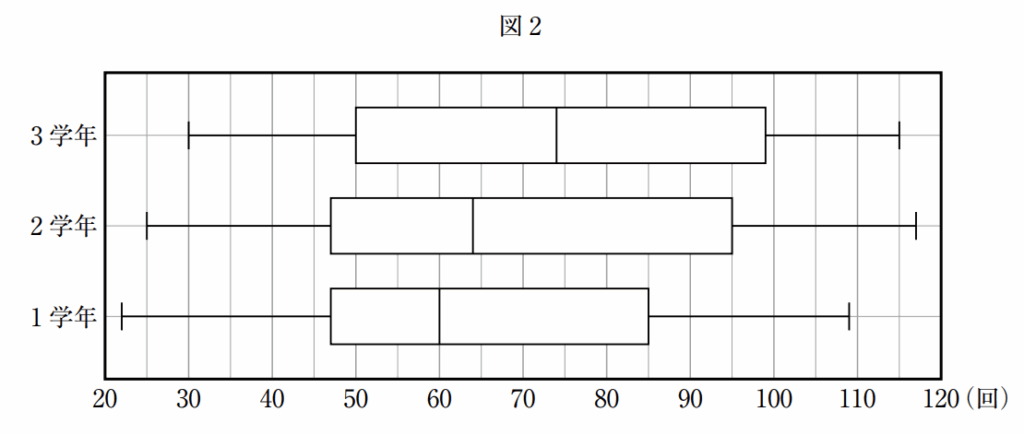
(イ)ある中学校で毎年開催されている縄跳び大会は,生徒ひとりひとりが1分間に縄跳びを何回跳べるか に挑み,跳んだ回数を競うものである。参加した3年生のAさん,2年生のBさん,1年生のCさん は,この大会の実行委員であり,今年の大会の結果について振り返っている。次の会話文はそのときのものである。 また,図2は,参加した生徒それぞれの,今年の大会で跳んだ回数を調べ,学年ごとに箱ひげ図に表 したものであり,学年ごとの参加人数は,3年生が 100人,2年生が110人,1年生が120人だった。 このとき,Aさん,Bさん,Cさんを,跳んだ回数が多い順に左から並べたものとして最も適するも のを 1 ~ 6 の中から 1 つ選び,その番号を答えなさい。
会話文
Aさん 「縄跳び大会の結果が出ましたね。私は学年で 21位でした。3年間で記録を伸ばすこ とができたので,本当にうれしいです。」
Bさん 「よかったですね。私は学年で28位でした。練習のときよりも多く跳べたので満足し ています。Cさんはどうでしたか。」
Cさん 「私は学年で 5 位で,目標にしていた 100 回を超えることができました。ただ,1年生 だけでなく2年生,3 年生も含めると,48人の生徒が私より多く跳んでいたそうなの で,さらに多く跳べるように頑張りたいと思いました。」
Aさん 「C さんの意欲はすごいですね。ちなみに,私と同じ回数だった生徒は校内に誰もいな かったそうです。」
Bさん 「そうなんですね。2年生の中には,私より1回多く跳び,学年で23位だった生徒が5人いましたよ。」
Cさん 「そんなこともあるんですね。来年はどうなるでしょうか。早くも来年の大会が楽しみ になってきました。来年は運営にももっと積極的に関わっていきたいです。」
Aさん 「来年の大会をよりよくしていくためにできることを一緒に考えていきましょう。」
1:Aさん,Bさん,Cさん
2:Aさん,Cさん,Bさん
3:Bさん,Aさん,Cさん
4:Bさん,Cさん,Aさん
5:Cさん,Aさん,Bさん
6:Cさん,Bさん,Aさん
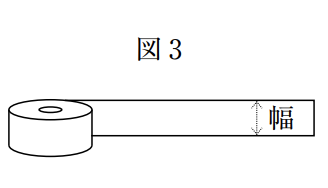
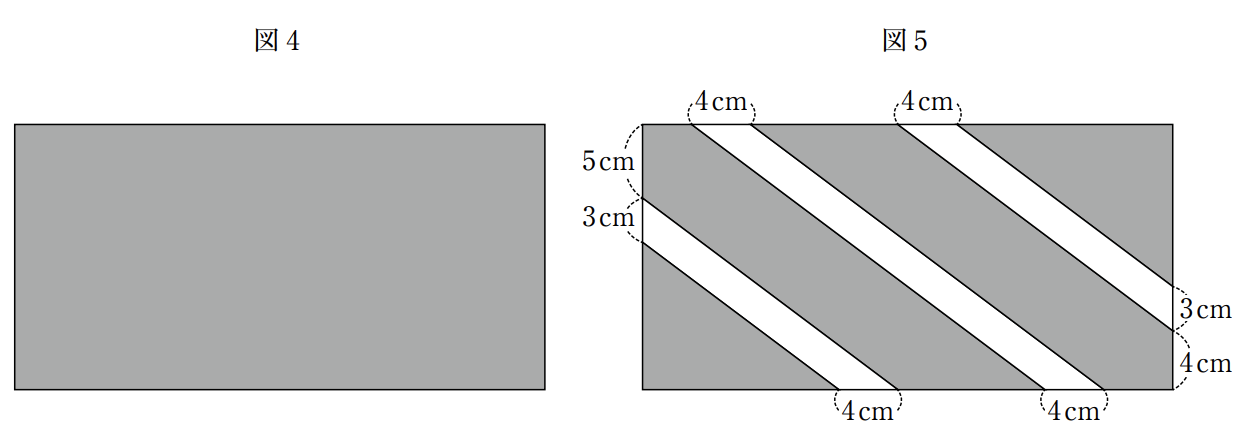
(ウ)右の図3のような幅が一定の白いテープと,下の図4のような横の 長さが縦の長さの2倍である長方形の色画用紙がある。長方形の色画 用紙に,このテープを途中で曲がらないようにして3か所に貼り,色画用紙の縁に沿ってテープを切ったところ,下の図5のようになった。 図5において,色画用紙のうち,テープを貼っていない部分の面積は480cm²だった。
Kさんは,この色画用紙の横の長さを次のように求めた。(ⅰ),(ⅱ)にあてはまるものとして最も適するものを,それぞれの選択肢の中から1つずつ選び,その番号を答えなさい。
求め方
色画用紙の縦の長さを x cm として方程式をつくると,
(ⅰ)=480
となる。
この方程式を解き,解が問題に適しているかどうかを確かめることで,色画用紙の縦の長さを求 めることができる。
色画用紙の横の長さは縦の長さの 2 倍であるから,色画用紙の横の長さは(ⅱ)cmである。
(ⅰ)の選択肢
1:x²-6x-7
2:x²-6x+24
3:2x²-12x-14
4:2x²-12x+48
5:2x²-8x+38
6:2x²-8x+96
(ⅱ)の選択肢
1:32
2:34
3:36
4:38
(エ)次の[ ]の中の「え」「お」にあてはまる数字をそれぞれ 0 ~ 9 の中から 1 つずつ選び,その数字を答えなさい。
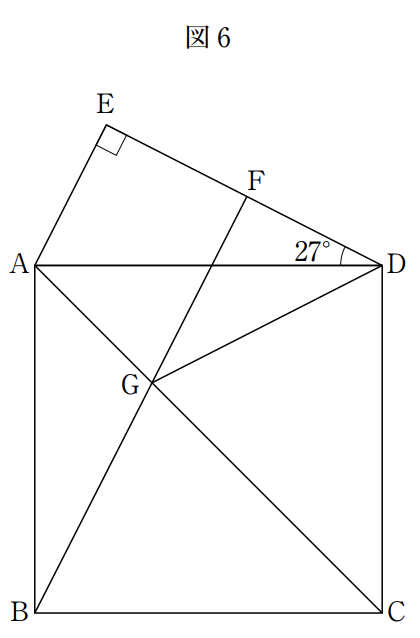
右の図6において,四角形ABCDは正方形であり,三角形 ADE は∠ADE=27°,∠AED=90°の直角三角形である。 また,点Fは線分DE上の点で,AE BF であり,点Gは 線分 AC と線分 BF との交点である。
このとき,∠CGD= [えお]°である。
(ア)(ⅰ)(a)4(b)3
(ア)(ⅱ)$\frac{7\sqrt{3}}{3}$
難問です。
四角形CDGBは円に内接する四角形なので
内閣はその対角の外角に等しいので∠CDG=∠GBF
二等辺GBFの底角で、∠GFB=∠GBF
∠BCD=∠FBGに注目すると、同位角が等しいのでCD//BG
∠CDG=∠BGF=∠GBFより、△BGFは正三角形だと分かります。
BからGFに垂線を下ろし、交点をIとします。
△BGIでは辺の比が1:2:√3から、GI=1cm、BI=√3cm
△BDIで三平方を用いるとBD=2√7cm
半円の弧に対する円周角より、∠ADB=90°
△BADと△BGIは相似で△BADも1:2:√3になります。
よって、$AD=2\sqrt{7}\times\frac{1}{\sqrt{3}}=\frac{2\sqrt{21}}{3}$cm
AGとCDの交点をJとして、△BGHと△DJHに注目します。
BG//CDの錯角で、∠DJH=90°
△GJDは内角が∠GBFの大きさと90°なので、1:2:√3より、DJ=2cm
錯角とDJ=BGから合同だと分かります。
BH=DHより、HはBDの中点だと分かります。
これらより△ADHの面積は$2\sqrt{7}\times\frac{2\sqrt{21}}{3}\div2\div2=\frac{7\sqrt{3}}{3}$
(イ)2
2年生の四分位数は上位55人の真ん中なので、28番目でありBさんの順位と同じです。
図2より95回であると分かります。これでCさん>Bさんがわかりました。
全学年でCさんの上には48人いることから48人の内訳に注目します。
1年生でCさんより上には4人。2年生はBさんの1つ上の23位が96回なので、100回飛んだCさんよりも少ないので、Cさんより上は22人。
つまり、3年生では$48-(4+22)=22$人いることが分かります。
ここで、Aさんは3年の21位で重複はなかったということからCさんよりも順位が上だと分かります。
よって、Aさん>Cさん>Bさんだと分かります。
(ウ)(ⅰ)4
真ん中のテープは4cm短い長方形と処理ができるので、縦$x$cm、横$2x-4$cmの長方形の中で考えます。
直角三角形と平行四辺形に分けて考えます。
直角三角形の面積は$3\times4\div2=6cm^2$
よって、テープの張っていない面積は$x(2x-4)-{4(x-8)+6+4(x-7)+6}=2x^2-12x+48$
(ウ)(ⅱ)3
方程式を解くだけです。
$2x^2-12x+48=480$
$x^2-6x-216=0$
$(x+12)(x-18)=0$
x>0なので、$x=18$
よって、横の長さは$18\times2=36cm$となります。
(エ)72°
AE//BFより、∠AED=∠BFD=90°
すると、∠GBC=$180-(90+27)=63°$
△BCGと△DCGに注目します。
ACは正方形の対角線なので、∠BCG=∠DCG=45°
正方形なのでBD=DC、GCが共通なので、合同だと分かります。
よって、∠CGD=∠CGB=$180-(63+45)=72°$となります。
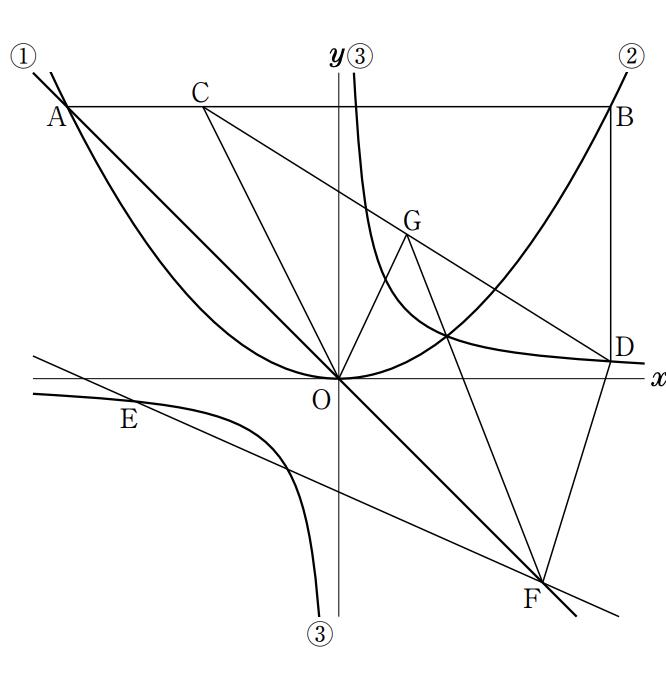
右の図において,直線①は関数y=-x のグラフであり,曲線②は関数 y=ax²のグラフ,曲線③は関数 y=4/xのグラフ である。
点Aは直線①と曲線②との交点 で,そのx座標は-8で あ る。 点Bは 曲線②上の点で, 線 分ABは x 軸に平行である。点Cは線分AB上の点で,AC:CB=1:3である。
また,点Dは曲線③上の点で,線分BDはy 軸に平行である。点Eは曲線③上の点で,そのx 座標は-6である。
さらに,原点をOとするとき,点Fは 直線①上の点で,AO:OF=4:3であ り,そのx 座標は正である。
このとき,次の問いに答えなさい。
(ア)曲線②の式 y=ax²のaの値として正しいものを次の 1 ~ 6 の中から 1 つ選び,その番号を答えなさ い。
1:a=1/8 2:a=1/6 3:a=1/4
4:a=3/8 5:a=1/2 6:a=3/4
(イ)直線EFの式を y=m x+n とするときの(ⅰ)m の値と,(ⅱ)n の値として正しいものを,それぞれ次 の 1 ~ 6 の中から 1 つずつ選び,その番号を答えなさい。
(ⅰ)mの値
1:m=-4/3 2:m=-7/6 3:m=-8/9
4:m=-5/6 5:m=-2/3 6:m=-4/9
(ⅱ)nの値
1:n =-16/3 2:n =-9/2 3:n =-4
4:n =-7/2 5:n =-10/3 6:n =-3
(ウ)次の[ ]の中の「か」「き」「く」「け」にあてはまる数字をそれぞれ 0 ~ 9 の中から 1 つずつ選び,その数字を答えなさい。
線分CD上に点Gを,CG=GDとなるようにとる。このときの,三角形COGと三角形DGFの面 積の比を最も簡単な整数の比で表すと,△COG:△DGF= [かき]:[くけ]である。
(ア)1
点Aのx座標が$-8$から➀に代入して$A(-8,8)$となります。
この点は➁も通るので代入すると、$64a=8$
$a=\frac{1}{8}$
(イ)(ⅰ)6 (ⅱ)5
点Eと点Fの座標が分かれば連立方程式を解くことで求まります。
点Eはx座標が$-6$から➀に代入して$A(-6,-\frac{2}{3})$となります。
AO:OF=4:3から$F(6,-6)$となります。
よって、$m=-\frac{4}{9},n=-\frac{10}{3}$となります。
(ウ)【か】2【き】2【く】3【け】1
△COGと△DGFはCG=GDで底辺が同じ大きさなので、面積比はIO:KFの比になります。
$BD=8-\frac{1}{2}=\frac{15}{2}$
△BCD∽△HCIより、$HI=\frac{15}{2}\times\frac{4}{12}=\frac{5}{2}$
よって、$IO=8-\frac{5}{2}=\frac{11}{2}$
△BCD∽△JCKより、$JK=\frac{15}{2}\times\frac{10}{12}=\frac{25}{4}$
よって、$KF=(8+6)\frac{25}{4}=\frac{31}{4}$
これらより、$△COG:△DGF=\frac{11}{2}:\frac{31}{4}=22:31$
図 1のように,30gのおもりが8個,50gのおもりが7個,80g のおもりが 1 個ある。
大,小 2 つのさいころを同時に1回投げ,大きいさいころの出た目の数をa,小さいさいころの出た目の数をbとする。
さいころの出た目の数によって,KさんとLさんは,次の【ルール】にしたがってこれらのおもりを取り分ける。それぞれが取ったおもりをすべてはかりにのせ,計測した重さについて考える。

【ルール】 まず,Kさんは30gのおもりを a 個と50gのおもりを b個取り,Lさんは残った30gのおもりと50gのおもりをすべて取る。
次に,KさんとLさんのうち,30gのおもりと50gのおもりを合わせた個数の少ない方が80gのおもりを取る。
例
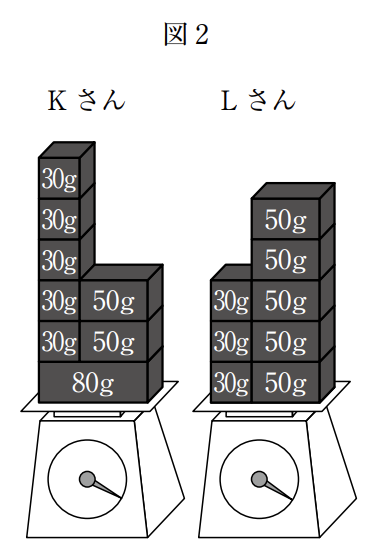
大きいさいころの出た目の数が 5,小さいさいころの出た目の数が 2 のとき,a=5,b=2 である。
【ルール】により,まず,Kさんは30gのおもりを5個,50gのおもりを 2 個取り,Lさんは残った30gのおもりと50gのおもりをすべて取るので,30g のおもりを3個,50gのおもりを5個取る。
次に,30gのおもりと50gのおもりを合わせた個数は,Kさんが 7 個,Lさんが8個なので,合わせた個数の少ないKさんが80gのおもりを取る。
それぞれが取ったおもりをすべてはかりにのせると図2のようになり,Kさんの計測した重さは330g,Lさんの計測した重さは340gとなる。
いま,図1の状態で,大,小2つのさいころを同時に1回投げるとき,次の問いに答えなさい。ただ し,大,小2つのさいころはともに,1から6までのどの目が出ることも同様に確からしいものとする。
(ア)次の[ ]の中の「こ」「さ」「し」にあてはまる数字をそれぞれ 0 ~ 9 の中から 1 つずつ選び,その数字を答えなさい。
K さんの計測した重さが 200g 未満となる確率は[こ]/[さし]である。
(イ)次の の中の「す」「せ」「そ」「た」にあてはまる数字をそれぞれ 0 ~ 9 の中から 1 つずつ選び,
その数字を答えなさい。
Kさんの計測した重さがLさんの計測した重さより重くなる確率は[すせ]/[そた]である。
(ア) 【こ】1【さ】1【し】8
Kさんの重さが200g未満となるためには必ず80gのおもりを取らないといけない。
つまり、30gと50gのおもりが$200-80=120g$未満になる組み合わせしかなく、これは(a,b)=(1,1),(2,1)の2通りしかない。
全通りは36通りなので、確率は$\frac{2}{36}=\frac{1}{2}$
(イ) 【す】1【せ】7【そ】3【た】6
80gのおもりを取るか取らないかで場合分けして考えます。
➀80gが無いとき
おもりを取る数は8個以上で、80gを含めたLよりも重さが多くないといけません。
よって、$(590+80)\div2=335g$以上になる組み合わせを考えます。
(ⅰ)b=6のとき
(a,b)=(2,6)(3,6)(4,6)(5,6)(6,6)の5通り
(ⅱ)b=5のとき
(a,b)=(3,5)(4,5)(5,5)(6,5)の4通り
(ⅲ)b=4のとき
(a,b)=(5,4)(6,4)の2通り
よって、11通りあります。
➁80gがあるとき
おもりを取る数は7個以下で、$335-80=255g$以上になる組み合わせを考えます。
(ⅰ)b=6のとき
(a,b)=(1,6)の1通り
(ⅱ)b=5のとき
(a,b)=(1,5)(2,5)の2通り
(ⅲ)b=4のとき
(a,b)=(2,4)(3,4)の2通り
(ⅳ)b=3のとき
(a,b)=(4,3)の1通り
よって、6通りあります。
これらより確率は$\frac{11+6}{36}=\frac{17}{36}$
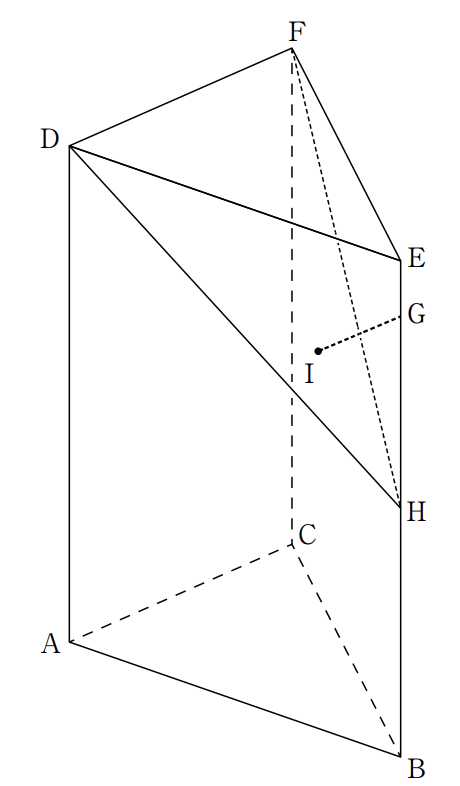
図1は,AB=BC=13 cm,AC=10 cm の二等辺三角形ABC を底面とし,AD=BE=CF=18 cm を高さとする三角柱である。
また,点Gは辺BE上の点で,BG:GE=8:1 であり,点Hは辺BEの中点である。
このとき,次の問いに答えなさい。
(ア)この三角柱の表面積として正しいものを次の1 ~ 6の中から1 つ選び,その番号を答えなさい。
1:468cm² 2:478cm² 3:648cm²
4:658cm² 5:768cm² 6:778cm²
(イ)次の[ ]の中の「ち」「つ」「て」にあてはまる数字をそれぞ れ 0 ~ 9 の中から 1 つずつ選び,その数字を答えなさい。
この三角柱において,図のように,点 G から 3 点 D,F,H を通る平面に引いた垂線と,3点 D,F,H を通る平面との交点をIとする。このときの,線分GIの長さは[ちつ]/[て]cmである。
(ア)5
表面積は底面積と側面積を求めればよい。
底面積:△ABCは二等辺三角形なので、垂線を下すとACの中点になるので、三平方の定理を使うと高さhが出て、$\sqrt{13^2-5^2}=12$
よって、$10\times12\div2=60cm^2$
側面積:3つの長方形を足し合わせればよいので、$18\times13+18\times10+18\times13=648cm^2$
よって、$60cm^2\times2+648cm^2=768cm^2$
(イ)【ち】2【つ】8【て】5
HはEBの中点なので、$EH=9cm$
BG:GE=8:1より、$EG=18\times\frac{1}{9}=2cm,GH=7cm$
面EHJで切り取ると、面ED⊥EBから、∠HEJ=90°
よって、△HEJ∽△HIG
HE:EJ=9:12=3:4より、辺の比が3:4:5になるので、
$GJ=7\times\frac{4}{5}=\frac{28}{5}cm$
家庭教師のやる気アシストは、神奈川県にお住まいの受験生のお子さんを毎年たくさん指導をさせ頂き、合格に導いています。
高い合格率の秘訣は、指導経験豊富な先生の指導力に加え、1対1の指導でお子さん一人ひとりの状況に合わせた、お子さんだけのカリキュラムで勉強が進められるから!
家庭教師のやる気アシストは、お子さんの志望校合格まで全力でサポートさせて頂きます!
お子さんにとって「成果が出る勉強法」ってどんな勉強法だと思いますか?
お子さんそれぞれに、個性や性格、学力の差もあります。そんな十人十色のお子さん全員に合う勉強法ってなかなかないんです。
たからこそ、受験生の今だけでもお子さんだけの勉強法で受験を乗り越えてみませんか?
やる気アシストには、決まったカリキュラムはありません。お子さんの希望や学力、得意や不得意に合わせて、お子さんだけのカリキュラムで指導を行っていきます。また、勉強法もお子さんそれぞれに合う合わないがあります。無料体験授業では、お子さんの性格や生活スタイルを見せていただき、お子さんにとって効率的な成果の出る勉強のやり方をご提案させて頂きます。

