







千葉県の2023年3月実施の令和5年度(2023年度)入学者の公立高校入試問題の解説をしています。
受験勉強において、過去問を解くことはとても効果的な勉強法です。ぜひ、受験までに一度挑戦し、問題の傾向を掴んでおきましょう。合わせて、対策などをたてられるととても良いですね。
また、過去問で苦手な点が見つかった場合は、そこを中心に試験日当日までにしっかりと対策しておきましょう。
次の(1)~(7)の問いに答えなさい。
(1)次の①~③の計算をしなさい。
①$6\div(-2)-4$
②$a+b+\frac{1}{4}(a-8b)$
③$(x-2)^2+3(x-1)$
(2)次の①、②の問いに答えなさい。
①$5x^2-5y^2$を因数分解しなさい。
②$x=\sqrt{3}+2,y=\sqrt{3}-2$のとき、$5x^2-5y^2$の値を求めなさい。
(3)下の資料は、ある中学生の生徒240人のスポーツテストにおけるシャトルランの結果を表した度数分布表と箱ひげ図である。
このとき、次の①、②の問いに答えなさい。
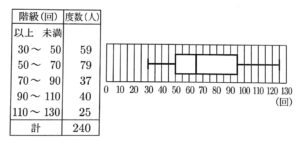
①90回以上110回未満の階級の相対度数を求めなさい。
ただし、小数第3位を四捨五入して、小数第2位まで求めること。
②資料から読み取れることとして正しいものを、次のア~エのうちから1つ選び、符号で答えなさい。
ア 範囲は100回である。
イ 70回以上90回未満の階級の累積度数は102人である。
ウ 度数が最も少ない階級の階級値は120回である。
エ 第3四分位数は50回である。
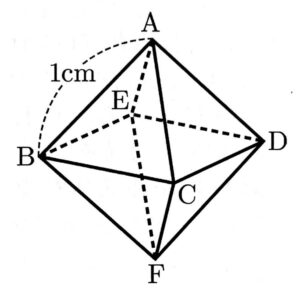
(4)次の図のように、点A,B,C,D,E,Fを頂点とする1辺の長さが1cmの正八面体がある。
このとき、次の①、②の問いに答えなさい。
①線分BDの長さを求めなさい。
②正八面体の体積を求めなさい。
(5)下の図のように、1,3,4,6,8,9の数字が1つずつ書かれた6枚のカードがある。この6枚のカードをよく切って、同時に2枚引く。
このとき、次の①、②の問いに答えなさい。ただし、どのカードを引くことも同様に確からしいものとする。
①ひいた2枚のカードに書かれた数が、どちらも3の倍数である場合は何通りあるか求めなさい。
②ひいた2枚のカードに書かれた数の積が、3の倍数だる確率を求めなさい。
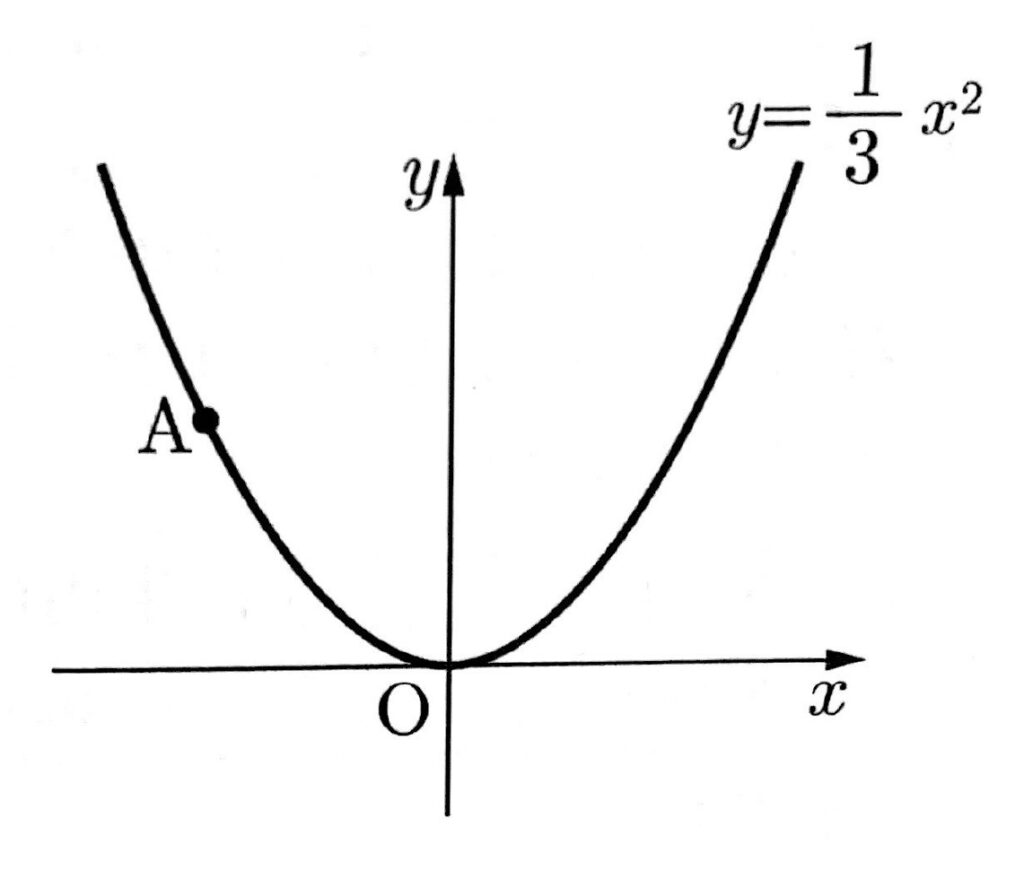
(6)次の図のように、関数$y=\frac{1}{3}x^2$のグラフ上に点Aがあり、点Aのx座標は-3である。このとき、次の①、②の問いに答えなさい。
①点Aのy座標を求めなさい。
②関数$y=\frac{1}{3}x^2$について、xの変域が$-3\leqq x \leqq a$のとき、yの変域が$0\leqq y \leqq 3$となるような整数aの値を全て求めなさい。
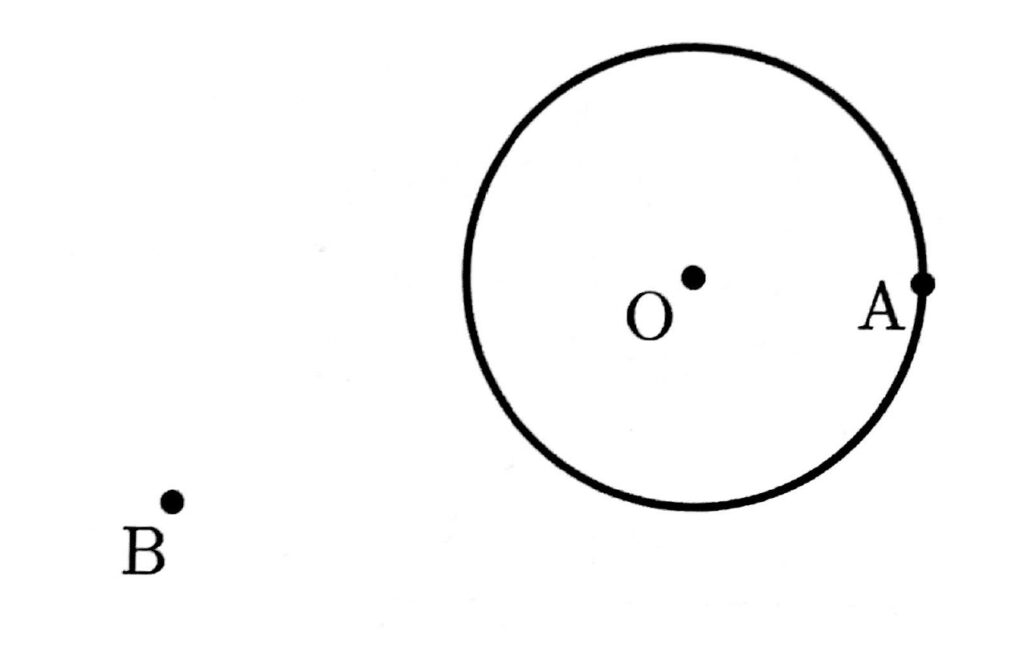
(7)次の図のように、点Oを中心とする円Oとその外部の点Aがあり、円Oの外部に点Bがある。点Aを接点とする接線と、点Bから円Oにひいた2本の接線との交点P,Qを作図によって求めなさい。なお、AP>AQであるとし、点Pと点Qの位置を示す文字PとQも書きなさい。
ただし、三角定規の角を利用して直線をひくことはしないものとし、作図に用いた線は消さずに残しておくこと。
(1)①$-7$ ②$\frac{5}{4}a-b$ ③$x^2-x+1$
①$6\div(-2)-4=-3-4=-7$
②$a+b+\frac{1}{4}(a-8b)=a+b+\frac{1}{4}a-2b=\frac{5}{4}a-b$
③$(x-2)^2+3(x-1)=x^2-4x+4+3x-3=x^2-x+1$
(2)①$5(x+y)(x-y)$ ②$40\sqrt{5}$
①$x^2-y^2=(x+y)(x-y)$の公式に当てはめればよい。
$5x^2-5y^2=5(x+y)(x-y)$
②先に$x+y$と$x-y$を計算しておくとよい。
$x+y=(\sqrt{3}+2)+(\sqrt{3}-2)=2\sqrt{3}$
$x-y=(\sqrt{3}+2)-(\sqrt{3}-2)=4$
よって、$5x^2-5y^2=5(x+y)(x-y)=5\times 2\sqrt{3} \times 4=40\sqrt{3}$
(3)①$0.17$ ②ウ
①相対度数は「その階級の度数」÷「全体」で求めることができるので
$40\div240=0.166\fallingdotseq0.17$
②
ア:箱ひげ図より、範囲は$125-30=95\ne100$なので不適。
イ:度数分布表より、70回以上90回未満の階級の累積度数は、$59+79+37=175\ne102$なので不適。
ウ:度数分布表より、度数が最も少ない階級は、110回以上130回未満で、その階級値は$\frac{110+130}{2}=120$なので適する。
エ:箱ひげ図より、第3四分位数は$95\ne50$なので不適。
(4)①$\sqrt{2}cm$ ②$\frac{\sqrt{2}}{3}cm^3$
①三角形ABDに注目すると、$1:1:\sqrt{2}$の比になる三角形になっているので、$BD=\sqrt{2}cm$
②体積が分かるためにはA-BEFCの高さが分かればよい。Aからの垂線と正方形BCDEの交点をHとすると、
ABHは$1:1:\sqrt{2}$の比になる三角形になっているので、$AH=\frac{\sqrt{2}}{2}cm$である。
よって、体積は$BC \times CD \times AH \times \frac{1}{3} \times 2=1 \times 1 \times \frac{\sqrt{2}}{2} \times \frac{1}{3} \times 2=\frac{\sqrt{2}}{3}cm^3$
(5)①3通り ②$\frac{4}{5}$
ひいた2枚のカードに書かれた数の組を$(a,b) (a<b)$とする。
①どちらも3の倍数である場合は$(a,b)=(3,6),(3,9),(6,9)$の3通り。
②すべての通りは$5+4+3+2+1=15$通り。
積が3の倍数になるときは、どちらか一方が3の倍数であればよいので
$(a,b)=(1,3),(1,6),(1,9),(3,4),(3,6),(3,8),(3,9),(4,6),(4,9),(6,8),(6,9),(8,9)$の12通り。
よって、確率は$\frac{12}{15}=\frac{4}{5}$が答えとなる。
(6)①$y=3$ ②$a=0,1,2,3$
①$y=\frac{1}{3}x^2$の式に、$x=-3$を代入すればよい。
②yの変域の最小値が0であることから、aの最小値は0だと分かる。
次にyの変域の最大値が3であることから、aの最大値は3だと分かる。
(7)下図参照
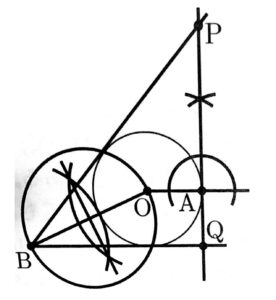
点Aを接点とする円Oの接線は、点Aを通り直線OAに垂直な直線。
点Bから円Oにひいた2本の接線は、線分BOの中点を中心として2点B,Oを通る円と円Oとの2つの交点と、点Bをそれぞれ結ぶ2本の直線。
次の図のように、直線$y=4x$上の点Aと。直線$y=\frac{1}{2}x$上の点Cを頂点にもつ正方形ABCDがある。点Aと点Cのx座標が正で、辺ABがy軸と平行であるとき、次の(1),(2)の問いに答えなさい。
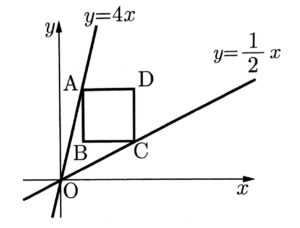
(1)点Aのy座標が8であるとき、次の①、②の問いに答えなさい。
①点Aのx座標を求めなさい。
②2点A,Cを通る直線の式を求めなさい。
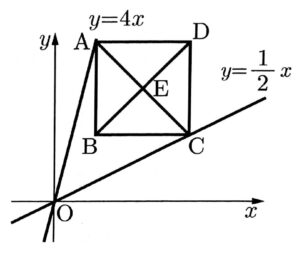
(2)正方形ABCDの対角線ACと対角線BDの交点をEとする。点Eのx座標が13であるとき、点Dの座標を求めなさい。
(1)①$x=2$ ②$y=-x+10$
①直線$y=4x$に$y=8$を代入すればよい。
②$AB//y軸,AB=AC$だから、直線ACの傾きは$-1$
よって、$y=-x+b$
A(2,8)を代入して、$b=10$
したがって、$y=-x+10$
(2)D(20,24)
正方形ABCDの1辺の長さを$2a$とする。
点Cと点Aの座標を求めれば、点Cのx座標と点Aのy座標がそれぞれ点Dの座標となる。
点Cを求めるために点EがBCの中点になるので
$点C(13+a,\frac{13+a}{2})$と表せる。
同様に$点A(13-a,4(13-a))$と表せる。
よって、点Dは$(13+a,4(13-a))$となる。
DCの長さが2aになることに注目すると$4(13-a)-\frac{13+a}{2}=2a$という式が立つ。
これを解くと、$a=7$となるので、$点D(20,24)$
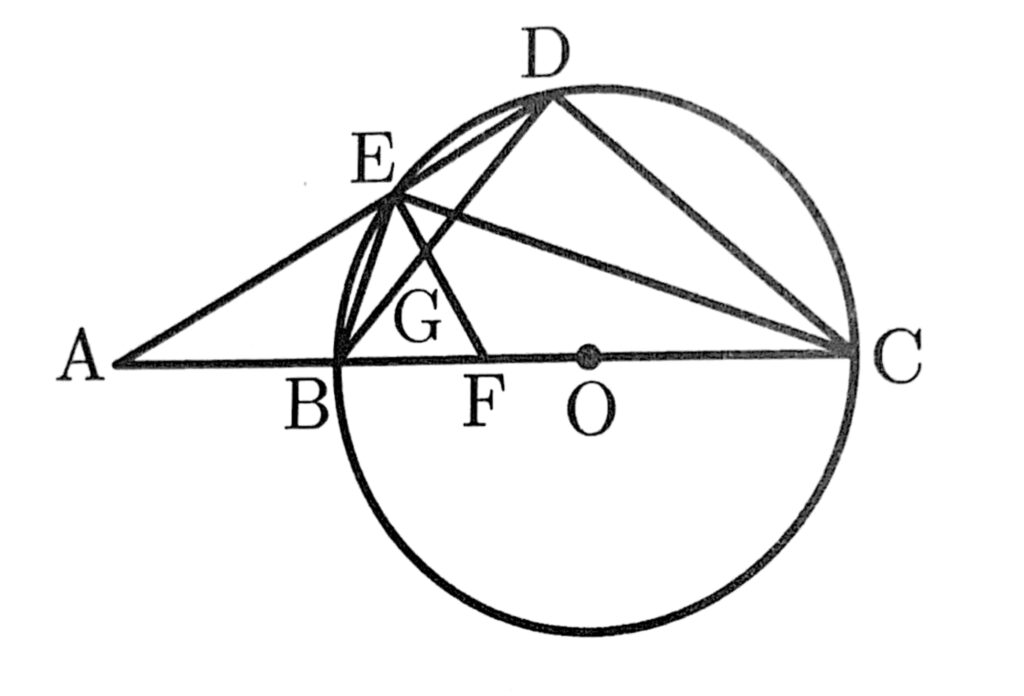
次の図のように、点Oを中心とする円Oとその外部の点Aがある。直線AOと円Oとの交点のうち、点Aに近い方を点B、もう一方を点Cとする。円Oの円周上に、2点B,Cと異なる点Dを、線分ADと円Oが点D以外の点でも交わるようにとり、その交点を点Eとする。また、点Bと点D、点Bと点E、点Cと点D、点Cと点Eをそれぞれ結ぶ。
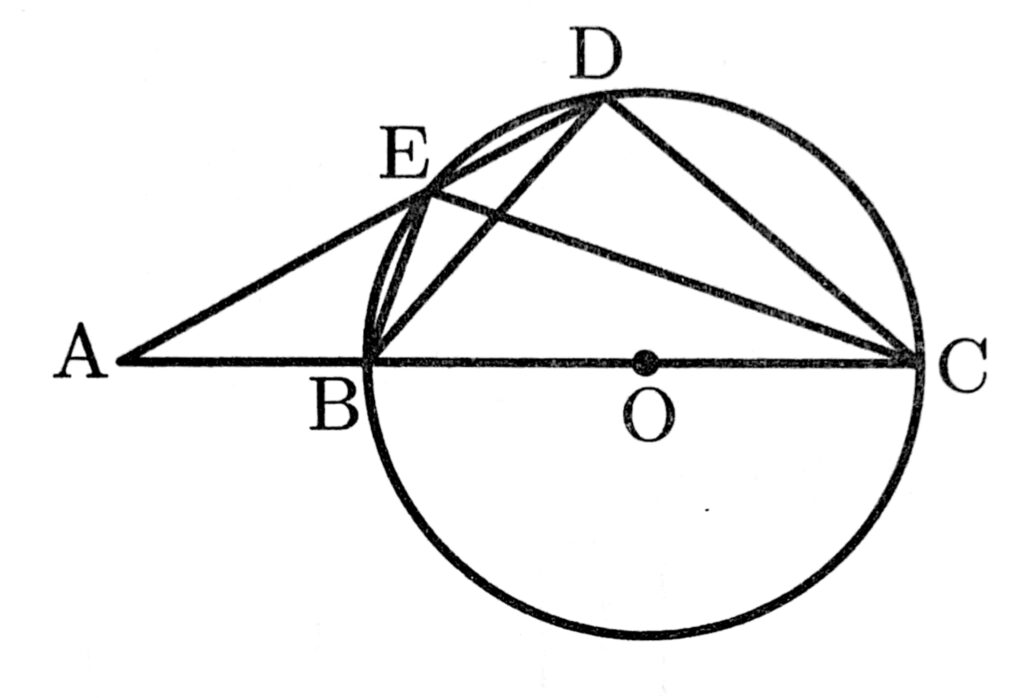
このとき、次の(1)~(3)の問いに答えなさい。
(1)次の【a】【b】に入る最も適当なものを、選択肢のア~エのうちからそれぞれ1つずつ選び、符号で答えなさい。また、【c】に入る最も適当な数を書きなさい。
【a】と【b】は半円の弧に対する円周角だから、いずれも【c】度である。
選択肢
ア ∠EBC イ ∠BEC ウ ∠DCB エ ∠BDC
(2)△ABE∽△ADCとなることを証明しなさい。
ただし、(1)のことがらについては、用いてもかまわないものとする。
(3)点Eを通る線分ADの垂線をと線分ACとの交点を点Fとし、線分EFと線分BDの交点を点Gとする。
EG=1cm,GF=2cm,∠A=30°であるとき、線分ABの長さを求めなさい。
(1)【a】イ【b】エ【c】90
直径の円周角は90°になる。【a】と【b】は順不同。
(2)【解答例】
△ABEと△ADCにおいて
共通な角なので∠BAE=∠DAC…①
図より
∠ACD=∠ECB+∠DCB…②
また、同じ弧に対する円周角は大きさは等しいので
∠ECB=∠EDB,∠DCB=∠DBE…③
△BEDに注目すると、外角の性質より
∠AEB=∠EDB+∠DBE…④
➂より、∠AEB=∠ACD…⑤
①、⑤より2組の角がそれぞれ等しいので
△ABE∽△ADCである。
(3)$AB=6-\sqrt{6}cm$
AB=AF-BFで求めることをゴールに置く。
△AFEに注目すると、∠A=30°、∠F=60°、∠E=90°の形なので
$AF=2EF=6(cm)$
次に、BFを求めるために、△BFGと△EFBに注目する。
共通な角なので
∠BFG=∠EFB…①
∠FBG=∠CBD…②
同じ弧に対する円周角は大きさは等しいので
∠CBD=∠CED…③
②、③より、∠FBG=∠CED…④
∠FEB=∠BEC-∠FEC=90°-∠FEC…⑤
∠CED=∠FED-∠FEC=90°-∠FEC…⑥
⑤、⑥より、∠FEB=∠CED…⑦
➃、⑦より、∠FBG=∠FEB…⑧
①、⑧より、2組の角がそれぞれ等しいので
△BFG∽△EFB
よって、BF:EF=FG:FB
$BF^2=EF \times FG =6$
$BF=\sqrt{6}$
よって、$AB=6-\sqrt{6}$
2人でじゃんけんをして、次のルールにしたがって点数を競うゲームがある。このゲームについて、下の会話文を読み、あとの(1)(2)の問いに答えなさい。
ルール
・じゃんけんを1回するごとに、勝った人は出した手に応じて加点され、負けた人は出した手に応じて減点される。
・グーで勝つと1点、チョキで勝つと2点、パーで勝つと5点が加点される。
・グーで負けると1点、チョキで負けると2点、パーで負けると5点が減点される。
・あいこの場合は1回と数えない。
・最初の持ち点は、どちらも0点とする。
会話文
生徒X:例えば, AさんとBさんが1回じゃんけんをして、Aさんがチョキ, Bさんがパーを出したとき、それぞれの持ち点は, Aさんが2点, Bさんが5点になるということでしょうか。
教師T:そうですね。 では, AさんとBさんが3回じゃんけんをして,次のような手を出した結果, Aさんの持ち点は何点になるでしょうか。
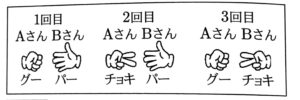
生徒X:(a)点です。
教師 T : そのとおりです。 それでは、2人がどのような手を出したのかがわからない場合を考えてみましょう
AさんとBさんが3回じゃんけんをして, Aさんが2回勝ち、Bさんが1回勝った結果,Aさんの持ち点が9点だったとき, Bさんの持ち点を求めてみましょう。
生徒X:まず, Aさんが勝った2回の加点の合計を考えます。例えば,2回ともグーで勝った場合は加点の合計が2点となり, グーとチョキで勝った場合は加点の合計が3点となります。 このように考えていくと,勝った2回の加点の合計は全部で(b)通り考えることができます。
このうち, Aさんが負けた1回の減点を考えた上で,3回じゃんけんをした結果, Aさんの持ち点が9点となりうる場合は1通りのみです。
このことから,3回じゃんけんをした結果, Bさんの持ち点が(c) 点となることがわかります。
教師 T:そうですね。 じゃんけんの回数が少なければ,1つずつ考えることができますね。
では、回数が多くなった場合について考えてみましょう。
下の表は、じゃんけんを1回だけしたときのAさんとBさんの手の出し方と、持ち点をまとめたものです。この表をみて気が付くことはありますか。
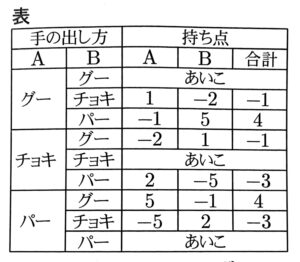
生徒 X:2人の手の出し方は3通りずつありますが、あいこの場合は1回と数えないため, 2人の手の出し方の組み合わせは,全部で6通り考えればよいということになります。
また、じゃんけんを1回だけした結果, A さんとBさんの持ち点の合計は,どちらかがグーで勝った場合は-1 点, どちらかがチョキで勝った場合は-3点,どちらかがパーで勝った場合は4点となっています。
教師 T:そうですね。 2人の持ち点の合計で考えると, 3通りになりますね。
では、AさんとBさんが10回じゃんけんをしたとき,どちらかがグーで勝った回数をa回どちらかがチョキで勝った回数をb回 どちらかがパーで勝った回数をc回とすると, cはaとbを使ってどのように表すことができるでしょうか。 また, 10回じゃんけんをした結果の2人の持ち点の合計をM点としたとき, Mをaとbを使って表すとどのようになりますか。
生徒X:c=(d),M=(e) と表すことができます。
教師T:そのとおりです。 2人の持ち点の合計について,この式を用いると,a とbとcの組み合わせがどのようになるのかが考えやすくなりますね。
(1)会話文中の(a)~(e)について、次の①、②の問いに答えなさい。
① (a),(b),(c)にあてはまる数を、それぞれ書きなさい。
② (d),(e)にあてはまる式を、それぞれ書きなさい。
ただし、(e)についてはcを使わずに表すこと。
(2)2人の持ち点の合計が0点となるときのa,b,cの組み合わせをすべて求めなさい。
ただし、答えを求める過程がわかるように、式やことばを使って説明しなさい。
(1)①(a)+2,(b)9,(c)+3
(a)Aさんの点数は$-1+2+1=+2$となる。
(b)$3 \times 3=9$通りとなる。
(c)Aさんの点数が9点になるのは2回パーで勝ち、1回グーで負けるときなので、
Bさんは2回グーで負け、1回パーで勝ったことになるので
$-1-1+5=+3$となる。
(1)②(d)$10-(a+b)$,(e)$40-5a-7b$
(d)$a+b+c=10$を変形すればよい。
(e)$(-1 \times a) + (-3 \times b) + (4 \times c )$に代入して求めればよい。
(2)【解答例】
$M=40-5a-7b=0$となるときの、$a,b$の値を求めればよい。
40が5の倍数であることから、7bが0または5の倍数となるときに成立すると考えられる。
よって、$b=0,5$が一意に決まる。
ここから、$(a,b,c)=(8,0,2),(1,4,5)$の2通りとなる。
家庭教師のやる気アシストは、千葉県にお住まいの受験生のお子さんを毎年たくさん指導をさせ頂き、合格に導いています。
高い合格率の秘訣は、指導経験豊富な先生の指導力に加え、1対1の指導でお子さん一人ひとりの状況に合わせた、お子さんだけのカリキュラムで勉強が進められるから!
家庭教師のやる気アシストは、お子さんの志望校合格まで全力でサポートさせて頂きます!
お子さんにとって「成果が出る勉強法」ってどんな勉強法だと思いますか?
お子さんそれぞれに、個性や性格、学力の差もあります。そんな十人十色のお子さん全員に合う勉強法ってなかなかないんです。
たからこそ、受験生の今だけでもお子さんだけの勉強法で受験を乗り越えてみませんか?
やる気アシストには、決まったカリキュラムはありません。お子さんの希望や学力、得意や不得意に合わせて、お子さんだけのカリキュラムで指導を行っていきます。また、勉強法もお子さんそれぞれに合う合わないがあります。無料体験授業では、お子さんの性格や生活スタイルを見せていただき、お子さんにとって効率的な成果の出る勉強のやり方をご提案させて頂きます。

