【北海道】令和5年度/2023年度入学者高校入試選抜試験：数学の解説
北海道の2023年3月実施の令和5年度（2023年度）入学者の公立高校入試問題の解説をしています。
受験勉強において、過去問を解くことはとても効果的な勉強法です。ぜひ、受験までに一度挑戦し、問題の傾向を掴んでおきましょう。合わせて、対策などをたてられるととても良いですね。
また、過去問で苦手な点が見つかった場合は、そこを中心に試験日当日までにしっかりと対策しておきましょう。
大問1
問題文
問1
（1）～（3）の計算をしなさい。
（1）$9 – (-5)$
（2）$(-3)^2 \div \frac{1}{6}$
（3）$\sqrt{2} \times \sqrt{14}$
問2
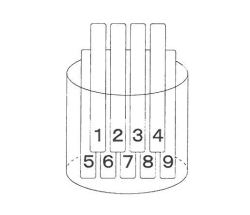
下の図のように、円筒の中に1から9までの数字が1つずつ書かれた9本のくじがあります。円筒の中から1本のくじを取り出し、くじに書かれた数が偶数のとき教室政争の担当に、奇数のとき廊下清掃の担当に決まるものとします。
Aさんが9本のくじの中から1本を取り出すとき、Aさんが教室清掃の担当に決まる確率を求めなさい。
問3
下の表は、ある一次関数について、$x$の値と$y$の値の関係を示したものです。表の【 】に当てはまる数を書きなさい。
| $x$ | … | -1 | 0 | … | 3 | … |
| $y$ | … | 6 | 【 】 | … | 2 | … |
問4
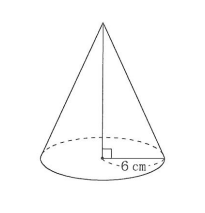
下の図のように、底面の半径が6cm、体積が132$\pi \text{ cm}^3$の円錐があります。
この円錐の高さを求めなさい。
問5
$x^2 – 【 】x + 14$ が $(x – a)(x – b)$ の形に因数分解できるとき、$【 】$ に当てはまる自然数を2つ書きなさい。ただし、$a, b$ はいずれも自然数とします。
問6
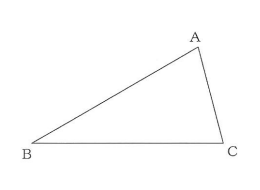
下の図のように、$\angle ACB=75°、BA=BC$の二等辺三角形ABCがあります。$\triangle ABC$の内部に点Pをとり、$\angle ACB=\angle PCB = 15°$となるようにします。点Pを定規とコンパスを使って作図しなさい。
ただし、点を示す記号Pをかき入れ、作図に用いた線は消さないこと。
解答・解説
問1
（1）14
（2）54
（3）$2\sqrt{7}$
$\sqrt{28}$ を整理した値が答え
問2 $\frac{4}{9}$
1から9までの中に偶数は4つある。つまり9本の中から2、4、6、8を選ぶ確率を求めれば良い。
問3 5
$x=-1, y=6$ と $x=3, y=2$ から2点を通る直線の式を求めると $y=-x+5$ になる。この式の切片の値が空欄に当てはまるため5が正解。
問4 11cm
円錐の体積は（底面積）$\times$（高さ）$\div 3$ で求められる。
問5 9、15
$a \times b$ が14になり、因数分解の式から $a+b$ が正になる組み合わせを考える。
$a=1、b=14$、$a=2、b=7$ が考えられる。それぞれの数値を代入して展開し、式を比較すると空欄に9、15が当てはまる。
問6
$\angle ACB=75^\circ$で、二等辺三角形の性質を用いると$\angle ABC=30^\circ$になる。$\angle ABC=30^\circ$の角の二等分線を引くとその直線上に点Pがあることがわかる。更に線分BCの首位直二等分線を引きそれと角の二等分線の交点が点Pになる。
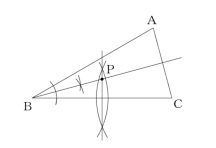
$\angle ACB=75^\circ$で、二等辺三角形の性質を用いると$\angle ABC=30^\circ$になる。
$\angle ABC=30^\circ$の角の二等分線を引くとその直線上に点Pがあることがわかる。更に線分BCの首位直二等分線を引きそれと角の二等分線の交点が点Pになる。
大問2
問題文
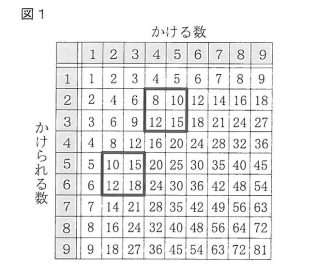
図1のような、小学生で学習したかけ算九九の表があります。優さんは、太線で囲んだ数のように、縦横に隣り合う4つの数について、左上を「$a$」、右上を「$b$」、左下を「$c$」、右下を「$d$」としたとき、4つの数の和$a+b+c+d$がどんな数になるかを考えています。
【例えば】
・左上が「8」、右上が「10」、左下が「12」、右下が「15」のとき、8+10+12+15=45
・左上が「10」、右上が「15」、左下が「12」、右下が「18」のとき、10+15+12+18=55
優さんは、45=5×9、55=5×11となることから、次のように予想しました。
（予想Ⅰ）
縦横に隣り合う4つの数の和は、5の倍数である。
問1
予想Ⅰが正しいとは言えないことを、次のように説明するとき、【 ア 】～【 オ 】に当てはまる数を、それぞれ書きなさい。
（説明）
縦横に隣り合う4つの数が$a$ =【 ア 】、$b$ =【 イ 】、$c$ =【 ウ 】、$d$ =【 エ 】のとき、4つの数の和、$a+b+c+d$ は、【 オ 】となり、5の倍数ではない。したがって、縦横に隣り合う4つの数の和は、5の倍数であるとは限らない。
問2
優さんは、予想Ⅰがいつでも成り立つとは限らないことに気づき、縦横に隣り合う4つの数それぞれの、かけられる数とかける数に注目して、あらためて調べ、予想をノートにまとめました。
（優さんのノート）
（予想Ⅱ）
縦横に隣り合う4つの数の和は、（かけられる数の和）×（かける数の和）である。
予想Ⅱがいつでも成り立つあことを、次のように説明するとき、【 ア 】～【 キ 】に当てはまる式を、それぞれ書きなさい。
（説明）
$a$を、かけられる数$m$、かける数$n$の積として$a=mn$とすると、$b$、$c$、$d$は、それぞれ$m$、$n$を使って、$b$ =【 ア 】、$c$ =【 イ 】、$d$ =【 ウ 】と表すことができる。
このとき、4つの数の和 $a+b+c+d$ は、
$a+b+c+d=mn+【 ア 】+【 イ 】+【 ウ 】$
=$4mn+2m+2n+1$
=$(2m+1)(2n+1)$
={【 エ 】+（【 オ 】）}{【 カ 】+（【 キ 】）} となる。
したがって、縦横に隣り合う4つの数の和は、（かけられる数の和）×（かける数の和）である。
問3
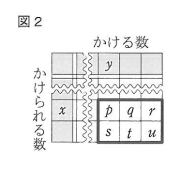
優さんは、図2の太線で囲んだ数のように、縦横に隣り合う6つの数の和について調べてみたところ、縦横に隣り合う6つの数の和も、（かけられる数の和）×（かける数の和）となることが分かりました。図2において、$p+q+r+s+t+u=162$ となるとき、$p$のかけられる数$x$、かける数$y$の値を、それぞれ求めなさい。
問3
優さんは、図2の太線で囲んだ数のように、縦横に隣り合う6つの数の和について調べてみたところ、縦横に隣り合う6つの数の和も、（かけられる数の和）×（かける数の和）となることが分かりました。
図2において、$p+q+r+s+t+u=162$ となるとき、$p$のかけられる数$x$、かける数$y$の値を、それぞれ求めなさい。
解答・解説
問1 ア：[例] 1 イ：[例] 2 ウ：[例] 2 エ：[例] 4 オ：[例] 9
図1より縦横に隣り合う数を書けば良い
問2 ア：[例] $m(n+1)$ イ：[例] $(m+1)n$ ウ：[例] $(m+1) (n+1)$ エ：$m$ オ：$m+1$ カ：$n$ キ：$n+1$
優さんのノートを参考に、かけられる数$m$、かける数$n$をそれぞれ◯と□に当てはめて考えると、ア、イ、ウが求まる。
求めた値から4つの数の和を$m$、$n$を使って表すと因数分解ができ、予想Ⅱの(かけられる数の和)×(かける数の和)が成り立つように式を変形するとエ、オ、カ、キが求まる。
問3 $x=4$、$y=5$
(かけられる数の和)×(かける数の和)が成り立つとき、${x+(x+1)+ (x+2)}×{y+(y+1)+ (y+2)}=162$が成り立つ。この方程式を解けば良い。
0120-740-100
LINE問合せ窓口
LINEからもお問合せいただけます！
公式Instagram
勉強のお役立ち情報を配信中！
お問い合わせ、ご質問も受付中です！
ご質問などお気軽にお問い合わせください。
大問3
問題文
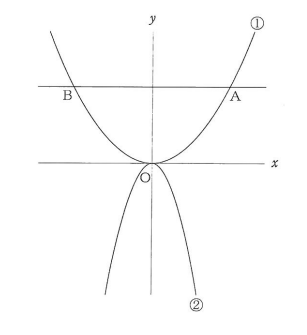
下の図のように、2つの関数 $y=ax^2$ ($a$ は正の定数)……①、$y=-3x^2$ ……② のグラフがあります。①のグラフ上に点Aがあり、点Aの $x$ 座標を正の数とします。点Aを通り、$x$ 軸に平行な直線と①のグラフとの交点をBとします。点Oは原点とします。
次の問いに答えなさい。
問1
$a=2$ とします。点Aの $y$ 座標が $8$ のとき、点Aと点Bとの距離を求めなさい。
問2
①について $x$ の値が $1$ から $3$ まで増加するときの変化の割合が、一次関数 $y=x+2$ について $x$ の値が $-1$ から $2$ まで増加するときの変化の割合に等しいとき、$a$ の値を求めなさい。
問3
$a = \frac{1}{3}$ とします。点Aの $x$ 座標を $3$ とします。②のグラフ上に点Cを、$x$ 座標が $-1$ になるようにとります。点Cを通り、$x$ 軸に平行な直線と②のグラフとの交点をDとします。線分AB, CD上にそれぞれ点P, Qをとり、点Pの $x$ 座標を $t$ とします。ただし $0 < t \le 1$ とします。
陸さんは、コンピュータを使って直線PQを動かしたところ、直線PQが原点Oを通るとき、台形ABDCの面積を2等分することに気づきました。直線PQが原点Oを通るとき、次の（1）、（2）に答えなさい。
（1）点Qの座標を、$t$ を使って表しなさい。
（2）直線PQが台形ABDCの面積を2等分することを説明しなさい。
解答・解説
問1 4
①の式に $a=2, y=8$ を代入すると $x=\pm 2$ となる。これがそれぞれ点 $A$ と点 $B$ の $x$ 座標である。つまり2点間の距離は4。
問2 $a=\frac{1}{4}$
関数 $y=ax^2$ の変化の割合は $\frac{9a-a}{3-1} = 4a$
1次関数 $y=x+2$ の変化の割合は $1$
$4a=1$ より $a=\frac{1}{4}$
問3
（1）$Q(-t, -3)$
直線 $PQ$ は原点を通り点 $P$, 点 $Q$ は原点に対して対称である。点 $P(t, 3)$ から点 $Q$ の座標が求められる。
（2）[解答例]
(台形 $PQCA$ の面積) = ${(3-t)+(t+1)} \times 6 \times \frac{1}{2} = 12$ となる。 ……①
(台形 $ABDC$ の面積) = $(6+2) \times 6 \times \frac{1}{2} = 24$ となる。 ……②
①、②より、
(台形 $PQCA$ の面積) = (台形 $ABDC$ の面積) $\times \frac{1}{2}$ である。
したがって, 直線 $PQ$ は台形 $ABDC$ の面積を2等分する。
(台形の面積) = (上底+下底) $\times$ 高さ $\div 2$ で求められる。
$t$ の関数で示した点 $P$, 点 $Q$ の座標を用いて (台形 $PQCA$ の面積) と (台形 $ABDC$ の面積) をそれぞれ求める。
そこから (台形 $PQCA$ の面積) が (台形 $ABDC$ の面積) の半分であることを確かめる。直線 $PQ$ は台形 $ABDC$ の面積を2等分することが示せた。
大問4
問題文
次の図のように、円Oの円周上に3点A, B, Cをとります。$\angle BAC$ の二等分線と線分BCとの交点をDとします。
次の問いに答えなさい。
問1 $AD=CD$, $\angle BAD=35^{\circ}$ のとき、$\angle ADC$ の大きさを求めなさい。
次の図のように、円Oの円周上に3点A, B, Cをとります。$\angle BAC$ の二等分線と線分BCとの交点をDとします。
次の問いに答えなさい。
問1
$AD=CD$, $\angle BAD=35^{\circ}$ のとき、$\angle ADC$ の大きさを求めなさい。
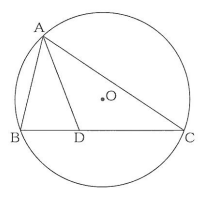
問2 悠斗さんと由美さんは、コンピュータを使って、画面のように、線分ADを延長した直線と円Oとの交点をEとしました。次に、点A, B, Cを円周上で動かし、悠斗さんは「$\triangle ABD$ と $\triangle CED$ が相似である」、由美さんは「$\triangle ABD$ と $\triangle AEC$ が相似である」と予想し、それぞれ予想が成り立つことを証明しました。
問2
悠斗さんと由美さんは、コンピュータを使って、画面のように、線分ADを延長した直線と円Oとの交点をEとしました。
次に、点A, B, Cを円周上で動かし、悠斗さんは「$\triangle ABD$ と $\triangle CED$ が相似である」、由美さんは「$\triangle ABD$ と $\triangle AEC$ が相似である」と予想し、それぞれ予想が成り立つことを証明しました。
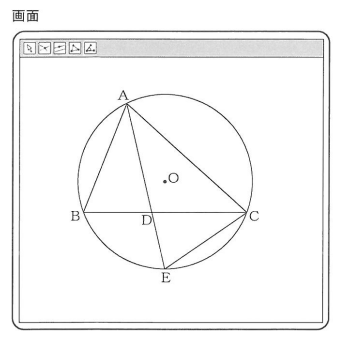
【悠斗さんの証明】
$\triangle ABD$ と $\triangle CED$ において、
【 ア 】に対する【 イ 】は等しいから、
$\angle ABD = \angle CED$ ･･･①
また、対頂角は等しいから、
$\angle ADB = \angle CDE$ ･･･②
①、②から、
【 ウ 】ので、
$\triangle ABD \sim \triangle CED$
【由美さんの証明】
$\triangle ABD$ と $\triangle AEC$ において、
【 ア 】に対する【 イ 】は等しいから、
$\angle ABD = \angle AEC$ ･･･①
また、仮定から、
$\angle BAD = \angle EAC$ ･･･②
①、②から、
【 ウ 】ので、
$\triangle ABD \sim \triangle AEC$
次の（1）、（2）に答えなさい。
（1）【 ア 】～【 ウ 】には、それぞれ共通する言葉が入ります。【 ア 】～【 ウ 】に当てはまる言葉をそれぞれ書き入れ、照明を完成させなさい。
（2）$AB=AD$ のとき、$\triangle ABE \equiv \triangle ADC$ を証明しなさい。なお、悠斗さんや由美さんが証明したことを用いてもよいものとします。
解答・解説
問1 $110^{\circ}$
角の二等分線の性質から $\angle CAD=15^{\circ}$ になる。$\triangle ADC$ は二等辺三角形なので $\angle ADC=110^{\circ}$。
問2
（1）ア：[例] 弧 $AC$ イ：円周角 ウ：[例] 2組の角がそれぞれ等しい
ア、イは円周角の定理についてである。また、仮定から導ける三角形の相似条件をウに書けば良い。
（2）[解答例①]
$\triangle ABE$ と $\triangle ADC$ において、
仮定より、$AB=AD$ ……①
また、仮定より、$\angle BAE=\angle DAC$ ……②
弧 $AB$ に対する円周角は等しいので、
$\angle BEA=\angle DCA$ ……ア
$\angle ABE=180^{\circ}-(\angle BEA+\angle BAE)$ ……イ
$\angle ADC=180^{\circ}-(\angle DCA+\angle DAC)$ ……ウ
②、ア、イ、ウより、$\angle ABE=\angle ADC$ ……③
①、②、③より、1組の辺とその両端の角がそれぞれ等しいので、$\triangle ABE \equiv \triangle ADC$
[解答例②]
(①までは解答例①と同様とする。)
また、仮定より、$\angle BAE=\angle DAC$ ……②
$\triangle ABD \sim \triangle AEC$ から、対応する辺の比は等しいので、$AB:AD=AE:AC=1:1$
よって、$AE=AC$ ……③
①、②、③より、2組の辺とその間の角がそれぞれ等しいので、$\triangle ABE \equiv \triangle ADC$
[解答例③]
(①までは解答例①と同様とする。)
$\triangle ABD \sim \triangle AEC$ から、対応する辺の比は等しいので、$AB:AD=AE:AC=1:1$
よって、$AE=AC$ ……②
$\triangle ABD \sim \triangle CED$ から、対応する辺の比は等しいので、$AB:AD=CE:CD=1:1$
よって…$CD=CE$ ……ア
仮定より、$\angle BAE=\angle EAC$ であるから、弧 $BE$ と 弧 $CE$ の長さが等しいので、$\angle BCE=\angle EBC$
底角が等しいので、$\triangle BEC$ は、$BE=CE$ の二等辺三角形である。 ……イ
ア、イより、$BE=DC$ ……③
①、②、③より、3組の辺がそれぞれ等しいので、$\triangle ABE \equiv \triangle ADC$
正答例は多数存在するが、合同を示す三角形 $\triangle ABE \equiv \triangle ADC$、円周角の定理や相似の図形の性質を用いて仮定を書き、それに対応する三角形の合同条件などを書く必要がある。
LINE問合せ窓口
LINEからもお問合せいただけます！
公式Instagram
勉強のお役立ち情報を配信中！
お問い合わせ、ご質問も受付中です！
ご質問などお気軽にお問い合わせください。
大問5
問題文
A氏に住む中学生の翼さんは、ニュースで聞いたことをもとに、先生と話し合っています。
翼さん：「昨日、ニュースで『今年の夏は暑くなりそうだ』と言っていましたよ。」
先生 ：「先生が子どもだった50年くらい前は、もっと涼しかったんですけどね。」
翼さん：「どのくらい涼しかったんですか？」
先生 ：「最高気温が25℃以上の『夏日』は、最近よりずっと少なかったはずです。」
翼さん：「そうなんですか。家に帰ったら調べてみますね。」
次の問いに答えなさい。
問1
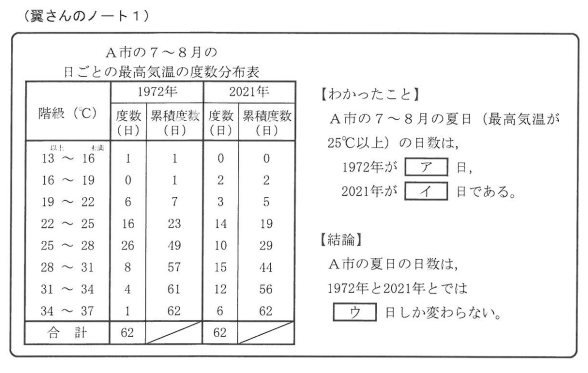
翼さんは、今から50年前と2021年の夏日の日数を比べてみることにしました。翼さんは、A市の1972年と2021年における、7月と8月の日ごとの最高気温を調べ、その結果をノートにまとめました。次の【 ア 】～【 ウ 】に当てはまる数を、それぞれ書きなさい。
問2
翼さんは、ノートを見せながら、先生と話し合っています。
翼さん：「A市の夏日の日数は、50年前とほとんど変わりませんでした。」
先生 ：「本当ですか。ん？7月と8月以外の月でも真夏になることがありますよ。それに、調べた1972年と2021年の夏日の日数が、たまたま多かった、あるいは、たまたま少なかったという可能性もありますよね。」
翼さん：「確かにそうですね。もう少し調べてみます！」
翼さんは、A市の夏日の年間日数について、1962年から1981年までの20年間（以下、「X期間」とします。）と、2012年から2021年までの10年間（以下、「Y期間」とします。）をそれぞれ調べ、その結果をノートにまとめることにしました。
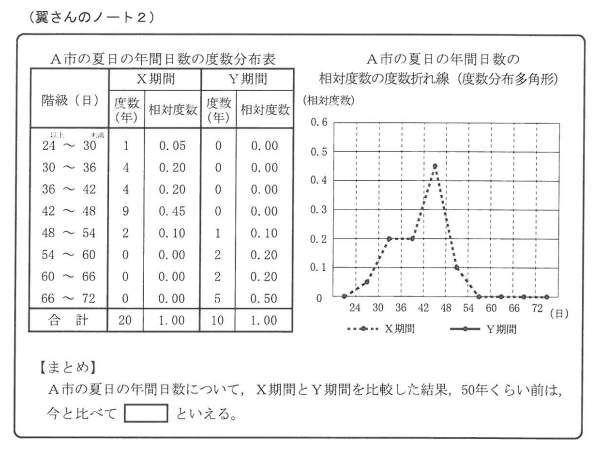
次の(1)～(3)に答えなさい。
（1）ノート2の度数分布表をもとに、Y期間の相対度数の度数折れ線（度数分布多角形）を、解答用紙にかき入れなさい。
（2）ノート2において、翼さんが「度数」ではなく「相対度数」をもとに比較している理由を説明しなさい。
（3）に当てはまる言葉として最も適当なものを, 次のア～ウから選びなさい。 また、選んだ理由を、X期間とY期間の2つの相対度数の度数折れ線（度数分布多角形）の特徴と、その特徴から読み取れる傾向をもとに説明しなさい。
ア 暑かった
イ 変わらなかった
ウ 涼しかった
解答・解説
問1 ア：39 イ：43 ウ：4
日毎の最高気温の度数分布からア、イの数値を読み取り、その差がウになる。
問2
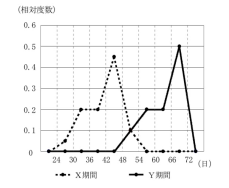
（1）図を参照
$Y$期間の表を見ながらグラフをプロットする。
（2）[解答例] $X$ 期間と $Y$ 期間では、度数の合計が異なるから。
（3）記号：ウ
説明：[解答例] つの度数折れ線が同じ様な形をしていて, $X$ 期間の方が $Y$ 期間よりも左側にあり(①)、$X$ 期間は、$Y$ 期間より夏日の年間日数が少ない傾向にあると言えるから(②)
①は $X$ 期間の方が $Y$ 期間よりも左側にあることが書かれていれば良い。②は $X$ 期間が、$Y$ 期間より夏日の年間日数が少ないことが書かれていれば良い。
志望校に合わせた受験対策なら、やる気アシストにお任せ下さい！
家庭教師のやる気アシストは、北海道にお住まいの受験生のお子さんを毎年たくさん指導をさせ頂き、合格に導いています。
高い合格率の秘訣は、指導経験豊富な先生の指導力に加え、1対1の指導でお子さん一人ひとりの状況に合わせた、お子さんだけのカリキュラムで勉強が進められるから！
家庭教師のやる気アシストは、お子さんの志望校合格まで全力でサポートさせて頂きます！
LINE問合せ窓口
LINEからもお問合せいただけます！
公式Instagram
勉強のお役立ち情報を配信中！
お問い合わせ、ご質問も受付中です！
ご質問などお気軽にお問い合わせください。
アシストの指導方法がじっくり見れる！知れる！無料の体験授業実施中
お子さんにとって「成果が出る勉強法」ってどんな勉強法だと思いますか？
お子さんそれぞれに、個性や性格、学力の差もあります。そんな十人十色のお子さん全員に合う勉強法ってなかなかないんです。
たからこそ、受験生の今だけでもお子さんだけの勉強法で受験を乗り越えてみませんか？
やる気アシストには、決まったカリキュラムはありません。お子さんの希望や学力、得意や不得意に合わせて、お子さんだけのカリキュラムで指導を行っていきます。また、勉強法もお子さんそれぞれに合う合わないがあります。無料体験授業では、お子さんの性格や生活スタイルを見せていただき、お子さんにとって効率的な成果の出る勉強のやり方をご提案させて頂きます。
