







京都府の2021年3月実施の令和3年度(2021年度)入学者の公立高校入試問題の解説をしています。
受験勉強において、過去問を解くことはとても効果的な勉強法です。ぜひ、受験までに一度挑戦し、問題の傾向を掴んでおきましょう。合わせて、対策などをたてられるととても良いですね。
また、過去問で苦手な点が見つかった場合は、そこを中心に試験日当日までにしっかりと対策しておきましょう。
今年の京都府の数学の前期試験の難易度は標準です。
大問が6つ構成で、図形問題の比重が大きく難易度も高いです。
小問集合と各大問の最初の問題は簡単なのでここを必ず押さえると得点が稼げます。
また、大問2の確率と、大問6の法則性を問う問題は丁寧に解いていくと答えを出せるので次に点数が取りやすい部分です。
中期試験の難易度は難です。
考えさせる問題が多く、取っ掛かりを見つけないと完全解答まで難しい問題が出題されます。
ただ、同じく小問集合や各大問の最初の問題は比較的簡単なので押さえていきましょう。
解けなかった問題も出来るまで解く復習用の問題として使えるほど骨のある問題です。
【京都府】令和3年度一般入学者選抜の過去問はこちらから
数学(中期)の過去問題はこちら>>
次の問い(1)~(8)に答えよ。
(1) (-4)²ー9÷-3を計算せよ。
(2) 6x²y×2y÷9÷8xy²を計算せよ。
(3) 1/√8×4√6ー√27を計算せよ。
(4) x=1/5, y=-3/4のとき、(7xー3y)ー(2x+5y)の値を求めよ。
(5) 二次方程式(x+1)²=72を解け。
(6) 関数y=1/2x²についてxの値が2から6まで増加するときの変化の割合を求めよ。
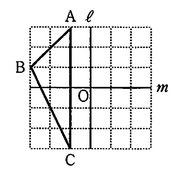
(7) 右の図のように、方眼紙上に△ABCと2直線ℓ、mがある。3点A,B,Cは方眼紙の縦線と横線の交点上にあり、直線ℓは方眼紙の縦線と、直線mは方眼紙の横線とそれぞれ重なっている。2直線ℓ、mの交点をOとするとき、△ABCを点Oを中心として点対称移動させた図形を答案用紙の方眼紙上にかけ。
(8)4枚の硬貨を同時に投げるとき、表が3枚以上出る確率を求めよ。ただし、それぞれの効果の表裏の出方は、同様に確からしいものとする。
(1) 【正答 19】
(与式)=16+3=19
(2) 【正答 x/6】
(与式)=12x²y²/(72xy²)=x/6
(3) 【正答 -√3】
(与式)=4√6/2√2-3√3=2√3-3√3=√3
(4) 【正答 7】
(7x-3y)-(2x+5y)=5x-8y
x=1/5, y=-3/4 を代入すると
1+6=7
(5) 【正答 -1±6√2】
与式よりx+1=±√72
∴x=-1±6√2
(6) 【正答 -4】
変化の割合は(yの増加量)/(xの増加量)で定義されるから、求める変化の割合は
(-1/26^2+1/22^2)/(6-2)=(-18+2)/4=-4
(7) 【正答】
(8) 【正答 5/16】
それぞれの硬貨について表と裏の2通りの出方があるので、4枚同時に投げた時の場合の数は
2x2x2x2=16通り。そのうち、3枚以上表になっているのは、コイン4枚をA,B,C,Dと区別すると、Aだけ裏の時、Bだけ裏の時、Cだけ裏の時、Dだけ裏の時と4枚すべてが表になっているときの5通りなので求める確率は5/16
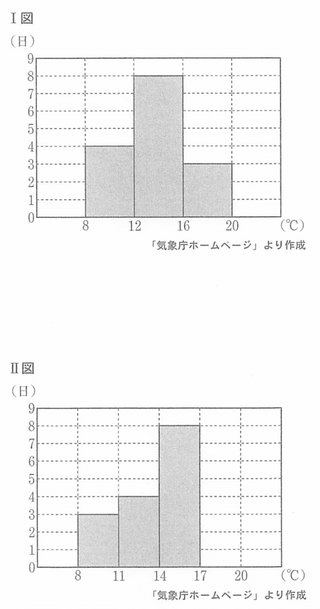
Ⅰ図は、2019年3月1日から15日間の一日ごとの京都市の最高気温について調べ、その結果をヒストグラムに表したものである。たとえば、Ⅰ図から、2019年3月1日からの15日間のうち、京都市の最高気温が8℃以上12℃未満の日は4日あったことがわかる。このとき、次の問い(1)・(2)に答えよ。
(1)Ⅰ図において、それぞれの階級にはいっている資料の個々の値が、どの値もすべてその階級の階級値であると考えて、1日ごとの京都市の最高気温の、2019年3月1日から15日間の平均値を、小数第2位を四捨五入して求めよ。
(2)Ⅱ図は、2019年3月1日から15日間の一日ごとの京都市の最高気温について、Ⅰ図とは階級の幅を変えて表したヒストグラムである。Ⅰ図とⅡ図から考えて、2019年3月1日からの15日間のうち、京都市の最高気温が14℃以上16℃未満の日は何日あったか求めよ。
(1) 【正答 13.7】
8℃以上12℃未満の日は4日
12℃以上16℃未満の日は8日
16℃以上20℃未満の日は3日
それぞれ階級値は10℃,14℃,18℃であるから平均値は
(10×4+14×8+18×3)/15=13.73…
小数第2位を四捨五入して13.7を解答とする。
(2) 【正答 5】
図IIより14℃以上の日は8日あったことがわかる。また、図Iより16℃以上の日は3日あったことがわかる。これらより14℃以上16℃未満の日は5日あったことがわかる。
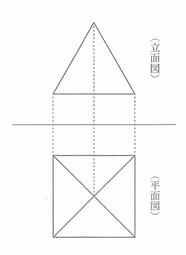
図のような、正三角錐の投影図がある。この投影図において、立面図は1辺が6㎝、高さが3√3㎝の正三角形である。
このとき、次の問い(1)・(2)に答えよ。
(1)正四角錐の体積を求めよ。
(2)正四角錐の表面積を求めよ。
(1) 【正答 36√3】
正四角錐の底面積は36㎠.高さは3√3より求める体積VはV=36×3√3×1/3=36√3
(2) 【正答 108】
表面積は底面と側面4つの和で求められる。
側面の三角形は底辺6cm, 高さ6cmの三角形である。(図に示されているのは投影図であるから側面は1辺が6cmの正三角形ではないことに注意)
以上より求める表面積SはS=6×6+(6×6/2)×4=108
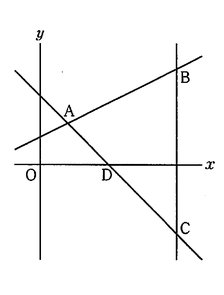
図のように、直線y=1/2x+2と直線y=-x+5が点Aで交わっている。直線y=1/2x+2上にx座標が10である点Bをとり、点Bを通りy軸と平行な直線と直線y=-x+5との交点をCとする。また、直線y=-x+5とx軸との交点をDとする。
このとき、次の問い(1)・(2)に答えよ。
(1)2点B,C間の距離を求めよ、また点Aと直線BCとの距離を求めよ。
(2)点Dを通り△ABCの面積を2等分する直線の式を求めよ。
(1) 【正答 12,8】
点Bのx座標は10であるからy=1/2x+2に代入してB(10, 7) 同様にしてC(10, -5)であるから二点間の距離は12。
点Aは二つの直線の交点であるからy=1/2x+2, y=-x+5の連立方程式を解く。
A(2, 3)であり、x座標の差が距離と等しくなるから求める距離は8。
(2) 【正答 23x/25-23/5】
△ABCの面積Sは、BCの長さを底辺とし、点AとBC間の長さを高さとすれば求められるので、S=12*8/2=48
求める直線が通るBC上の点をEとする。△DCEの面積が24となればよいことからEのy座標を求める。
DはD(5, 0)であるからECの長さは48/5。
Eのy座標は23/5
D(5, 0)とE(10, 23/5)を通る直線が求める直線の式である。
図のように、円Oの周を3等分する点A,B,Cがある。線分OB上に点を、OD:DB=5:8となるようにとる。また、円の周上に点Eを、線分CEが円Oの直径となるようにとる。点Eを含むおうぎ形OABの面積は54π㎠である。
このとき、次の問い(1)~(3)に答えよ。
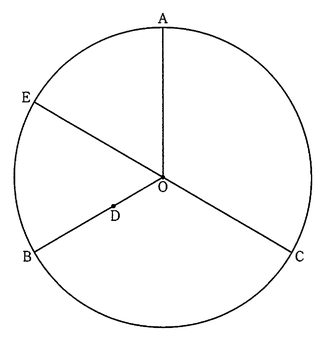
(1)点を含むおうぎ形OABの中心角の大きさを求めよ。
(2)円Oの半径を求めよ。
(3)線分ADと線分CEとの交点をFとするとき、線分CFの長さを求めよ。
(1) 【正答 120°】
A,B,Cは円周を三等分しているので、360/3=120
(2) 【正答 9√2】
扇形の面積SはS=rrπ*a/360 (r:半径、a:中心角)であるから
54π=r²*120/360
r²=162π
r=9√2π
(3) 【正答 23√2/2】
錯角より∠DOF=∠AEF
対頂角より∠OFD=∠EFA
よって△ODF∽△EAFである。
また、OA=OE、∠AOE=60°より△AOEは正三角形であるからAE=OB。
△ODFと△EAFの相似比は5:13であるからCFの長さは9√2+9√2*(5/18)=23√2/2
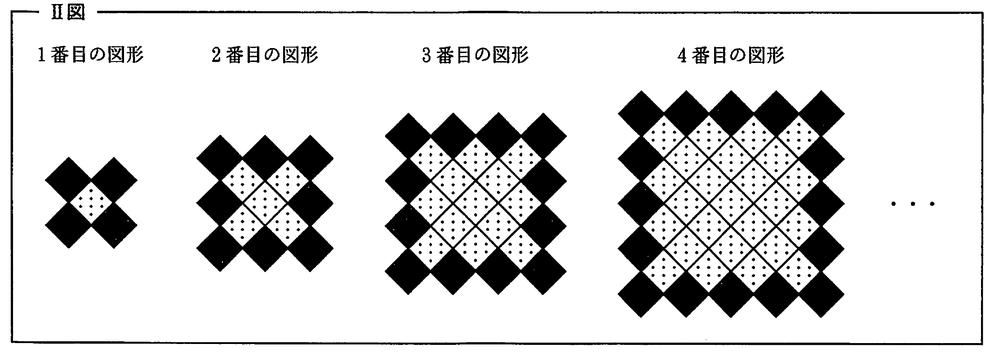
Ⅰ図のような、タイルAとタイルBが、それぞれたくさんある。タイルAとタイルBを、次のⅡ図のように、すき間なく規則的に並べたものを、1番目の図形、2番目の図形、3番目の図形、…とする。
たとえば、2番目の図形において、タイルAは8枚、タイルBは5枚である。
このとき、次の問い(1)~(3)に答えよ。
(1)5番目の図形についてタイルAの枚数を求めよ。
(2)9番目の図形についてタイルBの枚数を求めよ。
(3)タイルAの枚数がタイルBの枚数より1009枚少なくなるのは何番目の図形か求めよ。
(1) 【正答 20】
四角形の各辺に1枚ずつ足されている、と考えられるのでn番目からn+1番目になると4枚足されるので5番目は20枚
(2) 【正答 145】
1番目から1, 5, 13, 25, …と増えておりまたその差は4, 8, 12, …と増えている。
このことよりn番目の図形のタイルBの枚数は2n^2-2n+1で表されるので9番目のタイルは145枚
(3) 【正答 24】
タイルAは4n, タイルBは2n^2-2n+1で表されるのでその差は2n^2-6n+1でこれが1009となる等式を解けば良い。
2n²-6n+1=1009
2n²-6n=1008
n²-3n=504
(n-24)(n+21)=0
n>0よりn=24
家庭教師のやる気アシストは、京都府にお住まいの受験生のお子さんを毎年たくさん指導をさせ頂き、合格に導いています。
おかげさまで、昨年度の合格率は、関西エリア全体で97.3%という結果を残すことが出来ました。
高い合格率の秘訣は、指導経験豊富な先生の指導力に加え、1対1の指導でお子さん一人ひとりの状況に合わせた、お子さんだけのカリキュラムで勉強が進められるから!
家庭教師のやる気アシストは、お子さんの志望校合格まで全力でサポートさせて頂きます!
お子さんにとって「成果が出る勉強法」ってどんな勉強法だと思いますか?
お子さんそれぞれに、個性や性格、学力の差もあります。そんな十人十色のお子さん全員に合う勉強法ってなかなかないんです。
たからこそ、受験生の今だけでもお子さんだけの勉強法で受験を乗り越えてみませんか?
やる気アシストには、決まったカリキュラムはありません。お子さんの希望や学力、得意や不得意に合わせて、お子さんだけのカリキュラムで指導を行っていきます。また、勉強法もお子さんそれぞれに合う合わないがあります。無料体験授業では、お子さんの性格や生活スタイルを見せていただき、お子さんにとって効率的な成果の出る勉強のやり方をご提案させて頂きます。

