【京都府】令和4年度/2022年度入学者高校入試選抜試験：数学の解説
京都府の2022年3月実施の令和4年度（2022年度）入学者の公立高校入試問題の解説をしています。
受験勉強において、過去問を解くことはとても効果的な勉強法です。ぜひ、受験までに一度挑戦し、問題の傾向を掴んでおきましょう。合わせて、対策などをたてられるととても良いですね。
また、過去問で苦手な点が見つかった場合は、そこを中心に試験日当日までにしっかりと対策しておきましょう。
今年の京都府の数学の前期試験の難易度は標準です。
大問が6つ構成で、図形問題の比重が大きく難易度も高いです。
小問集合と各大問の最初の問題は簡単なのでここを必ず押さえると得点が稼げます。
また、大問2の確率と、大問6の法則性を問う問題は丁寧に解いていくと答えを出せるので次に点数が取りやすい部分です。
中期試験の難易度は難です。
考えさせる問題が多く、取っ掛かりを見つけないと完全解答まで難しい問題が出題されます。
ただ、同じく小問集合や各大問の最初の問題は比較的簡単なので押さえていきましょう。
解けなかった問題も出来るまで解く復習用の問題として使えるほど骨のある問題です。
【京都府】令和4年度一般入学者選抜の過去問はこちらから
【前期】大問1
問題文
次の問い（1）～（9）に答えよ。
（1） (-5)²ー2³÷4 を計算せよ。
（2） 3ab/2÷ab²/6×(-a²b) を計算せよ。
（3） √6×√18－9/√27 を計算せよ。
（4） 次の連立方程式を解け。
3x－(y+8)＝12
x－2y＝0
（5) 1次関数 y=-7x/3+5 について、xの増加量が6のときのyの増加量を求めよ。
（6） (x-y)²-49 を因数分解せよ。
（7） 2次方程式 4x²-4x-1=0 を解け。
(8) 底面の半径が3㎝、母線の長さが5㎝である円錐を2つ用意し、2つの円錐の底面をぴったりと重ねると、次のような立体ができた。このとき、できた立体の表面積を求めよ。
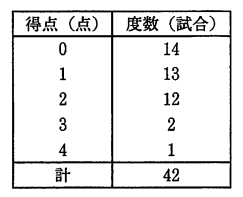
(9) 右の表は、あるサッカーチームが1年間に行ったそれぞれの試合の得点を調べ、その結果を度数分布表に整理したものである。
このとき、次の(ア)～(ウ)を、値の小さいものから順に並べ替え、記号で書け。
(ア) 得点の平均値 (イ) 得点の中央値 (ウ) 得点の最頻値
解答・解説
（1） 【正答 23】
加減乗除は乗除から計算する
【与式】＝25ー8÷4＝25ー2＝23
（2） 【正答 -9a²】
（3） 【正答 5√3】
【与式】＝√6×√18－9/√27＝6√3－√3
＝5√3
（4） 【正答 (x＝)8、(y＝)4 】
3x－(y+8)＝12 ー①
x－2y＝0 ー②
②を変形して
x＝2y これを①に代入する
3×(2y)－(y+8)＝12
⇔y＝4
x＝8
（5） 【正答 -14】
(傾き)＝(yの増加量)/(xの増加量)なので
⇔-7/3＝(yの増加量)/6
⇔(yの増加量)＝-14
（6） 【正答 (x-y+7)(x-y-7)】
【与式】＝(x-y)²-7²＝{(x-y)+7}{(x-y)-7}
＝(x-y+7)(x-y-7)
（7） 【正答 (1±√2)/2】
2次方程式の解の公式を使う
x＝（2±√4−4×(-1)）/4
＝(1±√2)/2
（8） 【正答 30π ㎠】
円錐の側面の表面積は
(母線)×(母線)×(半径)/(母線)×π
＝(母線)×(半径)×π
＝5×3×π
これが2つあるので
15π×2＝30π
（9） 【正答 ウ→イ→ア】
(ア) 得点の平均値は (0×14+1×13+2×12+3×2+4×1)/42=1.11…
(イ) 得点の中央値は１
(ウ) 得点の最頻値は０
大問２
問題文
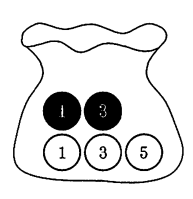
２ 図のように、1、3の数が書かれた黒玉と1、3、5の数が書かれた白玉がそれぞれ1個ずつ、合計5個の玉が入っている袋がある。
このとき、次の問い（1）、（2）に答えよ。ただし、袋に入っているどの玉が取り出されることも同様に確からしいものとする。
（1）5個の玉が入っている袋から玉を1個取り出し、取り出した玉に書かれている数を調べてから袋にもどす。次に、もう一度この袋から玉を1個取り出し、取り出した玉に書かれている数を調べる。このとき、はじめに取り出した玉に書かれている数と、次に取り出した玉に書かれている数が等しくなる確率を求めよ。
（2）5個の玉が入っている袋から玉を同時に2個取り出し、取り出した2個の玉のうち、白玉の個数をa個とする。また、取り出した2個の玉に書かれている数の和をbとする。このとき、4a=bとなる確率を求めよ。
解答・解説
（1） 【正答 9/25】
1回目に1を取り出す確率は2/5
2回目に続けて1を取り出す確率は2/5
より、1を連続で引く確率は
2/5×2/5=4/25
3を連続で取り出す確率も同様に考えて、4/25
5を連続で取り出す確率は
1/5×1/5=1/25
よって
4/25+4/25+1/5=9/25
（2） 【正答 3/10】
5個の玉から2個を引くので、組み合わせ方は全部で₅Ｃ₂=10通りとなる
a=1のときb=4の場合、
取り出し方は、①と❸、❶と③の2通り
a=2のときb=8の場合、
取り出し方は、➄と③の1通り
よって求める確率は、3/10
大問３
問題文
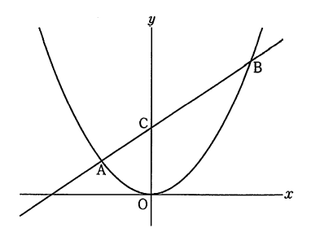
３ 右の図のように、関数 y=ax² のグラフ上に2点A、Bがあり、点Aの座標は(-3，2)、点BのXx座標は6である。また、2点A、Bを通る直線とy軸との交点をCとする。
このとき、次の問い（1）～（3）に答えよ。
（1）aの値を求めよ。
（2）直線ABの式を求めよ。
（3）x軸上に点Dを、線分BDと線分CDの長さの和が最も小さくなるようにとるとき、△BCDの面積を求めよ。
解答・解説
（1） 【正答 (a=) 2/9 】
y=ax² に(-3，2)を代入すると
2=a(-3)²
⇔a= 2/9
（2） 【正答 (y=) 2x/3+4】
Bの座標は y=2x²/9 にx=6を代入
y=2×6²/9=8
A(-3，2)、B(6，8)ー①より
傾きは(2-8)/(-3-6)=2/3
y=2x/3+b に(-3，2)を代入
2=2×(-3)/3+b
⇔b=4
よって y=2x/3+4
（3） 【正答 16】
点Cをx軸について線対象に移動させた点をC’とする
線分BC’とx軸が交わる点にDがあるとき、線分BDと線分CDの長さの和が最も小さくなる
このとき、BD+CD=BD+C’D となる
点Cは、y=2x/3+4とy軸の交点なので
x=0、y=0+4=4
C(0，4) ー②
②より点C'(0，-4) ー③
①と③より
直線BC’の傾きは(-4-8)/(0-6)=2
y=2x+b に(0，-4)を代入
-4=0+b
⇔b=-4
よって y=2x-4 ー④
点Dの座標は④から D(2，0)
△BCD=△BCC’-CC’D=8×6×1/2－8×2×1/2
=16
大問４
問題文
４ 図のように、正三角形ABCがあり、辺BC上に点Dを、BD：DC＝7：2となるようにとる。また、△ABCと同じ平面上に点Eを、△ADEが正三角形となるようにとる。
このとき、次の問い（1）、（2）に答えよ。ただし、点Eは直線ADに対して点Bと同じ側にないものとする。
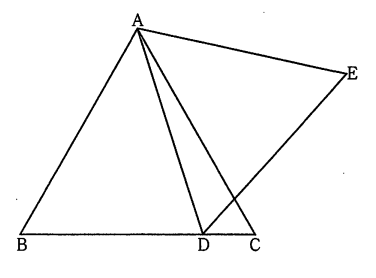
（1）△ABD≡△ACEであることを証明せよ。
（2）2点C、Eを通る直線と直線ADとの交点をFとするとき、EC：CFを最も簡単な整数の比で表せ。
解答・解説
（1） 【正答 (例) 】
△ABDと△ACEで
△ABCは正三角形だから、 AB=AC ー①
△ADEは正三角形だから、 AD=AE ー②
∠BAC=60°だから ∠BAD=60°－∠CAD
∠DAE=60°だから ∠CAE=60°－∠CAD
よって、 ∠BAD=∠CAE ー③
①、②、③から、2組の辺とその間の角が、それぞれ等しいので
△ABD≡△ACE
（2） 【正答 EC：CF＝49：18】
△ABD、△FCDにおいて
対頂角は等しいので ∠ADB=∠FDC ー①
△ABD≡△ACEから ∠ABD=∠ACE=60° ー②
△ABCは正三角形だから、 ∠ACB=60° ー③
②、③より ∠DCF=180°－∠ACE－∠ACB=60° ー④
④より ∠DBA=∠DCF=60° ー➄
①、➄より2つの角が等しいので
△ABD∽△FCD ー⑥
BD：CD=7：2
⑥より
AB：FC=7⃣：2⃣
また、△ABCは正三角形なので
AB=BC=7⃣=9 ー⑦
(1)からAD=CE=7 ー⑧
よって、⑦、⑧より
EC：CF＝7：2⃣=7：2⃣×9/7⃣=7：18/7
=49：18
大問５
問題文
５ 右の図のように、直方体ABCD-EFGHがあり、AB＝AD＝4㎝、AE＝2√3㎝である。また、2辺EF、EHの中点をそれぞれI、Jとする。
このとき、次の問い（1）～（3）に答えよ。
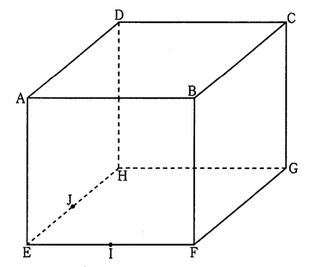
（1）線分IJの長さを求めよ。
（2）四角形BDJIの面積を求めよ。
（3）2点A、Gを通る直線と四角形BDJIとの交点をKとするとき、四角錘KEFGHの体積を求めよ。
解答・解説
（1） 【正答 2√2 】
△IEJに注目すると、1：1：√2の三角形になっているので、IJ＝2√2ｃｍ
（2） 【正答 6√7 】
IJと同様にして、DB,DJ,BIを求めると、それぞれ4√2ｃｍ、4ｃｍ、4ｃｍとなる。ここで四角形ＢＤＪＩを書いてみると台形の形になることが分かる。この台形を3分割して面積を求めればよい。
√2×√14÷2×2+2√2×√14＝6√7ｃｍ²
（3） 【正答 32√3/5】
点Ｋは四角形ＢＤＪＩの真ん中になるので、ＢＤの中点をＭ、ＩＪの中点をＮとすると、ＡＭ－Ｋ－ＧＮで砂時計の形が作れることが分かる。
四角錐ＫＥＦＧＨの体積は1/3×底面積（四角形ＥＦＧＨ）×高さ（ＫＧ）で求めることができる。
底面積は4×4＝16ｃｍ²
ＫＧを求めるためにはＡＭ－Ｋ－ＧＮの砂時計の形に注目する。
ＡＭ＝2√2、ＮＧ＝3√2となるので、△ＡＭＫと△ＧＮＫは2：3の相似である。よって、ＫＧ＝3/5×ＡＧ＝3/5×2√3
答えは、32√3/5ｃｍ³となる。
大問６
問題文
６ 右の図のような、長いすAと長いすBが、それぞれたくさんある。長いすAには1脚あたり必ず2人座り、長いすBには1脚あたり必ず3人座るものとする。長いすA、Bを使用してちょうどn人座るとき、長いすA、Bの組み合わせの総数は何通りあるか、長いすAだけを使用する場合と長いすBだけを使用する場合を含めて考える。
たとえば、n＝9人のとき、長いすAを3脚と長いすBを1脚使用する場合と、長いすBだけを3脚使用する場合があるから、長いすA、Bの脚数の組み合わせの総数は2通りである。
次の表は、n＝2、3、4、5、6のときの、長いすA、Bの脚数の組み合わせと、長いすA、Bの脚数の組み合わせの総数をまとめたものである。
このとき、次の問い（1）～（3）に答えよ。ただし、nは2以上の自然数とする。
（1）n＝20のとき、長いすA、Bの脚数の組み合わせの総数は何通りあるか求めよ。
（2）n＝127のとき、長いすA、Bの脚数の組み合わせの総数は何通りあるか求めよ。
（3）aを2以上の自然数とする。長いすA、Bの脚数の組み合わせの総数がa通りあるときのnの値として考えられるもののうち、最小の値と最大の値を、それぞれaを用いて表せ。ただし、答えは、かっこがあればかっこをはずし、同類項があれば同類項をまとめて簡単にすること。
解答・解説
（1） 【正答 4 通り 】
（A,B）＝（10，0）（7，2）（4，4）（1，6）の4通りになります。
（2） 【正答 21通り】
ｎが奇数なので、これを起点に考えると、Ｂは1から41の奇数の21通りとなる。
（3） 【正答 (最小の値) 6a-6 (最大の値) 6a+1】
最小：2×3×（a-1）＝6a-6
最大：2×（3×（a-1）+2）+3＝6a+1
【中期】大問1
問題文
次の問い（1）～（8）に答えよ。
（1） (-3)²ー6×5を計算せよ。
（2） (8a+9)/4ー(6a+4)/3を計算せよ。
（3） (√2+√5)²を計算せよ。
（4） 方程式 0.16xー0.08＝0.4 を解け。
（5） 次の連立方程式を解け。
7x－3y＝11
3x－2y＝-1
（6） 関数y=x²/4についてxの変域がa≦x≦3のときのyの変域がb≦y≦9である。このとき、a、bの値をそれぞれ求めよ。
（7） 次の図で、4点A、B、C、Dは円Oの周上にある。このとき、∠xの大きさを求めよ。
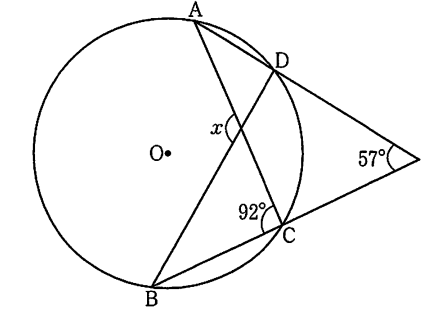
（8） 箱の中に同じ大きさの白玉がたくさん入っている。この箱の中に、同じ大きさの黒玉を50個いれてよくかき混ぜた後、この箱の中から40個の玉を無作為に抽出すると、その中に黒玉が3個含まれていた。この結果から、始めたにこの箱の中に入っていた白玉の個数はおよそ何個と考えられるか。一の位を四捨五入して答えよ。
解答・解説
（1） 【正答 -39】
加減乗除は乗除から計算する
【与式】＝-9-30＝-39
（2） 【正答 11/12】
分母をそろえて計算する
【与式】＝(24a+27)/12－(24a+16)/12＝11/12
（3） 【正答 7+2√10】
展開して計算すればよい
【与式】＝2+2×√10+5＝7+2√10
（4） 【正答 (x＝)3】
0.16xー0.08＝0.4
⇔0.16x＝0.4+0.08＝0.48
⇔x＝3
（5） 【正答 (x＝)5、(y＝)8】
7x－3y＝11 ー①
3x－2y＝-1 ー②
①×2－②×3より
5x＝25⇔ x＝5
これを①の式に代入して、
7×5－3y＝11⇔y＝8
（6） 【正答 (a＝)-6、(b＝)0】
y=x²/4にx＝3を代入して、y＝9/4
y=x²/4にy＝9を代入して、x＝36
x＝36になるxは-6、6
a≦x≦3より、x＝-6（⇔a＝-6）
-6≦x≦3のとき、y=x²/4の最小値は0となるので、
b＝0
（7） 【正答 127°】
直線ADと直線BCの交点を点Eとおく
円周角は等しいので、
∠ADB＝∠ACB＝92°
また
∠ACE＝180°－∠ACB＝180°－92°＝88°
△ACEにおいて
∠EAC＝180°－∠ACE－∠CEA
＝180°－88°－57°＝35°
よって、
∠x＝∠EAC+∠ADB＝35°+92°＝127°
（8） 【正答 およそ620個】
黒玉が40個中3個の割合で含まれているので、
黒玉と白玉がの比は、箱の中の白玉がx個あったとすると
3：40-3＝40：x ⇔ x＝37×50/3＝616.…
1の位を四捨五入するので、x＝620
大問2
問題文
1から6までの目があるさいころを2回投げ、1回目に出た目の数をa、2回目に出た目の数をbとする。
このとき、次の問い(1)・(2)に答えよ。ただし、さいころの1から6までの目の出方は、同様に確からしいものとする。
（1） a/b＝2となる確率を求めよ。
（2） a/bの値が循環小数になる確率を求めよ。
解答・解説
（1） 【正答 1/12】
a/b＝2となるa、bの組み合わせは
(a,b)＝(2,1)、(4,2)、(6,3)
の3通り。すべての組み合わせ方は、6×6＝36通りあるので、
3/36＝1/12
（2） 【正答 2/9】
a/bが循環小数となるa、bの組み合わせは
(a,b)＝(1,3)、(1,6)、(2,3)、(2,6)、(4,3)、(4,6)、(5,3)、(5,6)
の8通り。
8/36＝2/9
大問3
問題文
右の図のように、三角柱ABCーDEFがあり、AB＝8㎝、BC＝4㎝、AC＝AD、∠ABC＝90°である。
このとき、次の問い(1)・(2)に答えよ。
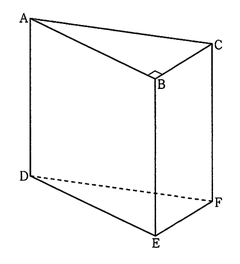
（1）次の文は、点Bと平面ADFCとの距離について述べたものである。文中の▭に当てはまるものを、下の(ア)～(カ)から1つ選べ。
（ア）辺ACの中点
（イ）辺CFの中点
（ウ）線分AFと線分CDとの交点
（エ）∠CBEの二等辺分線と辺CFとの交点
（オ）点Bから辺ACにひいた垂線と辺ACとの交点
（2）2点H、Iをそれぞれ辺AC、DF上にCH＝DI＝9/2㎝となるようにとるとき、四角錘BCHDIの体積を求めよ。
解答・解説
（1） 【正答 (オ)】
点Bと辺ACの距離、点Bと平面ADFCの距離は等しい
（2） 【正答 48】
△ABCについて、三平方の定理より、
AC＝√{(AB²)∔(BC)²}＝∠√(8²∔4²)＝4√5
点Ｂと平面CDHIの距離は、線分BGの長さと等しくなる
△ABCにおいて、線分BCを底辺として面積を求めると
4×8×1/2＝16ー①
また、線分ACを底辺として面積を求めると
4√5×BG×1/2
①より、
BG＝8√5/5 ー②
四角形CDIHはCD＝IH、CD//IHの平行四辺形なので
底面CDIHの体積は
ID×AD＝9/2×4√5＝18√5 ー③
②、③より求める体積は
8√5/5×18√5×1/3＝48
大問4
問題文
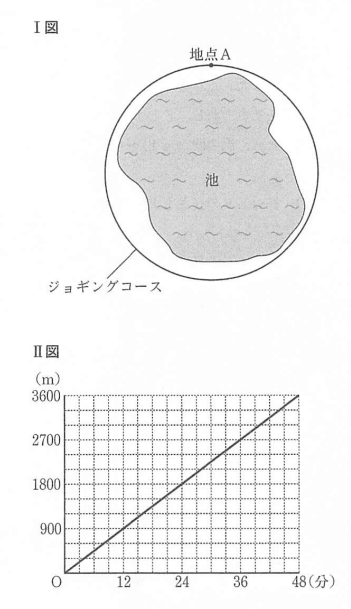
Ⅰ図のように、池のまわりに1周1800ｍの円形のジョギングコースがあり、このジョギングコース上に地点Aがある。ひなたさんは、午前9時ちょうどに地点Aを出発し、このジョギングコースを、一定の速さで同じ向きに2周歩いて、午前9時48分ちょうどに地点Aに着いた。
また、大輝さんは、ひなたさんと同時に地点Aを出発し、このジョギングコースを、一定の速さでひなたさんと同じ向きに1周走って、地点Aに着いたところで18分間休憩した。休憩後、再び地点Aを出発し、1周目と同じ一定の速さで、1周目と同じ向きにもう1周走って、午前9時36分ちょうどに地点Aに着いた。
Ⅱ図は、午前9時から午前9時48分における、ひなたさんが午前9時に地点Aを出発してからの時間と、ひなたさんが午前9時に地点Aを出発してから進んだ道のりとの関係をグラフに表したものである。
このとき、次の問い(1)～(3)に答えよ。
（1）午前9時から午前9時36分における、大輝さんが午前9時に地点Aを出発してからの時間と、大輝さんが午前9時に地点Aを出発してから進んだ道のりとの関係を表すグラフを答案用紙にの図にかけ。
（2）大輝さんが、休憩後、ひなたさんに追いついたのは午前9時何分何秒か求めよ。ただし、分、秒いずれも0以上59以下の整数で答えること。
（3）京平さんは、午前9時29分ちょうどに地点Aを出発し、このジョギングコースを、一定の速さでひなたさんと反対向きに1周走って、午前9時41分ちょうどに地点Aに着いた。このとき、京平さんが、大輝さんとすれ違ってから、ひなたさんとすれ違うまでに進んだ道のりを求めよ。
解答・解説
（1） 【正答 】
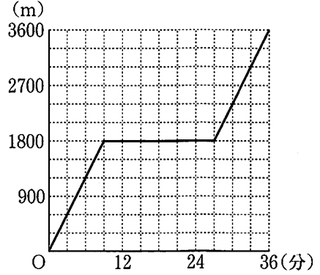
大輝さんが走った時間は
36分－18分＝18分
1周にかかる時間は、18分÷2＝9分
（2） 【正答 午前9時28分48秒】
Ⅱ図と(1)のグラフを照らし合わせる。
(1)のグラフのｘの変域が27≦ｘ≦36のときに、大輝さんとひなたさんがすれ違う。
(1)のグラフで27≦ｘ≦36のときのグラフの傾きは
(3600-1800)/(36-27)=200
y=200x+bに(27,1800)を代入し
y=200x-3600 ー①
また、Ⅱ図のグラフの傾きは
(3600-0)/(48-0)=75
原点を通るので
y=75x ー②
大輝さんとひなたさんがすれ違う時間は①、②より
200x-3600=75x
⇔x=28.8分=28分48秒
（3） 【正答 350ｍ】
京平さんの地点Aを出発してから進んだ道のりとの関係をⅡ図のようにグラフで表すと、
ひなたさんと反対向きに進んでいるので(41,1800)、(29,3600)のように座標をとることができる。
グラフの傾きは
(3600-1800)/(29-41)=-150
y=-150x+bに(41,1800)を代入し
y=-150x+7950 ー③
大輝さんと京平さんがすれ違う時間は①、③より
200x-3600=-150x+7950
⇔x=33分
このときの京平さんのy座標は
y=-150×33+7950=3000ⅿ －④
ひなたさんと京平さんがすれ違う時間は①、③より
75x=-150x+7950
⇔x=106/3
このときの京平さんのy座標は
y=-150×106/3+7950=2650ⅿ ー➄
④、➄より
3000ⅿ-2650ⅿ=350ｍ
大問5
問題文
図のように、△ABCがあり、AB＝9㎝、BC＝7㎝である。
∠ABCの二等分線と∠ACBに二等分線との交点をⅮとする。また、点Ⅾを通り辺BCに平行な直線と2辺AB、ACとの交点をそれぞれE、Fとすると、BE＝3㎝であった。
このとき、次の問い(1)～(3)に答えよ。
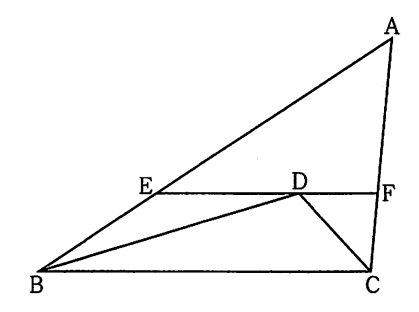
（1）線分EFの長さを求めよ。
（2）線分AFの長さを求めよ。
（3）△CFDと△ABCの面積の比を最も簡単な整数の比で表せ。
解答・解説
（1） 【正答 14/3】
EF//BCより
EF：BC＝AE：AB＝9-3：9＝2：3 より
EF：7＝2：3
⇔EF＝14/3
（2） 【正答 10/3】
問題文と EF//BCから錯角は等しいので
∠EBD＝∠DBC＝∠EDB
∠DCF＝∠DCB＝∠FDC
より△BDE、△CDFＨはそれぞれEB＝ED、FC＝FDの二等辺三角形。
ED＝3㎝となるので、
DF＝EF-ED＝14/3-3＝5/3＝CF
(1)から
AF：FC＝2：1
AF：5/3＝2：1
⇔AF＝10/3
（3） 【正答 △CFD：△ABC＝5：63】
△ABCの面積を１とする
高さが同じ場合、底面の比と面積の比が等しくなるので、
△ACE＝△ABC×AE/AB＝1×6/9＝2/3
△CEF＝△ACE×FC/AC＝2/3×(5/3)/(15/3)＝2/3×1/3＝2/9
△CFD＝△CEF×DF/EF＝2/9×(5/3)/(14/3)＝2/9×5/14＝10/126＝5/63
よって、
△CFD：△ABC＝5/63：1＝5：63
大問6
問題文
同じ大きさの正三角形の板がたくさんある。これらの板を、重ならないようにすき間なくしきつめて、大きな正三角形を作り、上の段から順に1段目、2段目、3段目、…とする。右の図のように、1段目の正三角形の板には1を書き、2段目の正三角形の板には、左端の板から順に2、3、4を書く。3段目の正三角形の板には、左端の板から順に5、6、7、8、9を書く。4段目以降の正三角形の板にも同じように、連続する自然数を書いていく。たとえば、4段目の左端の正三角形の板に書かれている数は10であり、4段目の右端の正三角形の板に書かれている数は16である。
このとき、次の問い(1)・(2)に答えよ。
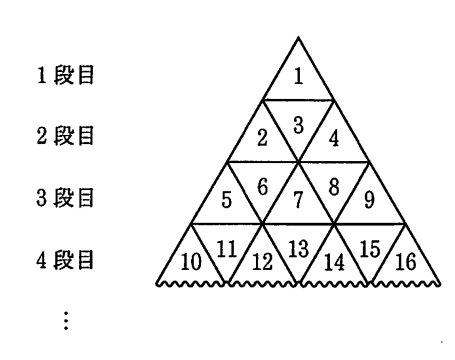
（1）7段目の左端の正三角形の板に書かれている数を7段目の右端の正三角形の板に書かれている数をそれぞれ求めよ。
（2）n段目の左端の三角形の板に書かれている数とn段目の右端の正三角形の板に書かれている数の和が1986であった。このとき、nの値を求めよ。
解答・解説
（1） 【正答 (7段目の左端の正三角形の板に書かれている数) 37
（7段目の右端の正三角形の板に書かれている数）49 】
右端の正三角形の板に書かれている数は、(段の数)²となっている。
7段目の右端は、7²=49
7段目の左端の正三角形の板に書いてある数は、6段目の右端に1を足した数なので、
6²+1＝37
（2） 【正答 32】
n段目の左端の正三角形の板に書かれている数は(n-1)²+1
n段目の右端の正三角形の板に書かれている数はn²
(n-1)²+n²=1986
n≧0なので
n=32
志望校に合わせた受験対策なら、やる気アシストにお任せ下さい！
家庭教師のやる気アシストは、京都府にお住まいの受験生のお子さんを毎年たくさん指導をさせ頂き、合格に導いています。
おかげさまで、昨年度の合格率は、関西エリア全体で97.3％という結果を残すことが出来ました。
高い合格率の秘訣は、指導経験豊富な先生の指導力に加え、1対1の指導でお子さん一人ひとりの状況に合わせた、お子さんだけのカリキュラムで勉強が進められるから！
家庭教師のやる気アシストは、お子さんの志望校合格まで全力でサポートさせて頂きます！
0120-740-100
LINE問合せ窓口
LINEからもお問合せいただけます！
公式Instagram
勉強のお役立ち情報を配信中！
お問い合わせ、ご質問も受付中です！
ご質問などお気軽にお問い合わせください。
アシストの指導方法がじっくり見れる！知れる！無料の体験授業実施中
お子さんにとって「成果が出る勉強法」ってどんな勉強法だと思いますか？
お子さんそれぞれに、個性や性格、学力の差もあります。そんな十人十色のお子さん全員に合う勉強法ってなかなかないんです。
たからこそ、受験生の今だけでもお子さんだけの勉強法で受験を乗り越えてみませんか？
やる気アシストには、決まったカリキュラムはありません。お子さんの希望や学力、得意や不得意に合わせて、お子さんだけのカリキュラムで指導を行っていきます。また、勉強法もお子さんそれぞれに合う合わないがあります。無料体験授業では、お子さんの性格や生活スタイルを見せていただき、お子さんにとって効率的な成果の出る勉強のやり方をご提案させて頂きます。
