【京都府】令和6年度/2024年度入学者高校入試選抜試験：数学の解説
京都府の2024年3月実施の令和6年度（2024年度）入学者の公立高校入試問題の解説をしています。
受験勉強において、過去問を解くことはとても効果的な勉強法です。ぜひ、受験までに一度挑戦し、問題の傾向を掴んでおきましょう。合わせて、対策などをたてられるととても良いですね。
また、過去問で苦手な点が見つかった場合は、そこを中心に試験日当日までにしっかりと対策しておきましょう。
大問1
問題文
(1) 6－２×(－5)² を計算せよ。
(2) 2/3( 6x + 3y )－1/4( 8x－2y ) を計算せよ。
(3) √32－16/√2＋√18
(4) ｘ＝7、ｙ＝－6 のとみ、(ｘ－ｙ)²－10(ｘ－ｙ)＋25 の値を求めよ。
(5) 2次方程式 8ｘ²＝22ｘ を解け。
(6) ｙはｘの2乗に比例し、ｘ＝３のときｙ＝－54 である。このときｙをｘの式で表せ。
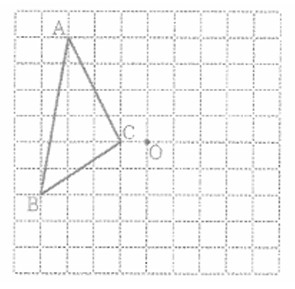
(7) 右の図のように、方眼紙上に△ABCと点Oがあり、4点A、B、C、Oは方眼紙の縦線と横線の交点上にある。△ABCを、点Oを回転の中心として、時計回りに270°だけ回転移動させた図形を、答案用紙の方眼紙上にかけ。
(8) 赤玉が2個、白玉が2個、黒玉が1個の合計5個の玉が入っている袋がある。この袋から玉を1個取り出し、取り出した玉を袋にもどさずに、玉をもう1個取り出す。このとき、取り出した2個の玉の色が異なる確率を求めよ。ただし、袋に入っているどの玉が取り出されることも同様に確からしいものとする。
解答・解説
(1) 6－2×(－5²) ＝ 6 + 50 = 56
(2) 2/3(6x＋3y) － 1/4(8x－2ｙ)
＝(4x＋2y)－(2ｘ－y/2)
＝2ｘ＋5/2y
(3) √32－16/√2＋√18
＝4√2－8√2＋3√2
＝－√2
(4) (x－y)＝A とすると、
(x－y)²－10(x－y)＋25＝A ²―10A＋25＝ (A ―5)²と変形することができる。
x－y=7－(ー6)＝13なので、
( 13―5 ) ²＝8²
＝64
(5) 8x²－22x＝0
2x(4x－11)＝0 と変形することができ、x＝0、11/4
(6) yはx²に比例するから、y＝ax²
これにx＝3、y＝－54を代入すると、－54＝a×3²
よって、a＝－6
y＝－6x²
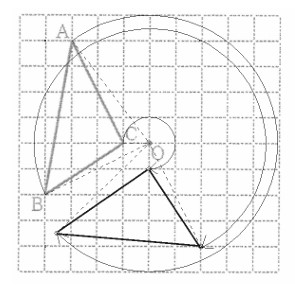
(7) 図のようにそれぞれの点と中心Oを結んでそれらを270 回転させて描く
(8) 1個目に赤玉、白玉、黒玉をとり出す確率はそれぞれ、赤：2/5、白：3/4、黒：4/4
それぞれで2個目にとり出す玉の色が異なる確率は、1個目が赤：3/4、白：3/4、黒：4/4
したがって、求める確率は、(2/5×3/4)＋(2/5×3/4)＋(1/5×4/4)=3/10+3/10+2+10=8/10=4/5
大問2
問題文
ある中学校の2年生は、 A組、 B組、 C組、 D組の4学級で編制されており、各学級の人数は30人である。 この中学校では、家庭でのタブレット端末を活用した学習時間を調査しており、その結果から得られた学習時間のデータをさまざまな方法で分析している。 右のⅠ図は、2年生の120人
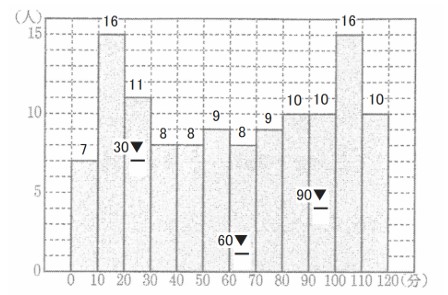
全員のある日の学習時間を調査した結果を、ヒストグラムに表したものである。 たとえば、Ⅰ図から、 2年生の120人のうち、学習時間が0分以上10分未満の生徒は7人いることがわかる。
このとき、次の問い(1)・(2) に答えよ。
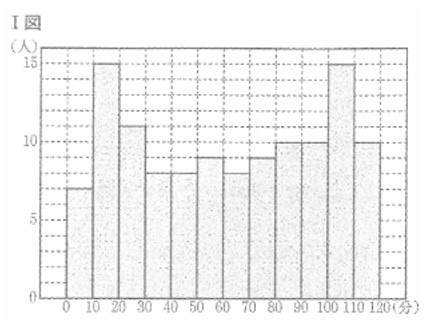
(1) Ⅰ図において、学習時間が30分以上90分未満の生徒は何人いるか求めよ。 また、右の ア～エの箱ひげ図のいずれかは、Ⅰ図のヒストグラムに対応している。Ⅰ図のヒストグラムに対応している箱ひげ図を、 ア～エから1つ選べ。
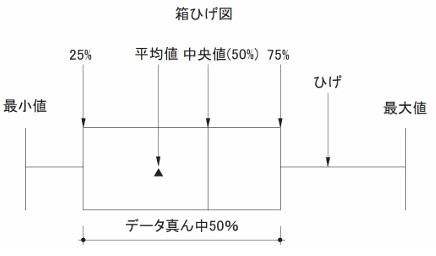
(2) Ⅱ図は、 Ⅰ図のもととなった学習時間の調査結果を、学級ごとに箱ひげ図に表したものである。 Ⅱ 図 から必ずいえるものを、次のア～オから 2つ 選べ。
ア A組は、学習時間が60分以上 70分未満の生徒が1人以上いる。
イ B組は、学習時間が80分以上の生徒が8人以上いる。
ウ C組は、学習時間が115分の生徒が1人だけいる。
エ 4学級のうち、 D組は、学習時間が0分以上 40分未満の生徒の人数が最も多い。
オ 4学級のうち、学習時間のデータの四分位範囲が最も大きい学級は、学習時間のデータの範囲が最も小さい。
解答・解説
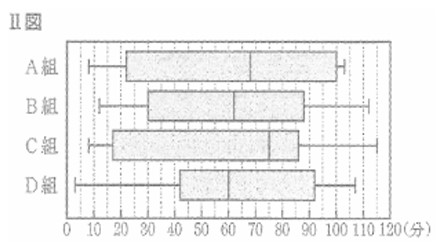
(1) 52人，ア
下の図から30分以上90分未満の生徒は52人
(2) イ，オ
大問3
問題文
AさんとBさんは、水泳、自転車、長距離走の3種目を、この順に連続して行うトライアスロンの大会に参加した。スタート地点から地点Pまでが水泳、地点Pから地点Qまでが自転車、 地点Qからゴール地点までが長距離走で、スタート地点からゴール地点までの道のりは14300mであった。
AさんとBさんは同時にスタートし、どちらも同じ速さで泳ぎ、6分後に地点Pに到着した。地点Pから地点Qまで、Aさんは分速600m、Bさんは分速 500mでそれぞれ走り、AさんはBさんより早く地点Qに到着した。Aさんは、地点Qからゴール地点まで走っている途中でBさんに追いつかれ、その後、Bさんより遅れてゴールした。地点Qからゴール地点までにおいて、Aさんが走る速さは、Bさんが走る速さの4/5倍であっ た。
右の図は、Aさんがスタートしてから3分後の、Aさんがスタート地点から進んだ道のりをｙmとして、 ｘとｙ の関係をグラフに表したものである。ただし、Aさん、Bさんともに、各種目で進む速さはそれぞれ一定であり、種目の切り替えにかかる時間は考えないものとする。
このとき、次の問い(1)・(2)に答えよ。
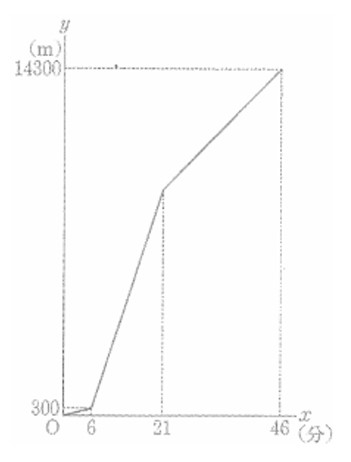
(1) 地点Pから地点Qまでの道のりは何m か求めよ。 また、21≦ｘ≦46のときのｙをｘの式で表せ。
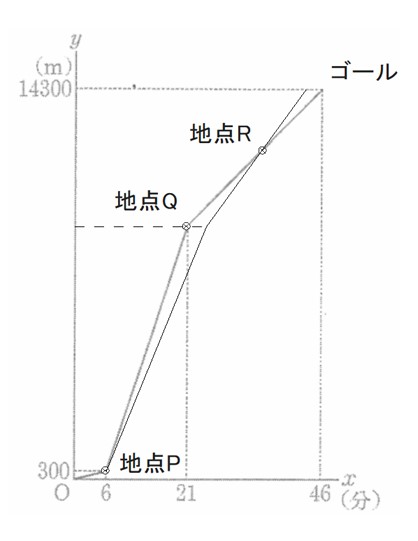
(2) 地点Qからゴール地点までにおいて、Aさんが走っている途中で、Bさんに追いつかれたときの、Aさんがスタート地点から進んだ道のりは何m か求めよ。
解答・解説
(1) 9000m, y＝200x＋5100
Aさんは地点Pから地点Qまで分速600mで15分間走った為、600×15＝9000mx＝21のとき、y＝300＋9000＝9300
x＝46のとき、y＝14300であるから、y＝ax＋b とすると、
9300＝21a＋b
14300＝46a＋bこれら2つの式を解くとa＝200, b＝5100
よって、y＝200x＋5100 ……①
(2) 12300m
Bさんが地点Qに到達した時間は 9000÷500＝18 より、x＝24分。
Aさんの走る速さは(1)より200m/分（傾き）。
また、Aさんの走る速さはBさんの5/4倍であるから、Bさんの走る速さは 200×5/4＝250m/分。
Bさんが地点Qからゴールまで走るときのグラフの式を y＝250x＋c とすると、これが(24,9300)を通ることから、9300＝250×24＋c より c＝3300。
したがって、y＝250x＋3300 …②。
よって、地点Rは①と②の交点であるから、二つの式の連立方程式を解くと R(36,12300)。
求める道のりは12300m。
大問4
問題文
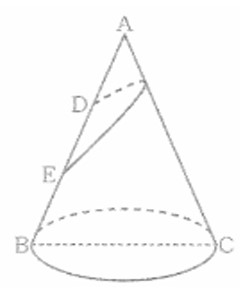
右の図のような、頂点をA、線分BCを直径とする円を底面とする円錐があり、高さは4√6 cm、AB : BC = 3 : 2である。 線分ABを3等分する点を点Aに近い方から順にD、Eとする。 また、この円錐の側面に、点Eから線分ACを通し、点Dまで、ひもをゆるまないようにかける。このとき、次の問い(1)・(2) に答えよ。
(1) この円錐の底面の半径を求めよ。 また、線分AEの長さを求めよ。
(2) かけたひもの長さが最短となるときの、ひもの長さを求めよ。 ただし、ひもの太さは考えないものとする。
解答・解説
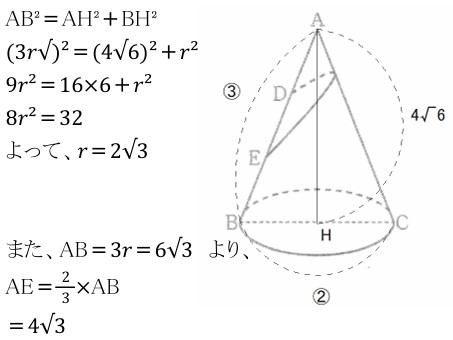
(1) 半径2√3 ，DE cm ＝4√3
AからBCに下した垂線とBCの交点をH、半径をrとすると
△ABHにおいて三平方の定理を利用して、
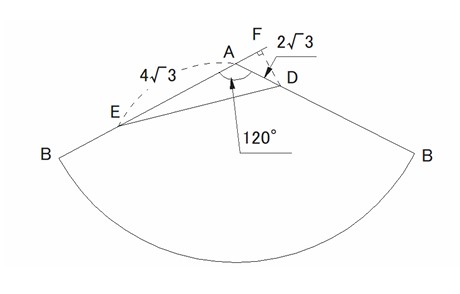
(2) DE cm ＝2√21
展開図は右の図のようになり、ABを延長した直線にDから下した垂線との交点をFとすると、
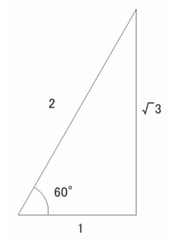
△DAFは∠DAF ＝60° の直角三角形であるから
AF＝√3 ，DF ＝3
EF ＝4√3＋√3
EF ＝5√3
△DEFにおいて、三平方の定理を利用すると、
DE²＝ EF² ＋DF²
DE² ＝ ( 5√3 ) ²＋3²
DE² ＝75＋9
DE²＝84 DE＝2√21cm
0120-740-100
LINE問合せ窓口
LINEからもお問合せいただけます！
公式Instagram
勉強のお役立ち情報を配信中！
お問い合わせ、ご質問も受付中です！
ご質問などお気軽にお問い合わせください。
大問5
問題文
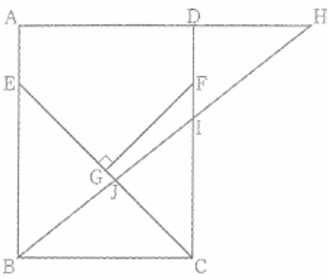
右の図のような、AB = 8cm、AD = 6cmの長方形ABCDがある。点Eを、辺AB上にAE = 2cm となるようにとり、線分CEの垂直二等分線と辺CD、線分CEとの交点をそれぞれF、Gとする。 また、
DH = 4cm となるような点Hを、辺ADを延長した直線上にとり、2点B、Hを通る直線と辺 CD、線分CEとの交点をそれぞれI、Jとする。
このとき、次の問い(1)～(3)に答えよ。
(1) △CFGの面積を求めよ。
(2) 線分CIの長さを求めよ。
(3) 四角形FGJIの面積を求めよ。
解答・解説
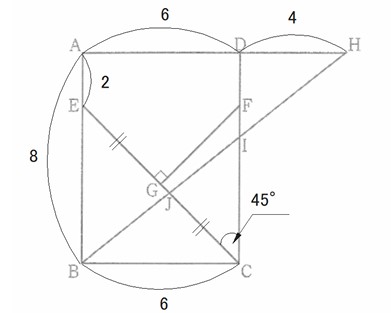
(1) 9㎠
△EBCはBC ＝ BEの直角二等辺三角形であるから
BC ＝6 ，EC ＝6√2
CG=1/2×EC
CG=3√2
∠GCF ＝45° であるから、求める面積は、 △EBC＝1/2×CG²＝1/2×(3√2)²＝9㎠
(2) 24/5 cm
△IDHと△ICBにおいて、∠IDH=∠ICB=90°
∠DIH ＝∠CIB より、△IDH∽△ICB
相似比は、DH：BC＝4：6
よって、CI＝ｔとすると、DI＝8－ｔなので、
( 8― ｔ) ︓ｔ＝4︓6 4 ｔ ＝6 ( 8―ｔ）よって、
ｔ＝24/5㎝
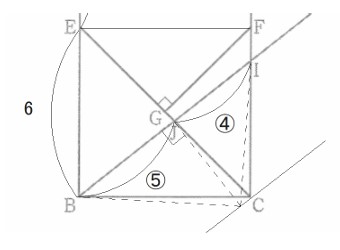
(3) 13/5 cm²
△JEBと△JCIにおいて、∠EJB ∠CJI、EB // CIより、 ∠JEB＝∠JCI、よって、△JEB∽JCI
相似比は、EB：CI＝6：24/5＝30：24＝5：4
よって、△CJIの面積は、△CBIの面積×4/9＝(6×24/5×1/2)×4/9＝22/5
したがって、求める四角形FGJIの面積は、△CFGの面積 △CBIの面積＝9－32/5＝13/5
大問6
問題文
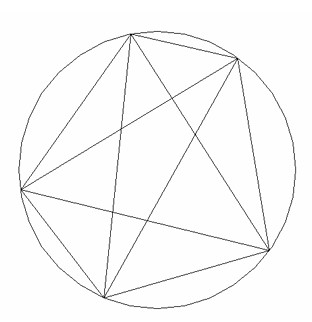
円周上に, 個の点をそれぞれ異なる位置にとり、これらのすべての点を互いに結ぶ線分をひき、弦の本数を考える。次の表は,ｎ = 2 , 3 , 4のときの、図と弦の本数をまとめたものである。
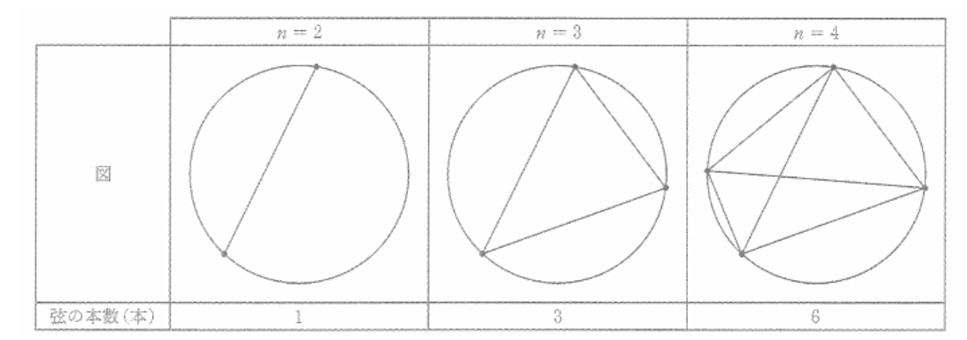
このとき、次の問い (1)～(3)に答えよ。 ただし、 ｎは2以上の自然数とする。
(1) ｎ＝５のとき、弦の本数を求めよ。
(2) ｎ＝41のとき、弦の本数を求めよ。
(3) 弦の本数が1953本であるときのｎの値を求めよ。
解答・解説
(1) 10本
1つの点から結べる弦の本数は、図のように4本となる。それぞれお互いの点でも重複していることを考慮すると5×4×1/2＝10本
(2) 820本
1つの点から結べる弦の本数は、(n ―1)本であるから弦の本数をyとすると、y ＝n×(n－1)×1/2と表 すことができる。
よって、ｎ＝41のとき、
41×40×1/2＝820本
(3) ｎ＝63
(2)の式にｙ＝1953を代入すると、1953＝n(n－1)×1/2
ｎ²－ｎ－3906＝0
(n＋62)(ｎ－63)＝0 ｎ＞0より、ｎ＝63
志望校に合わせた受験対策なら、やる気アシストにお任せ下さい！
家庭教師のやる気アシストは、京都府にお住まいの受験生のお子さんを毎年たくさん指導をさせ頂き、合格に導いています。
高い合格率の秘訣は、指導経験豊富な先生の指導力に加え、1対1の指導でお子さん一人ひとりの状況に合わせた、お子さんだけのカリキュラムで勉強が進められるから！
家庭教師のやる気アシストは、お子さんの志望校合格まで全力でサポートさせて頂きます！
LINE問合せ窓口
LINEからもお問合せいただけます！
公式Instagram
勉強のお役立ち情報を配信中！
お問い合わせ、ご質問も受付中です！
ご質問などお気軽にお問い合わせください。
アシストの指導方法がじっくり見れる！知れる！無料の体験授業実施中
お子さんにとって「成果が出る勉強法」ってどんな勉強法だと思いますか？
お子さんそれぞれに、個性や性格、学力の差もあります。そんな十人十色のお子さん全員に合う勉強法ってなかなかないんです。
たからこそ、受験生の今だけでもお子さんだけの勉強法で受験を乗り越えてみませんか？
やる気アシストには、決まったカリキュラムはありません。お子さんの希望や学力、得意や不得意に合わせて、お子さんだけのカリキュラムで指導を行っていきます。また、勉強法もお子さんそれぞれに合う合わないがあります。無料体験授業では、お子さんの性格や生活スタイルを見せていただき、お子さんにとって効率的な成果の出る勉強のやり方をご提案させて頂きます。
