京都府の2025年3月実施の令和7年度（2025年度）入学者の公立高校入試問題の解説をしています。
受験勉強において、過去問を解くことはとても効果的な勉強法です。ぜひ、受験までに一度挑戦し、問題の傾向を掴んでおきましょう。合わせて、対策などをたてられるととても良いですね。
また、過去問で苦手な点が見つかった場合は、そこを中心に試験日当日までにしっかりと対策しておきましょう。

 京都府の公立高校入試情報はこちら

大問1

問題文

次の問い（ 1 ）～（ 8 ）に答えよ。

（ 1 ）11-(1/2-1)×(-2)²計算せよ。

（ 2 ）5x-1/6–x+2/12を計算せよ。

（ 3 ） (8-√8)(1+√8)を計算せよ。

（ 4 ） 半径 9 cm，弧の長さ 10πcm のおうぎ形の中心角の大きさを求めよ。

（ 5 ） 次の連立方程式を解け。
x=-9y-3
1/3x=3y+3

（ 6 ）ax^² – 5 ax – 24 a を因数分解せよ。

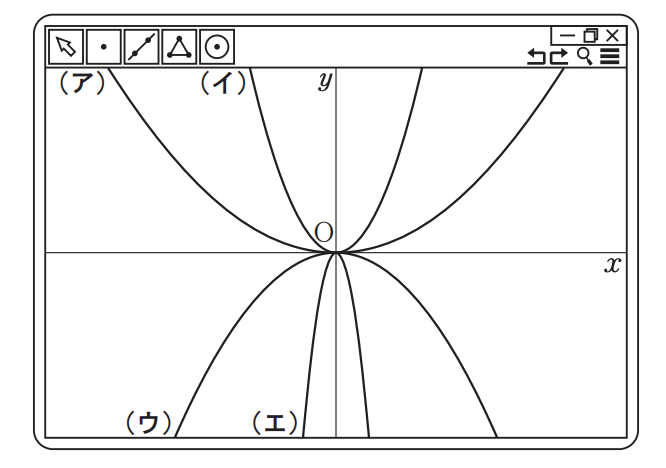
（ 7 ） 右の図は，グラフ作成ソフトウェアで 4 つの関数のグラフを表示させた，コンピュータの画面を表した ものであり，（ア）～（エ）はそれぞれ，関数 y = x²， y=1/7x²，y =-7x²，y = -2/7x² のグラフのい ずれかである。図中の（ア）～（エ）のうち，関数y = -2/7x² のグラフにあたるものとして最も適当 なものを 1 つ選べ。

（ 8 ） 次の資料は，ある中学校の 3 年生 9 人の反復横とびの記録をまとめたものである。この資料について，3 年生 の記録の四分位範囲を求めよ。

解答・解説

（1）$13$
計算の順番に注意しましょう。
$（与式）=11-(-\frac{1}{2})\times4=11+2=13$

（2）$\frac{11x-4}{12}$
分母をそろえて計算しましょう。
$（与式）=\frac{{2(5x-1)}-(-x+2)}{12}=\frac{10x-2+x-2}{12}=\frac{11x-4}{12}$

（3）$14\sqrt{2}$
$（与式）=8+8\sqrt{8}-\sqrt{8}-8=7\sqrt{8}=14\sqrt{2}$

（4）200°
おうぎ形の中心角をxとすると
$9\times2\timesπ\times\frac{x}{360}=10π$
$x=200$

（5）$x=3,y=-\frac{2}{3}$
代入法で解くとよいです。

（6）$a(x-8)(x+3)$
共通項をまとめていきます。
$（与式）=a(x^2-5x-24)=a(x-8)(x+3)$

（7）ウ
x²の係数がマイナスなのでウかエ。さらに$\-frac{2}{7}$の方が$-7$よりも開きが大きくなるのでウが答えです。

（8）$12$点
四分位範囲とは第3四分位数から第1四分位数を引いたものです。
記録を小さい順にすると、35，41，43，45，48，50，52，56，57になります。
よって、第1四分位数は$\frac{41+43}{2}=42$、第3四分位数は$\frac{52+56}{2}=54$
四分位範囲は$54-42=12$

大問2

問題文

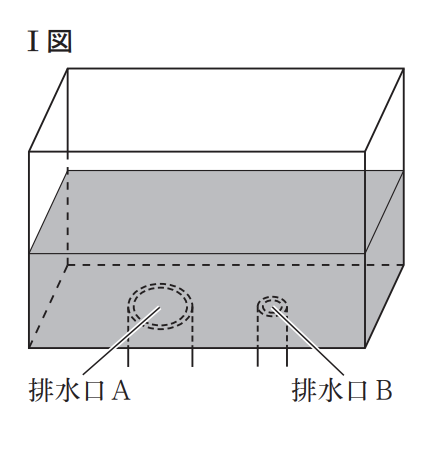
右のⅠ図のように，排水口Ａ，Ｂがついている水そうがあり，排水口Ａ，Ｂは どちらも閉じた状態で，水そうには40Lの水が入っている。排水口Ａを開くと毎分4Lの割合で水そうから水が出て，排水口Ｂを開くと毎分 1Lの割合で水そ うから水が出る。 
優さんは，ストップウォッチとⅠ図の水そうを用いて，次の〈操作〉を行った。

〈操作〉
手順①　排水口Ａを開くと同時にストップウォッチをスタートさせる。
手順②　手順①でストップウォッチをスタートさせてからちょうど 2 分後 に，排水口Ａを閉じると同時に排水口Ｂを開く。 
手順③ 　手順②で排水口Ｂを開いてからちょうど 4 分後に，排水口Ｂは開い たままの状態で，再び排水口Ａを開く。 
手順④ 　手順③で排水口Ａを開いてからちょうど 4 分後に，排水口Ａ，Ｂを 同時に閉じる。

このとき，次の問い（ 1 ）・（ 2 ）に答えよ。

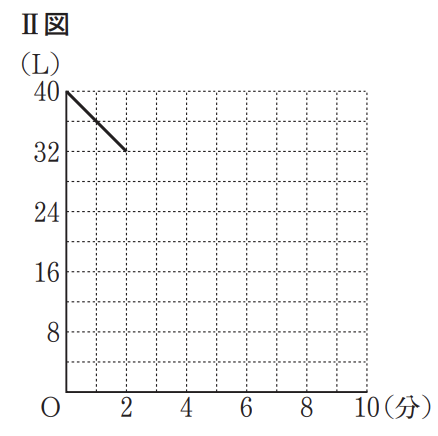
（ 1 ）次のⅡ図は，〈操作〉において，優さんがストップウォッチをスタートさせてから排水口Ａ，Ｂを同時に閉じ るまでの，時間と水そう内の水の量の関係を表したグラフの一部であり，途中までかいてある。答案用紙の図に続きをかき入れて，ストップウォッチをスタートさせてから排水口Ａ，Ｂを同時に閉じるまでのグラフを完成させよ。

（ 2 ） 〈操作〉において，水そう内の水の量がちょうど 15Lであったのは，優さんがストップウォッチをスタートさせてから何分何秒後か求めよ。ただし，分，秒いずれも 0 以上 59 以下の整数で答えること。 

解答・解説

（1）略
2分後～6分は排水溝Bだけが開いているので毎分1Lの割合で水が出るため、(6,28)までを結ぶ。
6分後～10分は排水溝AとBが開いているので毎分5Lの割合で水が出るため、（10,8）までを結ぶ。

（2）8分36秒後
前問のグラフより15Lだった時は手順③の時だったと分かるので、この式を求めると
$y=-5x+58$となります。この時y=15のときのxの値が答えになるので
$-5x+58=15$
$x=\frac8{3}{5}$となります。$60\times\frac{3}{5}=36$なので、答えは8分36秒後です。

大問3

問題文

図のように，1 ，4 ，7 の数が1つずつ書かれた 3 個の玉が入っている袋Ａと，0 ，5 ，10 の数が 1 つずつ書かれた 3 個の玉が 入っている袋Ｂと，2 ，3 の数が 1 つずつ書かれた2個の玉が入っている袋Ｃがある。それぞれの袋から1個ずつ玉を取り出し，袋Ａから取り出した玉に書かれている数をa，袋Ｂから取り出した玉に 書かれている数をb，袋Ｃから取り出した玉に書かれている数をcとする。

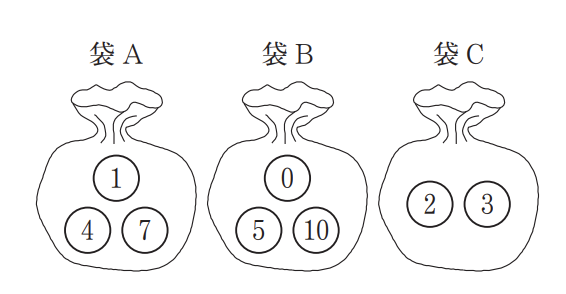
このとき，次の問い（ 1 ）・（ 2 ）に答えよ。ただし，それぞれの袋において，どの玉が取り出されることも同様に 確からしいものとする。

（ 1 ） a + b の値が c でわり切れる確率を求めよ。

（ 2 ） 6 a + 9 b + 6 の値が c でわり切れる確率を求めよ。

解答・解説

（1）$\frac{7}{18}$
2で割り切れる数はa+bの値が偶数のときなので、(1,5)(4,0)(4,10)(7,5)の4通り。
3で割り切れる数はa+bの値が3の倍数のときなので、(1,5)(4,5)(7,5)の3通り。
全通りは18通りなので、確率は$\frac{4+3}{18}=\frac{7}{18}$となります。

（2）$\frac{5}{6}$
2で割り切れる数は6a,9bが共に偶数になるときなので、(1,0)(1,10)(4,0)(4,10)(7,0)(7,10)の6通り
3で割り切れるときを考えると、因数分解を行い$6a+9b+6=3(2a+3b+2)$。
つまり、aとbがどんな数でも3の倍数となります。これらは9通りあるので
確率は$\frac{6+9}{18}=\frac{15}{18}=\frac{5}{6}$

大問4

問題文

図のように，三角錐すいＯＡＢＣがあり，ＯＣ = 9 cm，ＡＢ=ＢＣ=10 cm，ＡＣ=12 cm，∠ＯＣＡ=∠ＯＣＢ=90° である。頂点Ｂから辺ＡＣにひいた垂線と辺ＡＣとの交点をＤとする。また，線分ＡＤ上に点Ｅを，ＡＥ：ＥＤ = 2：1 となるようにとり，点Ｅを通り平面ＯＢＣに平行な平面と，2 辺ＯＡ，ＡＢとの交点をそれぞれＦ，Ｇとする。 

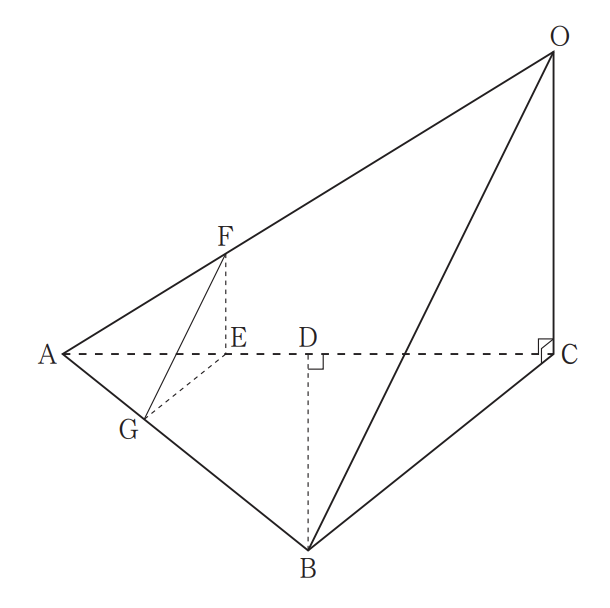
このとき，次の問い（ 1 ）～（ 3 ）に答えよ。

（ 1 ）線分ＢＤの長さを求めよ。

（ 2 ） △ＥＦＧの面積を求めよ。

（ 3 ）三角錐ＢＥＦＧの， △ＥＦＧを底面としたときの高さを求めよ。

解答・解説

（1）8ｃｍ
△ABC は BA = BC の二等辺三角形で，頂点 B から底辺 AC に下ろした垂線は底辺 AC を 2 等分するので、AD＝6ｃｍになります。
よって、△BDAに三平方の定理を用いると
$BD^2+6^2=10^2$
$BD^2=64$
BD>0なので
$BD=8cm$

（2）5ｃｍ²
仮定より△COB∽△EFG
AD：DC＝1：1、AE：ED＝2：1なので
AE：ED：DC＝2：1：3
よって、AE:EC＝2：(1+3)：2：4＝1：2
したがって、△COBと△EFGの相似比は
CO：EF＝CA：EA＝3：1
よって面積比は9：1です。
$△OBC=\frac{1}{2}\times10\times9=45$なので
$△EFG$=\frac{1}{9}△OBC=5cm^2$

（3）$\frac{32}{5}cm$
三角錐BEFGの体積を2通りの方法で求めます。
三角錐BEFGの体積をVとします。
➀底面を△BEGとすると、高さはEFです。
△BEGの面積はAG:GB＝1：2なので、$△BEG=\frac{2}{3}△ABE$
また、AE:AD＝2：3なので、$△ABE=\frac{2}{3}△ABD$
よって、$△BEG=\frac{2}{3}\times\frac{2}{3}△ABD=\frac{2}{3}\times\frac{2}{3}\times(\frac{1}{2}\times6\times8)=\frac{32}{3}$
また、高さEFはEF：CO＝1：3なので、EF:9＝1：3よって、$EF=\frac{9}{3}=3$
したがって$V=\frac{1}{3}\times△BEG\times EF=\frac{1}{3}\times\frac{32}{3}\times3=\frac{32}{3}$
➁底面を△EFGとしたときの高さをhとすると
$V=\frac{1}{3}\times△EFG\times h=\frac{1}{3}\times5\times h=\frac{5}{3}h$
➀、➁のVの値は等しいので
$\frac{32}{5}=\frac{5}{3}h$
$h=\frac{32}{5}cm$

大問5

問題文

図のように，四角形ＡＢＣＤがあり，ＡＢ = 3 √2 cm， ＢＣ= 7 cm，∠ＡＢＣ= 45° ，∠ＢＣＤ= 60° ，∠ＢＤＣ= 90° である。頂点Ａから辺ＢＣにひいた垂線と辺ＢＣ，対角線ＢＤ との交点をそれぞれＥ，Ｆとする。また，∠ＢＣＤの二等分線 と線分ＡＥ，対角線ＢＤ，線分ＤＥとの交点をそれぞれＧ， Ｈ，Ｉとする。 

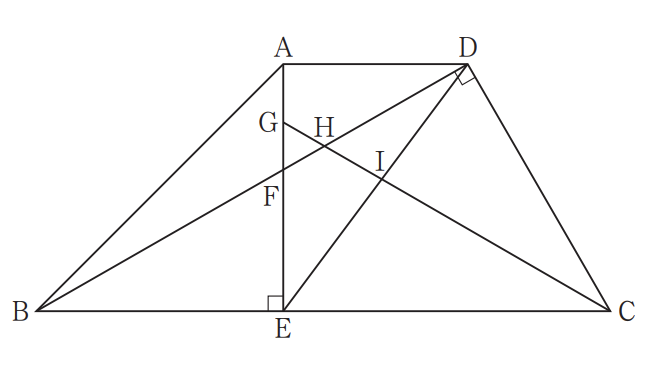
このとき，次の問い（ 1 ）～（ 3 ）に答えよ。

（ 1 ）線分ＣＥの長さを求めよ。

（ 2 ） 線分ＦＧの長さを求めよ。

（ 3 ） 四角形ＥＩＨＦの面積を求めよ。

解答・解説

（1）4ｃｍ
まずはBEをもとめて、BCから引けばよいです。
△ABEは1：1；√2の直角二等辺三角形なので、AB:BE＝√2：1
よって、$3\sqrt{2}:BE=\sqrt{2}:1$
$BE=3cm$
したがって、$CE=BC-BE=7-3=4cm$

（2）$\frac{\sqrt{3}}{3}cm$
GEからEFを引いて求めます。
△BEFは1：2：√3の三角形なので、BE:EF＝√3：1
よって、$3:EF=\sqrt{3}:1$
$EF=\frac{3}{\sqrt{3}}=\sqrt{3}$
また△CGEも同様にして、CE：EG＝√3：1
よって、$4:EG=\sqrt{3}:1$
$EF=\frac{4}{\sqrt{3}}=\frac{4\sqrt{3}}{3}$
これらより、$FG=EG-EF=\sqrt{3}-\frac{4\sqrt{3}}{3}=\frac{\sqrt{3}}{3}$

（3）$\frac{43\sqrt{3}}{60}cm^3$
△DEFの面積から△DHIの面積を求めます。
そのためにDI : IE; DH : HF，さらに4DEF の底辺を EF としたときの高さを求める必要があります。
(ⅰ)DI : IEを求めます。
直線CIは∠DCEの二等分線なので、DI:IE＝CD:CE…①
ここで、CD:BC:BD=1：2：√3なので、$CD:7:BD=1:2:\sqrt{3}$
$CD=\frac{7}{2}$…②、$BD=\frac{7\sqrt{3}}{2}$…③
➀に代入して、$DI:IE=\frac{7}{2}:4=7:8$
(ⅱ)DH:HFを求めます。
まず、直線CHが∠DCEの二等分線なので$DH:HB=DC:BC=\frac{7}{2}:7=1:2$…④
次にDF:FBを求めます。
点Dから線分BCに垂線DJを下すと△BJDの辺の比が1：2：√3になるので、DJ:DB＝1：2
したがって、③より
$DJ:\frac{7\sqrt{3}}{2}=1:2$
$DJ=\frac{7\sqrt{3}}{4}$…⑤
よって、DJ//FEより
$BF:BD=FE:DJ=4:7$
したがって、$BF:FD=4:3$…⑥
➃と⑥から点 H は線分 BD を 3 等分したうちの左から 2 つ分，点F は線分 BD を 7 等分したうちの左から 4 つ分。
3 等分と 7 等分では比べられないので，3 と 7 の最小公倍数 21 を考えて，線分 BD を 21 等分したと考えると$FH:HD=(14-12):7=2:7$
よって、$四角形EIHF＝△DEF-△DHI=△DEF-\frac{7}{2+7}\times\frac{7}{7+8}\times△DEF=\frac{86}{135}△DEF$
そして、△DEFの面積が底辺FEとすると高さはEJとなります。EJ=BJ-BEであり、DJ:JB＝1：√3なので⑤より$\frac{7\sqrt{3}}{4}:JB=1:\sqrt{3}$
$JB=\frac{7\sqrt{3}}{4}\sqrt{3}=\frac{21}{4}$
したがって、BE＝3なので
$EJ=BJ-BE=\frac{21}{4}-3=\frac{9}{4}$
これらより$四角形EIHF=\frac{86}{135}△DEF=\frac{43\sqrt{3}}{60}$

大問6

問題文

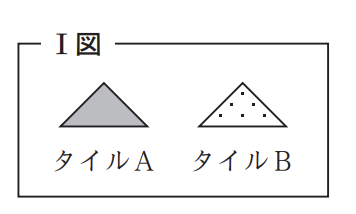
Ⅰ図のような，タイルＡとタイルＢが，それぞれたくさんある。タイルＡと タイルＢを，次のⅡ図のように，すき間なく規則的に並べたものを，1 番目の図形， 2 番目の図形，3 番目の図形，4 番目の図形，…とする。 
たとえば，3 番目の図形において，タイルＡは 24 枚，タイルＢは 12 枚である。

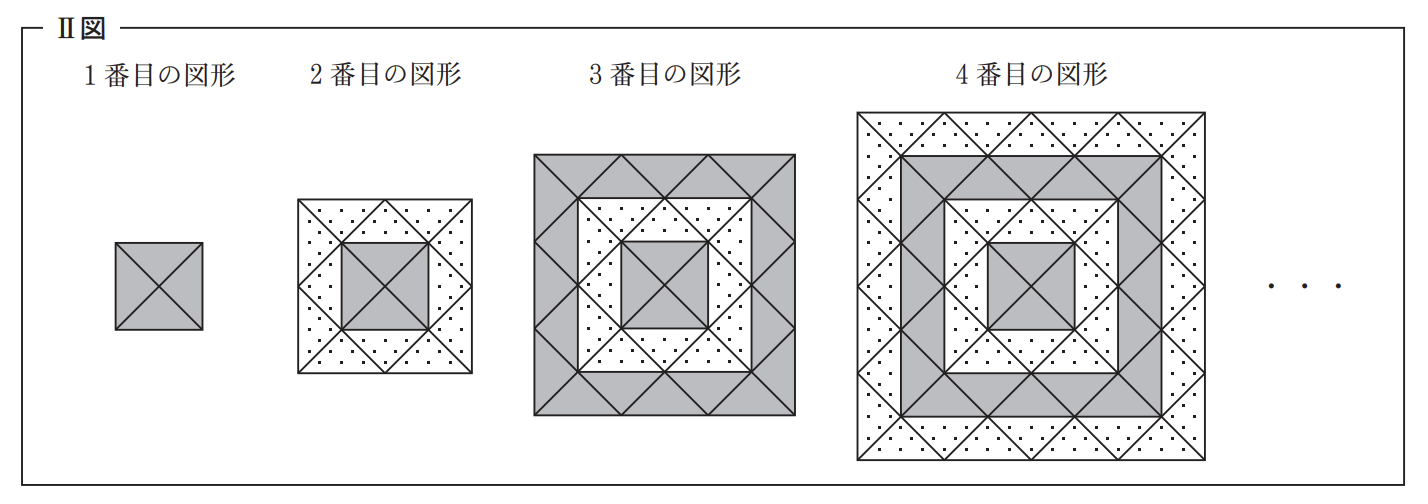
このとき，次の問い（ 1 ）・（ 2 ）に答えよ。

（ 1 ）5 番目の図形のタイルＡの枚数と，6 番目の図形のタイルＢの枚数をそれぞれ求めよ。

（ 2 ）n番目の図形のタイルＡの枚数とタイルＢの枚数の和が 3600 枚であるときのnの値を求めよ。また，このときのタイルＡの枚数を求めよ。

解答・解説

（1）84枚
5 番目の図形のタイル A の枚数は，内側から外側へ順に足していくと
$1\times4+5\times4+9\times4=60$枚
6 番目の図形のタイル B の枚数は，内側から外側へ順
に足していくと
$3\times4+7\times4+11\times4=84$枚

（2）1740枚
n番目の図形のタイルAの枚数とタイルBの枚数の合計は$(2\times n)^2$枚で、これが3600枚なので
$(2\times n)^2=3600$
$n^2=900$
n>0なので
$n=30$
よって、タイルAの枚数は
$1\times4+5\times4+9\times4+…+57\times4=4(1+5+9+…+57)=4\frac{1}{2}\times(58+58+…+58)=4\frac{1}{2}\times58\times15=1740$枚

 京都府のその他の過去問を見る

志望校に合わせた受験対策なら、やる気アシストにお任せ下さい！

家庭教師のやる気アシストは、大阪府にお住まいの受験生のお子さんを毎年たくさん指導をさせ頂き、合格に導いています。

高い合格率の秘訣は、指導経験豊富な先生の指導力に加え、1対1の指導でお子さん一人ひとりの状況に合わせた、お子さんだけのカリキュラムで勉強が進められるから！
家庭教師のやる気アシストは、お子さんの志望校合格まで全力でサポートさせて頂きます！

 アシストの受験対策をもっとみる

アシストの指導方法がじっくり見れる！知れる！無料の体験授業実施中

お子さんにとって「成果が出る勉強法」ってどんな勉強法だと思いますか？
お子さんそれぞれに、個性や性格、学力の差もあります。そんな十人十色のお子さん全員に合う勉強法ってなかなかないんです。
たからこそ、受験生の今だけでもお子さんだけの勉強法で受験を乗り越えてみませんか？

やる気アシストには、決まったカリキュラムはありません。お子さんの希望や学力、得意や不得意に合わせて、お子さんだけのカリキュラムで指導を行っていきます。また、勉強法もお子さんそれぞれに合う合わないがあります。無料体験授業では、お子さんの性格や生活スタイルを見せていただき、お子さんにとって効率的な成果の出る勉強のやり方をご提案させて頂きます。