







宮城県の2023年3月実施の令和5年度(2023年度)入学者の公立高校入試問題の解説をしています。
受験勉強において、過去問を解くことはとても効果的な勉強法です。ぜひ、受験までに一度挑戦し、問題の傾向を掴んでおきましょう。合わせて、対策などをたてられるととても良いですね。
また、過去問で苦手な点が見つかった場合は、そこを中心に試験日当日までにしっかりと対策しておきましょう。
次の(1)~(8)の問いに答えなさい。
(1)$-9+2$ を**計算しなさい。
(2)$-15 \div (-\frac{5}{3})$ を計算しなさい。
(3)110を素因数分解しなさい。
(4)等式 $4a – 9b + 3 = 0$ を $a$ について解きなさい。
(5)連立方程式 $\begin{cases} 3x – y = 17 \\ 2x – 3y = 30 \end{cases}$ を解きなさい。
(6)$\sqrt{54} + \frac{12}{\sqrt{6}}$ を計算しなさい。
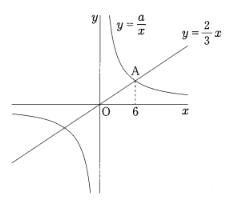
(7)下の図のように、比例 $y = \frac{2}{3}x$ のグラフと反比例 $y = \frac{a}{x}$ のグラフとの交点のうち、$x$座標が正である点をAとします。点Aの$x$座標が6のとき、$a$の値を求めなさい。
(8)ある学年のA組、B組、C組は、どの組にも35人の生徒が在籍しています。
これら3つの組の各生徒を対象に、1か月間に図書室から借りた本の冊数を調べました。下の図は、組ごとに、各生徒が借りた本の冊数の分布のようすを箱ひげ図に表したものです。
この箱ひげ図から必ずいえることを、 あとのア~工から1つ選び、記号で答えなさい。
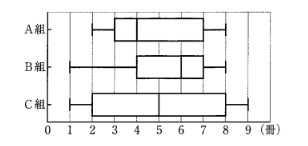
ア:第1四分位数は、A組とB組で同じである。
イ:四分位範囲が最も小さいのは、A組である。
ウ:借りた本の冊数が6冊以上である人数は、B組が最も多い。
エ:借りた本の冊数が2冊以上8冊以下である人数は、C組が最も多い。
(1)-7
$-9+8=-7$
(2)9
$-15 \times (-\frac{5}{3}) = -15 \times (-\frac{5}{3}) = 9$
(3)$2 \times 5 \times 11$
$110 = 2 \times 55 = 2 \times 5 \times 11$
(4)$a = \frac{9}{4}b – \frac{3}{4}$
$4a – 9b + 3 = 0$ から移項して $4a = 9b – 3$ だから両辺を4で割ると答えが得られる。
(5)$x=3, y=-8$
$3x-y=17 \cdots(1)$, $2x-3y=30 \cdots(2)$ とすると、$(1)\times3-(2)$より$7x=21$だから$x=3$
これを(1)に代入すると$3 \times 3 – y = 17$より$y=-8$
(6)$5\sqrt{6}$
$\sqrt{54} + \frac{12}{\sqrt{6}} = \sqrt{3^2 \times 6} + \frac{12 \times \sqrt{6}}{\sqrt{6} \times \sqrt{6}} = 3\sqrt{6} + \frac{12\sqrt{6}}{6} = 3\sqrt{6} + 2\sqrt{6} = 5\sqrt{6}$
(7)24
Aの$x$座標は6で、直線$y=\frac{2}{3}x$上にあるからAの$y$座標は$\frac{2}{3}\times6=4$である。
ここで、A(6,4)は反比例のグラフ$y=\frac{a}{x}$上にあるので$4=\frac{a}{6}$から$a=24$が求まる。
(8)ウ
ア:A組の第1四分位数は3で、B組の第1四分位数は4なので不適。
イ:四分位範囲はそれぞれA組:$7-3=4$, B組:$7-4=3$, C組:$8-2=6$なのでB組が最も小さく、不適。
ウ:B組の中央値が6であることから18人以上の生徒が6冊以上借りていることがわかる。一方で他クラスは中央値がそれより小さいことから6冊借りた生徒は18人より少ないことが分かり、適する。
エ:A組は全員が2冊以上8冊以下借りている一方で、C組は1冊借りた人や9冊借りた人がいるので、借りた本の冊数が2冊以上8冊以下である人数が最も多いのはC組でなくA組なので不適。
(1)下の図のような、半径が4cm、中心角が120°のおうぎ形OABがあります。点Aを通って線分OAに垂直な直線と、点Bを通って線分OBに垂直な直線をひき、その交点をCとします。次の①、②の問いに答えなさい。ただし、円周率を$\pi$とします。
(1)下の図のような、半径が4cm、中心角が120°のおうぎ形OABがあります。点Aを通って線分OAに垂直な直線と、点Bを通って線分OBに垂直な直線をひき、その交点をCとします。
次の①、②の問いに答えなさい。ただし、円周率を$\pi$とします。
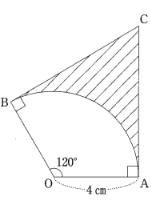
① 弧ABの長さを求めなさい。
② 弧ABと線分AC、線分BCとで囲まれた斜線部分の面積を求めなさい。
(2)哲也さんと舞さんは、坂の途中にある A 地点からボールを転がしたときの、ボールの転がる時間と距離の関係を調べました。その結果、ボールが転がり始めてから$x$秒間に転がる距離を$y$mとしたとき、$x$と$y$の関係は、$y=\frac{1}{4}x^2$であることがわかりました。右の図は、そのときの$x$と$y$の関係を表したグラフです。次の①、②の問いに答えなさい。
① 関数 $y=\frac{1}{4}x^2$ について、$x$ の値が0から6まで増加するときの変化の割合を求めなさい。
(2)哲也さんと舞さんは、坂の途中にある A 地点からボールを転がしたときの、ボールの転がる時間と距離の関係を調べました。その結果、ボールが転がり始めてから$x$秒間に転がる距離を$y$mとしたとき、$x$と$y$の関係は、$y=\frac{1}{4}x^2$であることがわかりました。右の図は、そのときの$x$と$y$の関係を表したグラフです。
次の①、②の問いに答えなさい。
① 関数 $y=\frac{1}{4}x^2$ について、$x$ の値が0から6まで増加するときの変化の割合を求めなさい。
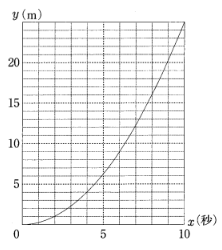
② 舞さんは、一定の速さで坂を下っています。舞さんが A 地点を通過するのと同時に、哲也さんは A 地点からボールを転がしました。ボールが転がり始めてから6秒後にボールは舞さんに追いつき、ボールが舞さんを追いこしてからは、舞さんとボールの間の距離はしだいに大きくなりました。
ボールが舞さんを追いこしてから、舞さんとボールの間の距離が18mになったのは、ボールが転がり始めてから何秒後ですか。
(3)赤球と白球がたくさん入っている箱の中に、赤球が何個あるかを推定します。 最初に箱の中にあった、赤球と白球の個数の比は4:1であったことがわかっています。 この箱に白球を300個追加し、箱の中の球をよくかき混ぜました。そのあと、120個の球を無作為に抽出したところ、赤球が80個ありました。この結果から、最初に箱の中にあった赤球は、およそ何個と考えられますか。
(4)下の図のように、100行3列のマス目がある表に、次の【規則】にしたがって、1から300までの自然数が1から順に、1つのマスに1つずつ入っています。ただし、表の中の・は、マスに入る自然数を省略して表したものです。
【規則】
1: 1行目は、1列目に1、2列目に2、3列目に3を入れる。
2:2行目以降は、1つ前の行に入れたもっとも大きい自然数より1大きい数から順に、次のとおり入れる。
偶数行目は、3列目、2列目、1列目の順で数を入れる。
奇数行目は、1列目、2列目、3列目の順で数を入れる。
たとえば、8は、3行目の2列目のマスに入っています。
次の①、②の問いに答えなさい。
(2)哲也さんと舞さんは、坂の途中にある A 地点からボールを転がしたときの、ボールの転がる時間と距離の関係を調べました。その結果、ボールが転がり始めてから$x$秒間に転がる距離を$y$mとしたとき、$x$と$y$の関係は、$y=\frac{1}{4}x^2$であることがわかりました。右の図は、そのときの$x$と$y$の関係を表したグラフです。
次の①、②の問いに答えなさい。
① 関数 $y=\frac{1}{4}x^2$ について、$x$ の値が0から6まで増加するときの変化の割合を求めなさい。
① 45 は、何行目の何列目のマスに入っていますか。
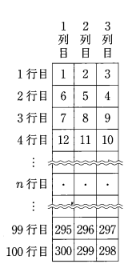
② $n$行目のマスに入っている3つの自然数のうち、もっとも小さいものをPとします。次の(ア)、(イ)の問いに答えなさい。ただし、$n$は1以上100以下とします。
(ア) 自然数Pを$n$を使った式で表しなさい。
(イ) nが2以上のとき、$n$行目の1つ前の行を$(n-1)$行目とします。$(n-1)$行目のマスに入っている3つの自然数のうち、もっとも大きいものをQとします。P+Q=349のとき、$n$行目の3列目のマスに入っている自然数を求めなさい。
(1)
① $\frac{8}{3}\pi$ cm
$2 \times \pi \times 4 \times \frac{120}{360} = \frac{8}{3}\pi$
② $16\sqrt{3} – \frac{16}{3}\pi$ cm$^2$
$OA=OB, \angle OAC = \angle OBC, OC共通だから直角三角形の斜辺と他の一辺が等しく、\triangle OAC \equiv \triangle OBCである。
よって\angle AOC = \angle BOCより\angle AOC = 60^\circ$ なので$AC = OA \times \sqrt{3} = 4\sqrt{3}$より$\triangle OAC = \frac{1}{2} \times 4 \times 4\sqrt{3} = 8\sqrt{3}$である。
$OAC \equiv \triangle OBC$より四角形$OACB = 2 \times \triangle OAC = 2 \times 8\sqrt{3} = 16\sqrt{3}$。
また、おうぎ形$OAB = \pi 4^2 \times \frac{120}{360}$である。よって斜線部分の面積は四角形$OACB$-おうぎ形$OAC = 16\sqrt{3} – \frac{16}{3}\pi$
(2)
① $\frac{3}{2}$
$x=0$のとき$y=\frac{1}{4}\times0^2=0$, $x=6$のとき$y=\frac{1}{4}\times6^2=9$より変化の割合は$\frac{9-0}{6-0}=\frac{3}{2}$
② 12
舞さんの走る時間と距離のグラフはボールのグラフの$x=0,6$の部分で交わる直線であるので、①で求めた変化の割合より、$y=\frac{3}{2}x$である。
ボールが舞さんを追い越してから舞さんとボールの間の距離が18mになるのを式で表すと$\frac{1}{4}x^2 – \frac{3}{2}x=18$となり、これを解くと$x=12, -6$となるが、ボールが舞さんを追い越した後という条件を満たすのは$x=12$のみとなるので12秒後である。
(3)およそ 1200 個
最初に箱の中にあった白玉の数を$x$個とすると、赤玉は$4x$個となる。
白玉を追加すると白玉は$(x+300)$個となるので、120個無作為抽出すると赤玉は$120 \times \frac{4x}{(x+300)+4x} = 80$個あったと考えることができる。これを解くと$x=300$となり、赤玉は$4 \times 300 = 1200$個あったと考えられる。
(4)
① 15行目の3列目
図から、数字が6つ進むごとに2行進むことに着目して、$45 \div 6 = 7$あまり3から分かる。
②
ア:$3n-2$
$n$行目の最大の数は$3n$であり、それより2だけ小さいので$P=3n-2$
イ:177
$Q=3(n-1)$より$P+Q=(3n-2)+3(n-1)=6n-5$である。問題文の$P+Q=349$より$6n-5=349$を解いて、$n=59$であり、奇数行目であるから最大の数となり、求める数は$3 \times 59 = 177$
数学の授業で、生徒たちが、直線 $y=x$ と三角形を素材にした応用問題を考えることになりました。次の(1)(2)の問いに答えなさい。
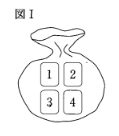
(1)京子さんと和真さんは、確率を求める問題をつくろうとしています。2人は、図Ⅰのような、1、2、3、4の数字が1つずつ書かれた4枚のカードが入った袋を使い、次の【操作】をすることを考え、それをもとに、以下のような会話をしています。あとの①、②の問いに答えなさい。
【操作】
・袋の中のカードを良くかき混ぜて、カードを1枚取り出し、カードに書かれた数を確認してからもとに戻す。この作業を2回行う。
・1回目に取り出したカードに書かれた数を$a$として、直線 $y=x$ 上に $(a, a)$ となる点Pをとる。
・2回目に取り出したカードに書かれた数をbとして、$x$軸上に $(b, 0)$ となる点Qをとる。
・原点O、点P、点Qをそれぞれ結んで、$\triangle\text{OPQ}$をつくる。
【会話文】
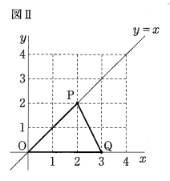
京子さん:この【操作】をすると、取り出すカードによって、さまざまな形の$\triangle\text{OPQ}$ができるね。
和真さん:たとえば、取り出したカードに書かれた数が、1回目が2で、2回目が3のときの$\triangle\text{OPQ}$は図Ⅱのようになるよ。他の場合もやってみよう。
京子さん:すべての場合をかいたけれど、この中に、合同な三角形の組はないようだね。つまり、【操作】にしたがって$\triangle\text{OPQ}$をつくるとき、$\triangle\text{OPQ}$は全部で【 ① 】通りあるね。
和真さん:$\triangle\text{OPQ}$が直角三角形になる場合があったよ。この確率を求める問題にしよう。
① 【 ① 】にあてはまる正しい数を答えなさい
② 【操作】にしたがって$\triangle\text{OPQ}$をつくるとき、$\triangle\text{OPQ}$が直角三角形になる確率を求めなさい。
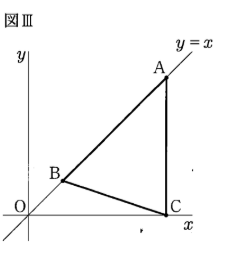
(2)優矢さんと志保さんは、三角形の面積を2等分する問題をつくろうとしています。2人は、直線 $y=x$ 上の2点 $(4, 4), (1, 1)$ をそれぞれA、B、$x$軸上の点$(4, 0)$をCとし、3点A、B、Cをそれぞれ結んで、$\triangle\text{ABC}$をつくりました。図Ⅲは、直線 $y=x$ と$\triangle\text{ABC}$をかいたものです。2人は、図IIIを見ながら、下記の会話をしています。
あとの①~③の問いに答えなさい。
【会話文】
優矢さん:頂点Aを通り、$\triangle\text{ABC}$の面積を2等分する直線は、$\triangle\text{ABC}$が二等辺三角形ではないようだから、【 ② 】だね。
志保さん:頂点を通らない直線で$\triangle\text{ABC}$の面積を2等分する場合も考えてみようよ。
優矢さん:直線 $y=x$ 上の点 $(3, 3)$ をDとして、点Dを通り、$\triangle\text{ABC}$の面積を2等分する直線だとどうなるかな。
志保さん:その直線は辺BCと交わりそうだよ。その直線と辺BCとの交点の座標を求める問題にしよう。
①【 ② 】にあてはまるものとして正しいものを、次のア~エから1つ選び、記号で答えなさい。
ア $\angle\text{BAC}$の二等分線
イ 辺BCの垂直二等分線
ウ 頂点Aから辺BCへの垂線
エ 頂点Aと辺BCの中点を通る直線
② 下線部について、2点B、Cを通る直線の式を求めなさい。
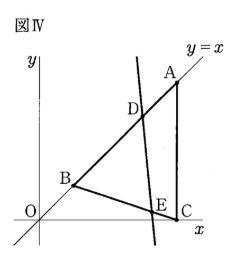
③ 図Ⅳは、優矢さんと志保さんが、図Ⅲにおいて、点Dを通り、$\angle\text{ABC}$の面積を2等分する直線を書き、その直線と辺BCとの交点をEとしたものです。
点Eの座標を求めなさい。
(1)
① 15行目の3列目
図から、数字が6つ進むごとに2行進むことに着目して、$45 \div 6 = 7$あまり3から分かる。
② $\frac{3}{8}$
$\angle PQO = 90^\circ$となるのは$a=b$のときであり、$(a,b)=(1,1), (2,2), (3,3), (4,4)$の4通りである。$\angle OPQ = 90^\circ$となるのは$b=2a$のときであり、$(a,b)=(1,2), (2,4)$の2通りである。$\angle POQ = 45^\circ$より$90^\circ$とならないので$\triangle OPQ$が直角三角形となるのは$4+2=6$通りである。よって求める確率は$\frac{6}{16}=\frac{3}{8}$
(2)
① エ
エにおいて、中点を通る直線を引くことによって底辺と高さが等しい三角形ができ、面積は等しくなる。ほかの選択肢は$AB=AC$のときのみ当てはまる。
② $y = -\frac{1}{3}x + \frac{4}{3}$
BCの中点は$(\frac{1+4}{2}, \frac{1+0}{2})=(\frac{5}{2}, \frac{1}{2})$であり、(1)よりこの点とAを通る直線を求めればよい。この直線の式を$y=ax+b$とおくと、$4=4a+b, \frac{1}{2}=\frac{5}{2}a+b$となり、この連立方程式を解いて$a=-\frac{1}{3}, b=\frac{4}{3}$となるので直線の式は$y=-\frac{1}
③ $(\frac{13}{4}, \frac{1}{4})$
$\triangle BDE = \frac{1}{2}\triangle ABC$より$\frac{BD}{AD}\times\frac{BE}{BC}=\frac{1}{2}$となればよい。
ここで$x$座標をみると、$BD:AD=(3-1):(4-1)=2:3$より$\frac{2}{3}\times\frac{BE}{BC}=\frac{1}{2}$となり、$\frac{BE}{BC}=\frac{3}{4}$である。
よってEの$x$座標は$1+(4-1)\times\frac{3}{4}=\frac{13}{4}$、$y$座標は$1+(0-1)\times\frac{3}{4}=\frac{1}{4}$
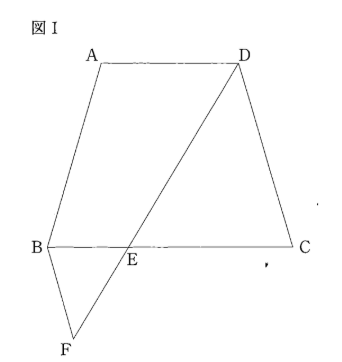
図Ⅰのような、AB=DC=7cm、AD=5cm、EC=9cm、AD//BCの台形ABCDがあります。辺BC上に、BE=3cmとなる点Eをとります。また、直線DE上に、DE:EF=2:1となる点Fを、直線BCに対して点Dと反対側に取り、点Bと点Fをむずびます。次の(1)~(3)の問いに答えなさい。
(1)$\triangle\text{CDE} \backsim \triangle\text{BFE}$であることを証明しなさい。
(2)線分BFの長さを求めなさい。
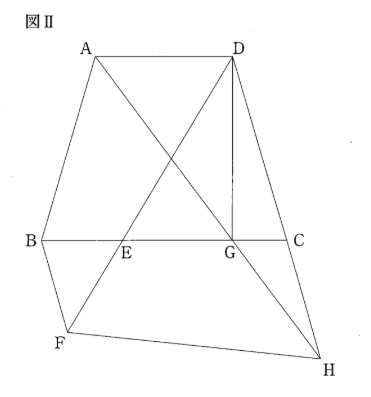
(3)図Ⅱは、図Ⅰにおいて、点Dから辺BCに垂線をひき、辺BCとの交点をGとしたものです。また、直線AGと直線DCとの交点をHとし、点Fと点Hを結びます。 次の①、②の問いに答えなさい。
① 線分DGの長さを求めなさい。
② 四角形BFHCの面積を求めなさい。
(1)
$\triangle CDE \backsim \triangle BFE$において、仮定から$BE:FE=2:1$ …①
$BC=9$ cm, $BE=3$ cm より$CE=6$ cm であるから$CE:FE=2:1$ …②
①、②より$DE:FE=CE:BE …③
対頂角は等しいから$\angle CED = \angle BEF$ …④
③、④より、2組の辺の比とその間の角がそれぞれ等しいから$\triangle CDE \backsim \triangle BFE$
問題文から2組の辺の比が読み取れるので、それを利用する。
(2)$\frac{7}{2}$ cm
(1)より$CD:BF=2:1$だから$BF=CD \times \frac{1}{2} = \frac{7}{2}$ [cm]
(3)
① $3\sqrt{5}$ cm
AからBCに垂線を下ろし、それとBCの中点をIとおくと、台形の高さは一定だから$AI=DG$で、仮定より$AB=DC$であり、垂線だから$\angle AIB = \angle DGC = 90^\circ$
これらより、直角三角形の斜辺と他の一辺がそれぞれ等しいので、$\triangle AIB \equiv \triangle DGC$
よって$BI=CG$であるから$BC=BI+IG+GC=2GC+AD$、$GC=\frac{BC-AD}{2}=\frac{9-5}{2}=2$[cm]である。
$\angle DGC = 90^\circ$より、$DG=\sqrt{CD^2-GC^2}=\sqrt{7^2-2^2}=\sqrt{45}=3\sqrt{5}$
②$\frac{63\sqrt{5}}{4}$ cm$^2$
BからCDにおろした垂線とCDの交点をJとおくと、$\angle DGC = \angle BJC = 90^\circ$, $\angle C$共通より、2組の角がそれぞれ等しいので、$\triangle DGC \backsim \triangle BJC$であるから$CD:CB=DG:BJ$
よって$BJ=DG \times \frac{CB}{CD} = 3\sqrt{5} \times \frac{9}{7} = \frac{27\sqrt{5}}{7}$[cm]である。
また、$AD//GC$より、同位角を考えると$\angle DAH = \angle CGH$, $\angle ADH = \angle GCH$だから2組の角がそれぞれ等しいので$\triangle ADH \backsim \triangle GCH$
よって$DH:CH=AD:GC=5:2$、$CH=CD \times \frac{2}{7} = 2$[cm]である。
四角形BFHCは$BF//CH$の台形で、$BJ$はその高さになるから、
求める面積は$(BF+CH) \times BJ \times \frac{1}{2} = (\frac{7}{2}+2) \times \frac{27\sqrt{5}}{7} \times \frac{1}{2} = \frac{63\sqrt{5}}{4}$[cm$^2$]
家庭教師のやる気アシストは、宮城県にお住まいの受験生のお子さんを毎年たくさん指導をさせ頂き、合格に導いています。
高い合格率の秘訣は、指導経験豊富な先生の指導力に加え、1対1の指導でお子さん一人ひとりの状況に合わせた、お子さんだけのカリキュラムで勉強が進められるから!
家庭教師のやる気アシストは、お子さんの志望校合格まで全力でサポートさせて頂きます!
お子さんにとって「成果が出る勉強法」ってどんな勉強法だと思いますか?
お子さんそれぞれに、個性や性格、学力の差もあります。そんな十人十色のお子さん全員に合う勉強法ってなかなかないんです。
たからこそ、受験生の今だけでもお子さんだけの勉強法で受験を乗り越えてみませんか?
やる気アシストには、決まったカリキュラムはありません。お子さんの希望や学力、得意や不得意に合わせて、お子さんだけのカリキュラムで指導を行っていきます。また、勉強法もお子さんそれぞれに合う合わないがあります。無料体験授業では、お子さんの性格や生活スタイルを見せていただき、お子さんにとって効率的な成果の出る勉強のやり方をご提案させて頂きます。

