






奈良県の2022年3月実施の令和4年度(2022年度)入学者の公立高校入試問題の解説をしています。
受験勉強において、過去問を解くことはとても効果的な勉強法です。ぜひ、受験までに一度挑戦し、問題の傾向を掴んでおきましょう。合わせて、対策などをたてられるととても良いですね。
また、過去問で苦手な点が見つかった場合は、そこを中心に試験日当日までにしっかりと対策しておきましょう。
奈良県の数学は4つの大問で構成され、そのうち1つが小問集合となっています。その他の大問は、関数・図形が出てくることが多く空間図形はあまりテーマになることはありません。
難易度は標準といったところです。数学が得意なお子さんであれば満点を狙えると思います。
【奈良県】令和4年度一般入学者選抜の過去問はこちらから
数学の過去問題はこちら>>
次の各問い答えよ。
(1)次の①~④の計算せよ。
① 3-7
② 4(x+2)+2(x-3)
③ 12xy²÷4x²×3xy
④ (x+2)(x+8)ー(x+4)(xー4)
(2)2次方程式 x²-6x+2=0 を解け。
(3)x=√2+3 のとき, x²-6x+9 の値を求めよ。
(4)yはxの2乗に比例し,x=2のときy=-8である。yをxの式で表せ。
(5)右の表は、ある学級の生徒40人の通学時間を度数分布表に整理したものである。
中央値(メジアン)が含まれる階級の相対度数を求めよ。

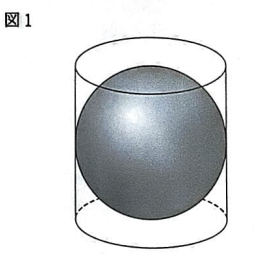
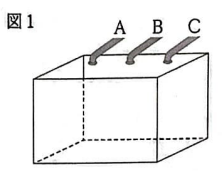
(6)図1のように、底面の直径と高さが等しい円柱の中に、直径が円柱の高さと等しい球が入っている。このとき、球の体積は円柱の体積がの何倍か。
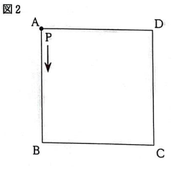
(7)図2のようにな正方形ABCDがあり、点Pが頂点Aの位置にある。
2つのさいころを同時に1回投げて、出た目の数の和を同じ数だけ、点Pは頂点B、C、D、A、B、…の順に各頂点を反対時計回りに1つずつ移動する。例えば、2つのさいころの出た目の数の和が5のとき、点Pは頂点Bの位置に移動する。
2つのさいころを同時に1回投げたとき、点Pが頂点Dの位置に移動する確率を求めよ。
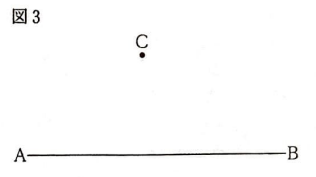
(8)図3のように線分ABと点Cがある。線分AB上にあり、∠APC=45°となる点Pを、定規をコンパスをつって解答欄の枠内に作図せよ。なお、作図に使った線は消さずに残しておくこと。
(1)① 【正答 -4】
(1)② 【正答 6x+2】
=4x+8+2x-6
=6x+2
(1)③ 【正答 9xy²】
(1)④ 【正答 10x+32】
=x²+10x+16-x²+16
=10x+32
(2) 【正答 x=3±√7】
二次方程式の解の公式に代入して、
x=[-(-6)±√{(-6)²-4×1×2}]/ (2×1)
=(6±√28) / 2
=3±√7
(3) 【正答 2】
=(√2+3)²-6(√2+3)+9
=2+6√2+9ー6√2-18+9
=2
(4) 【正答 y=-2x²】
yはxの2乗に比例するので、求める式の形は y=ax² ー①となる。
①にx=2、y=-8を代入して、
-8=a×2²
a=-2
よって、 y=-2x²
(5) 【正答 0.15】
全体で40人いるので、中央値は20と21番目の間の数値となる。
中央値は20~25の階級に含まれる。この階級の相対度数は、
6÷40=0.15
(6) 【正答 2/3 倍】
円柱の底面の半径をaとおく。底面の直径と高さが等しいので、円柱の高さは2a
よって、この円柱の体積は、
a²×π×2a=2πa³ ー①
また、球の直径は円柱の高さと等しいので、球の半径はaと表せる。
よって、球の体積は、
4/3×π×a³=4πa³/3 ー②
①、②より、
2πa³÷4πa³/3=2/3
(7) 【正答 5/18】
頂点Dの位置に移動するには、サイコロの目の和が3、7、11のいずれかになる必要がある。
サイコロの目の出方は、6×6=36通り
3になる組み合わせは、(1、2)、(2、1) の2通り。
7になる組み合わせは、(1、6)、(2、5)、(3、4) 、(4、3) 、(5、2) 、(6、1) の6通り。
11になる組み合わせは、(5、6)、(6、5) の2通り。
よって、求める確率は、
(2+6+2)/36=10/36=5/18
(8) 【正答】
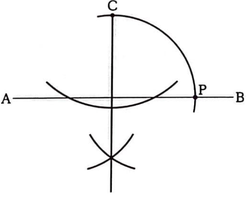
図1のように、深さ50㎝の直応対の容器と給水管A、B、Cがある。この容器が空の状態から、給水管を使って6分間水を入れる。
この容器では、給水管A、B、Cを使うと、それぞれ毎分12㎝、毎分6㎝、毎分2㎝の割合で水面が高くなる。ただし、給水管は同時に複数使わないものとする。各問いに答えよ。
① 【(あ)】に当てはまる式を書け。
② 【(い)】、【(う)】に当てはまる語句の組み合わせを、次のア~エから1る選び、その記号を書け。
ア 【(い)】水面が1㎝高くなるのにかかる時間 【(う)】給水管Aの使用時間
イ 【(い)】水面が1㎝高くなるのにかかる時間 【(う)】給水管Bの使用時間
ウ 【(い)】1分あたりに高くなる水面の高さ 【(う)】給水管Aの使用時間
エ 【(い)】1分あたりに高くなる水面の高さ 【(う)】給水管Bの使用時間
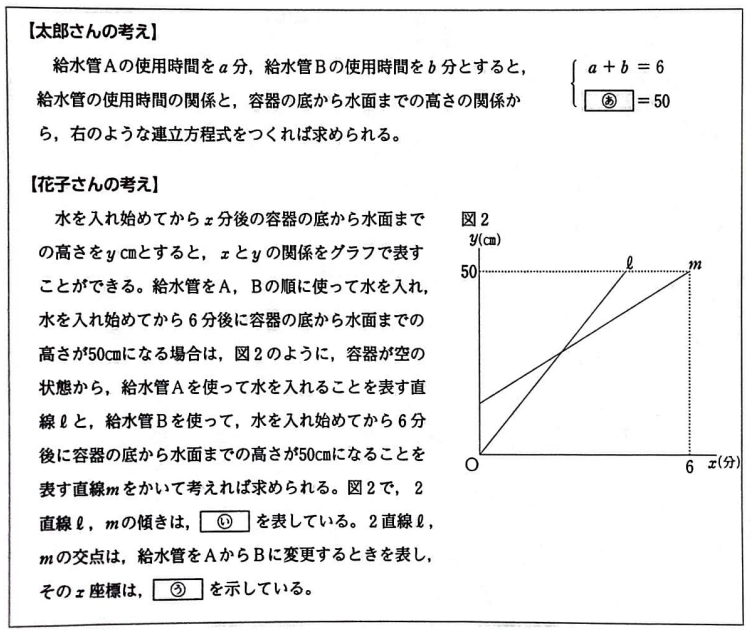
(2)給水管をA、Bの順、またはA、Cの順に使って水を入れる。次の▭内は、水を入れ始めてから6分後に容器の底から水面までの高さが45㎝になる場合について、図2をもとに考えた太郎さんと花子さんの会話である。①、②の問いに答えよ。
太郎:容器の底から水面までの高さを50㎝から45㎝に変更して水を入れる場合、グラフを使って考えると、どうすればいいか。
花子:給水管をA、Bの順に使って水を入れ、水を入れ始めてから6分後に容器の底から水面までの高さが45㎝なることを考えるには、図2に、(え)直線を1本かき加えるといいよ。
太郎:直線1本書き加えることで、視覚的に考えることができるね。次に、給水管をA、Cの順に使って水を入れた場合、グラフを使って考えると、どうすればいいのかな。
花子:給水管A、Bの順に使う場合で考えたときにと同じように、給水管をA、Cの順に使って水を入れ、水を入れ始めてから6分後に容器の底から水面までの高さが45㎝になることを考えるには、図2に、(お)直線を1本書き加えるといいよ。
① 下線部(え)はどのような直線か。「直線m」の語を用いて簡潔に説明せよ。
② 次のア~エの中に、下線部(お)を適切に表しているグラフが1つある。そのグラフを、ア~エから1つ選び、その記号を書け。
なお、——-線は、図2の直線l、mを示している。
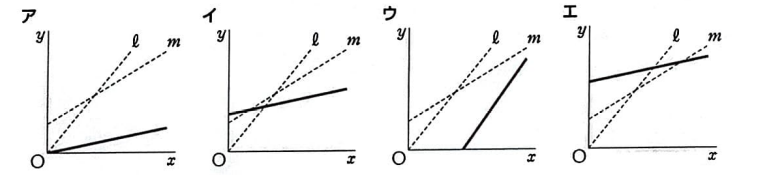
図1のように、深さ50㎝の直応対の容器と給水管A、B、Cがある。この容器が空の状態から、給水管を使って6分間水を入れる。
この容器では、給水管A、B、Cを使うと、それぞれ毎分12㎝、毎分6㎝、毎分2㎝の割合で水面が高くなる。ただし、給水管は同時に複数使わないものとする。各問いに答えよ。
(1)給水管をA、Bの順位使って水を入れる。次の▭内は、水を入れ始めてから6分後に容器の底から水面までの高さが50㎝になる場合の給水管A、Bの使用時間の求め方について、太郎さんと花子さんがそれぞれ考えたものである。①、②の問いに答えよ。
(1)① 【正答 12a+6b】
(1)② 【正答 ウ】
傾きは、(yの増加量)/(xの増加量)で求めることができる。
(2)① 【正答 (例)直線mをy軸の負の方向に5だけ平行移動した直線】
(1)の問題文の▭の花子さんの考えに従って、直線を引く。
容器の高さが、50㎝から5㎝だけ低くなっているので、書き加える直線も5だけ下げる。
(2)② 【正答 エ】
水を入れ始めてから、6分後に45㎝になるように線をかき足す。
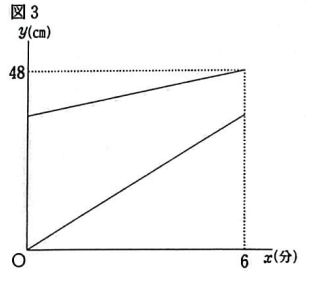
(3) 【正答 4分12秒後】
給水管Bを用いて、水を1分間加えると、6㎝ためることができる。
給水管A、Cを用いて、5分間で残り42㎝水をためることを考えればよい。
(1)の問題文の▭の太郎さんの考えを使い求める。
給水管Aの使用時間をa分、給水管Cの使用時間をc分とすると、
a+c=5
12a+2c=42
これを解くと、a=3.2分=3分12秒
給水管Bを入れ始めから、給水管をCに変更するまでの時間なので、
1分+3分12秒=4分12秒
図で、曲線は関数 y=6/x のグラフである。2点A、Bの座標はそれぞれ(-6、-1)、(-3、-5)である。点Cは、曲線上を動く点であり、点Dはx軸上を動く点である。2点C、Dのx座標はどちらも正の数である。原点をOとして、各問いに答えよ。
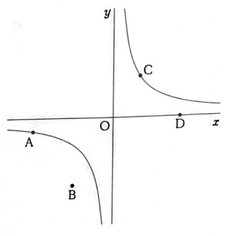
(1)点Cのx座標が1であるとき、点Cのy座標を求めよ。
(2)2点C、Dが、OC=CDを保ちながら動くとき、点Cのx座標が大きくなるにつれて、△OCDの面積の値はどのようになるか。次のア~オのうち、正しいものを1つ選び、その記号を書け。
ア 大きくなる。 イ 大きくなってから小さくなる。
ウ 小さくなる。 エ 小さくなってから大きくなる。
オ 一定である。
(3)△OABの面積を△OBDの面積が等しくなるように点Dをとるとき、点Dのx座標を求めよ。
(4)四角形ABCDが平行四辺形になるように2点C、Dをとるとき、2点B、Dを通る直線の式を求めよ。
(1) 【正答 6】
y=6/xにx=1を代入すればいいので、
y=6
(2) 【正答 オ】
点Cの座標は、(x,6/x)
OC=CDより、△OCDは常に二等辺三角形になるので、
点Dの座標は、(2x,0)
よって、△OCDの面積は、
2x×6/x×1/2=6
面積の値は常に一定になる。
(3)①【正答 27/5】
まず、△OABの面積を求める。
y軸と平行で点Aに接するような線lをひく。
x軸と平行で点Bに接するような線mをひく。
直線lとx軸が交わる点をE、直線lと直線mが交わる点をF、直線mとy軸が交わる点をGとする。
それぞれの座標は、
E(-6,0)、F(-6,-5)、G(0,-5)
となる。
△OAB=四角形OEFG-△OEA-△ABF-△OBG
={|−6|×|−5|}-{|−6|×|−1|×1/2}-{|(−5-(−1))|×|(−6-(−3))|×1/2}-{|−3|×|−5|×1/2}
=30-3-6-15/2
=27/2
点Dの座標を(a,0)とおく。
△OBDの面積をaを使って表すと、
a×|−6|×1/2
これが、27/2と等しいので、
27/2=a×|−5|×1/2
a=27/5
(3)② 【正答 y=2x/3-3】
線分ABの傾きは、
(-6、-1)、(-3、-5)
x軸方向の増加量は|(−6)-(−3)|=3 ー①
y軸方向の増加量は|(−1)-(−5)|=4 ー②
四角形ABCDは平行四辺形なので、
線分CDも同じような増加量になる。
C、Dの座標をそれぞれ
C(t,6/t)、D(s,0)とおくと、①、②より
(ただし、t>0、s>0、t>s)
|t-s|=3
|6/t-0|=4
⇔t=3/2
s=9/2
よって、BDをとおる直線の式は
直線の式に、B(-3、-5)、D(9/2、0)を代入して
-5=-3a+b
0=9/2a+b
この2つの連立方程式を解いて、
a=2/3
b=-3
求める直線は
y=2x/3-3
図のように、円周上に4点A、B、C、Dがあり、AB=ADである。
線分ACと線分BDとの交点をEとする。また、点Aを通り線分BCと平行な直線と、線分BD、線分CDとの交点をそれぞれF、Gとする。各問いに答えよ。
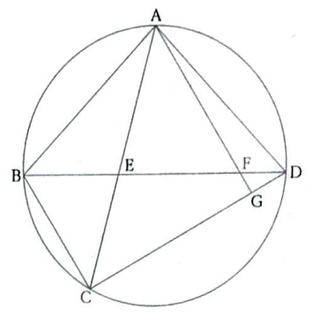
(1)∠ABD=a°とするとき、∠BCDの大きさをaを用いて表せ。
(2)△AEF∽△CEBを証明せよ。
(3)AB=6㎝、BC=4㎝、AC=8㎝のとき、①、②の問いに答えよ。
①△ABEの面積は△BCEの面積は何倍か。
②線分AGの長さを求めよ。
(1) 【正答 2a°】
△ABDはAB=ADの二等辺三角形なので、
∠ABD=∠ADB=a
また、同じ弧に対する円周角は等しいので、
∠ABD=∠ACD(=a) ー①
∠ADB=∠ACB(=a) ー②
①、②より、
∠BCD=∠ACD+∠ACB
=2a
(2) 【正答 (例)
△AEFと△CEBにおいて
平行線の錯角は等しいから、AG//BCより
∠EAF=∠ECB ー①
対頂角は等しいから
∠AEF=∠CEB -②
①、②より
2組の角がそれぞれ等しいから
△AEF∽△CEB 】
(3)① 【正答 9/7】
△ABCと△AEBにおいて、
(1)より、
∠ABD=∠ACB
∠BAC=∠EAB
なので、 △ABC∽△AEB
AC:AB=4:3より、
△ABC:△AEB=4:3
面積比は相似比の2乗なので、
△ABC:△AEB=16:9
△BCE=△ABC-△AEB=7
よって△BCE、△AEBの面積比は
△BCE:△AEB=7:9
よって、9/7倍
(3)② 【正答 64/11】
全ての角が等しいので、
△BCE∽△ADE
BC:AD=4:6より、
△BCE、△ADEの面積比は
△BCE:△ADE=4:9
より、△ADE=7×9/4=63/4
また、
AE:EC=9:7
より、
△ABE:△BCE=AE:EC=△ADE:△CDE=9:7
△CDE=63/4×9/7=49/4
△BCD:△ADC=7+49/4:63/4+49/4
=112/4:77/4
=16:11
よって、
AGの長さは
4×16/11=64/11
家庭教師のやる気アシストは、奈良県にお住まいの受験生のお子さんを毎年たくさん指導をさせ頂き、合格に導いています。
おかげさまで、昨年度の合格率は、関西エリア全体で97.3%という結果を残すことが出来ました。
高い合格率の秘訣は、指導経験豊富な先生の指導力に加え、1対1の指導でお子さん一人ひとりの状況に合わせた、お子さんだけのカリキュラムで勉強が進められるから!
家庭教師のやる気アシストは、お子さんの志望校合格まで全力でサポートさせて頂きます!
お子さんにとって「成果が出る勉強法」ってどんな勉強法だと思いますか?
お子さんそれぞれに、個性や性格、学力の差もあります。そんな十人十色のお子さん全員に合う勉強法ってなかなかないんです。
たからこそ、受験生の今だけでもお子さんだけの勉強法で受験を乗り越えてみませんか?
やる気アシストには、決まったカリキュラムはありません。お子さんの希望や学力、得意や不得意に合わせて、お子さんだけのカリキュラムで指導を行っていきます。また、勉強法もお子さんそれぞれに合う合わないがあります。無料体験授業では、お子さんの性格や生活スタイルを見せていただき、お子さんにとって効率的な成果の出る勉強のやり方をご提案させて頂きます。

