【奈良県】令和6年度/2024年度入学者高校入試選抜試験：数学の解説
奈良県の2024年3月実施の令和6年度（2024年度）入学者の公立高校入試問題の解説をしています。
受験勉強において、過去問を解くことはとても効果的な勉強法です。ぜひ、受験までに一度挑戦し、問題の傾向を掴んでおきましょう。
合わせて、対策などをたてられるととても良いですね。
また、過去問で苦手な点が見つかった場合は、そこを中心に試験日当日までにしっかりと対策しておきましょう。
大問1
問題文
次の各問いに答えよ。
(1) 次の①～④を計算せよ。
① －3－（－7）
② 3(2x－1)＋x－4
③ 10xy² ÷ 5y × 2x
④ (x＋4)(x－4)－(x－3)³
(2) 二次方程式を解け。 x²＋x－5＝0
(3) 「1本x円の鉛筆3本と1冊y円のノート5冊の代金の合計は、500円より高い」という数量の関係を不等式で表せ。
(4) yはxに反比例し、x＝－6のときy＝4である。ｙ＝3のときのｘの値を求めよ。
(5) 二つのさいころA、Bを同時に投げるとき、Aのさいころの出る目の数がBのさいころの出る目の数より大きくなる確率を求めよ。
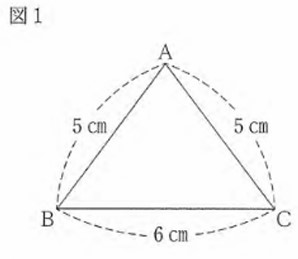
(6) 図1で、△ABC は AB=AC=5㎝ 、BC=6㎝ の二等辺三角形である。この二等辺三角形を、辺BCを軸として1回転させてできる立体の体積を求めよ。ただし、円周率はπとする。
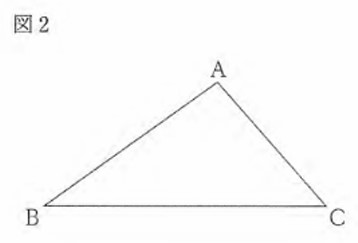
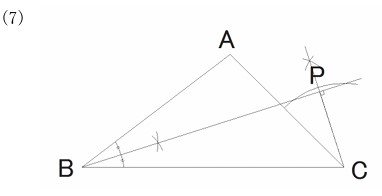
(7) 図2のように、△ABC がある。次の条件①、②を満たす点Pを、定規とコンパスを使って作図せよ。なお、作図に使った線は消さずに残しておくこと。
〔条件〕
① ∠ABP =∠CBPである。
② BP⊥CPである。
(8) 太郎さんと花子さんは, A中学校の図書委員である。 ①、②の問いに答えよ。
① 太郎さんと花子さんは、 3年1組の生徒36人と3年2組の生徒37人が1学期に読んだ本の冊数を調べた。図3は、その結果をそれぞれ箱ひげ図に表したものである。 図3の2つの箱ひげ図から読み取ることができることがらとして適切なものを、後のア～エから全て選び、その記号を書け。
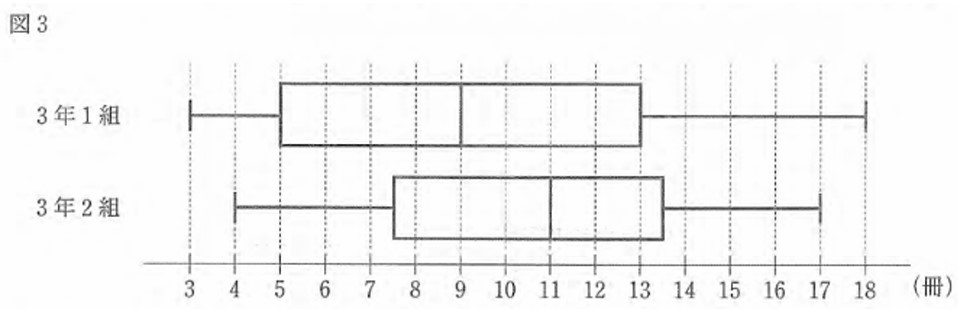
ア 読んだ本の冊数の範囲は、1組よりも2組の方が大きい。
イ 1組で、読んだ本の冊数の第1四分位数は、5冊である。
ウ 2組で読んだ本の冊数が14冊以上である生徒は、 9人いる。
エ 1組、 2組ともに、読んだ本の冊数が13冊である生徒は、 少なくとも1人はいる。
② 次の□内は、A中学校の全校生徒240人が1学期に読んだ本の冊数の平均について考えた、花子さんと太郎さんの会話である。 ［ ］のように言える理由を簡潔に書け。
花子 : 1学期に読んだ本の冊数の平均を調べるために、全校生徒240人を母集団とする標本調査をしたいね。
太郎 : 3年1組の生徒を標本として選ぶのはどうかな。 3年1組の生徒36人が1学期に読んだ本の冊数の平均は9.6冊だったよ。
花子 : ［その標本の取り出し方は適切ではないよ。］
解答・解説
(5) Aの目が1の時Bの目よりも大きくなるのは0通り
Aの目が2の時Bの目よりも大きくなるのは1通り
Aの目が3の時Bの目よりも大きくなるのは2通り
…と考えると条件を満たすのは全部で15通り
よって求める確率は、15/36＝5/12
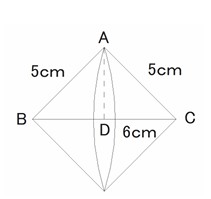
(6) △ABCを回転させると右図のような円錐を2つ合わせた立体になる。
BCの中点をDとすると、△ABDにおいて三平方の定理よりAB²=AD²+BD²
5²= AD²+3² より、AD=4
よって、求める面積は、AD²× ×BD×1/3×2 π=16× ×3×1/3×2 π
=32 cm³
(8)① イ、ウ
ア、読んだ本の冊数の範囲は、1組よりも2組の方が大きい 。→小さい
イ、1組で、読んだ本の冊数の第1四分位数は5冊である。→〇
ウ、2組で読んだ本の冊数が14冊以上である生徒は9人いる。→〇（37÷4>9であるから、14冊〜17冊は9人いることが分かる）
エ、1組、2組ともに、読んだ本の冊数が13冊である生徒は少なくとも1人はいる→×
② 3年1組だけでは学年も1学年であり、無作為に抽出したとはいえないから。
大問2
問題文
写真1のように、 箱詰めされた缶ジュースが40本ある。太郎さんと花子さんは、 写真2のように詰め替えると、缶ジュースが41本入ったことから、箱の中にどのように缶ジュースを詰めるかで、入る本数が変わることに興味をもった。 図1、 2はそれぞれ写真1、 2をもとに、 箱を長方形ABCD、 缶を円として表した図である。AB=10cm、 AD=16cm、円の半径を1cmとして、各問いに答えよ。
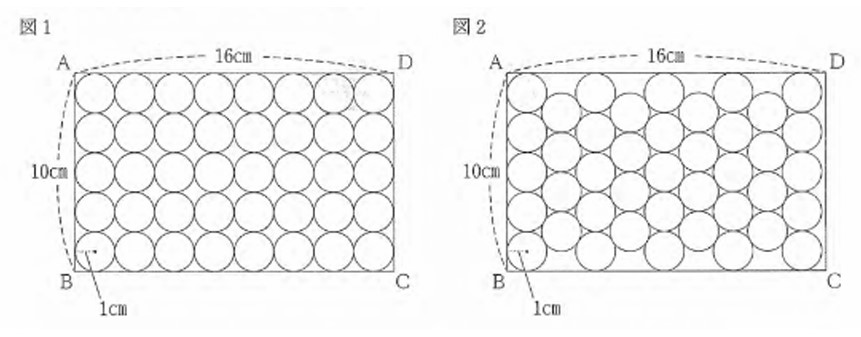
(1) 次の□内は、図1、 2を見て考えた、花子さんと太郎さんの会話である。 ①、②の問いに答えよ。
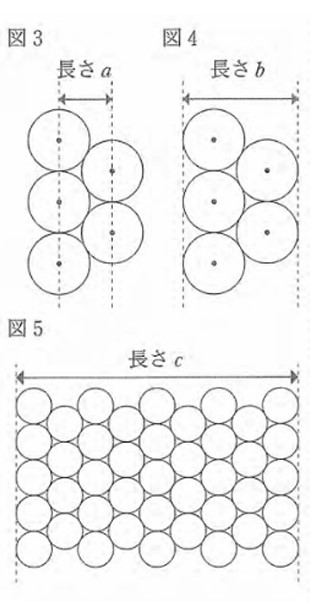
① あ・い・う に当てはまる数を、それぞれ書け。
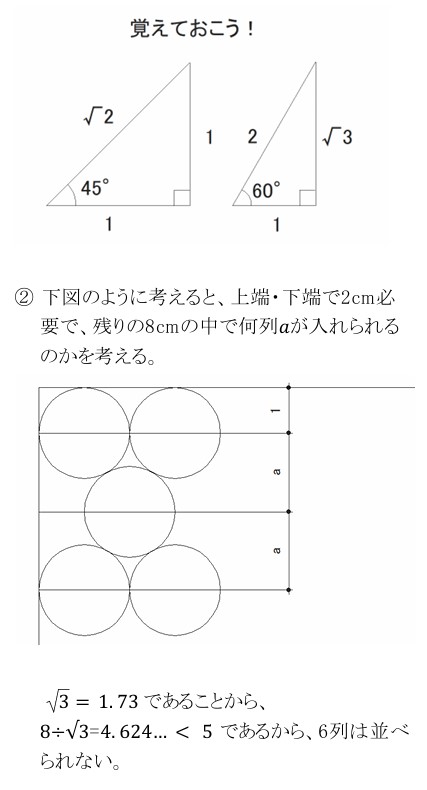
次の 【太郎さんの考え】 が正しいか正しくないかを、根拠を示して説明せよ。 ただし, √3＝1.73とする。
【太郎さんの考え 】
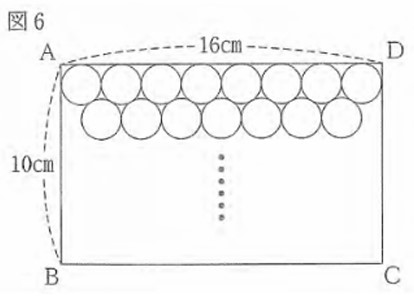
図2のように並べると、図2のほうが図1より、1列多く並べられたので、図6のように、上から 横に8個、横に7個、･･････と交互に並べると、長方形ABCD内に上から6列並べられるはずだ。
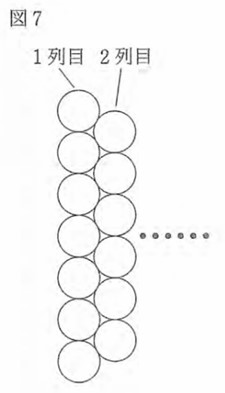
(2) 太郎さんと花子さんは、図7のように、円を左から縦に7個、縦に6個、････と交互にｎ列目まで並べていくときの、円の個数について考えた。 1列目からｎ列目まで並べた円の個数を、ｎが偶数のときと、ｎが奇数のときについて、それぞれをｎを用いた式で表せ。
解答・解説
(1) ① あ、√3 い、2+ √3 う、 2＋8 √3
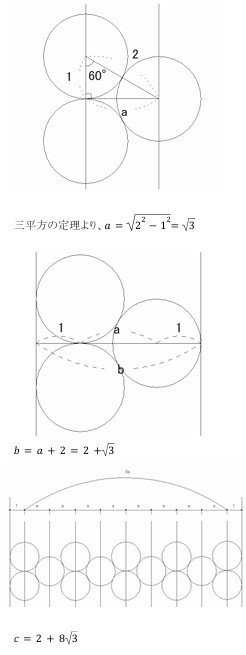
(2) 図7から、2列で合計13個並べられることがわかるので、
nが偶数の場合、n/2×13= 13n/2
nが奇数の場合、(n-1)/2 × 13 + 7 = 13n/2 + 1/2
大問3
問題文
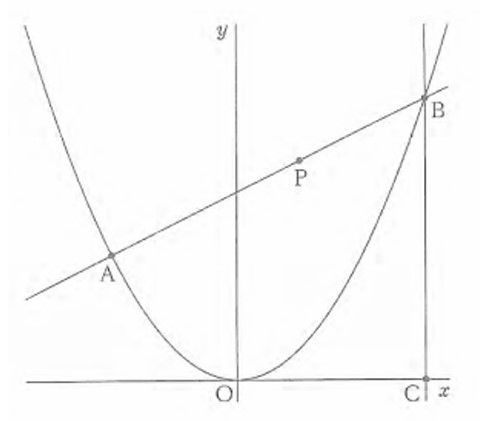
上の図で、放物線は関数ｙ＝1/4ｘ²のグラフである。 点A,Bは放物線上の点であり,その ｘ座標はそれぞれ-4, 6である。 点Cは点Bを通り ｙ軸に平行な直線とｘ軸との交点であり、点Pは線分AB上を点Aから点Bまで動く点である。原点をOとして,各問いに答えよ。
(1) 関数ｙ＝1/4ｘ²について、 の変域が-4≦ｘ≦6のとき、ｙの変域を求めよ。
(2) 点Pが線分AB上を点Aから点Bまで動くと、① 、②の値はどのように変化するか。 正しいものを、 それぞれア～オから1つずつ選び、その記号を書け。
①∠OCPの大きさ
ア 大きくなる。 イ 小さくなる。 ウ 一定である。エ 大きくなってから小さくなる。 オ 小さくなってから大きくなる。
②線分OPの長さ
ア 大きくなる。 イ 小さくなる。 ウ 一定である。エ 大きくなってから小さくなる。 オ 小さくなってから大きくなる。
(3) △BCPの面積が21のとき、点Pのｘ座標を求めよ。
(4) 線分OA上に点D, 線分OB上に点EをAB//DEになるようにとる。△ODEの面積が△OABの面積の である 1/16とき、直線DEの式を求めよ。
解答・解説
(1) 図より、x＝0で最小、x＝6で最大をとることがわかる。y＝x²/4 にそれぞれを代入すると(x, y)＝(0,0)(6,9)であるから求める変域は、0≦y≦9
(2) ①ア ②オ
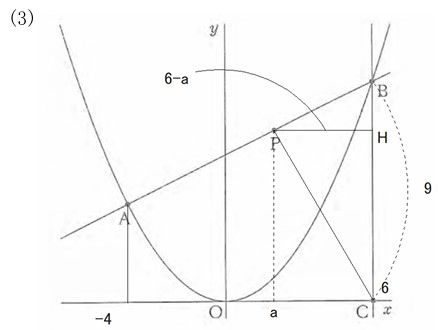
点Pのx座標をaとすると、△BCPの面積が21になるので、上図よりBC×PH÷2=9×(6−a)×1/2=21 よって、a=4/3
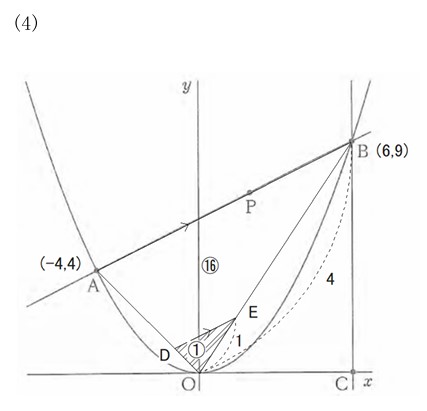
AB // DEより、△ODE∽△OABまた、その面積比が1：16であることから相似比は1：4よって、OE：OB=1：4であるから、
点Eのｘ座標は、6×1 /4 = 3/2 y座標は、9×1 /4 = 9/2
点A、Bの座標から傾きを求めると、9-4 / 6-(-4) = 5/10 = 1/2
よって、傾きが 1/2 で点Eを通ることから、y = x / 2+b に( 3/2 , 9/4 )を代入すると、9/4 = 3/2 × 1 / 2+b
b = 3/2
よって、求める式は、ｙ= 1/2 x + 3/2
0120-740-100
LINE問合せ窓口
LINEからもお問合せいただけます！
公式Instagram
勉強のお役立ち情報を配信中！
お問い合わせ、ご質問も受付中です！
ご質問などお気軽にお問い合わせください。
大問4
問題文
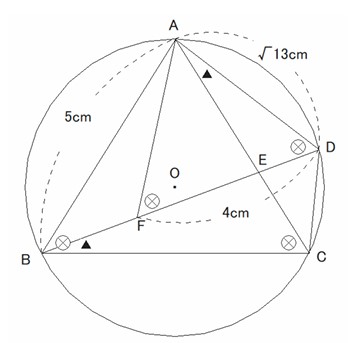
右の図で、 4点A、B、C、 Dは円Oの周上にあり、AB=ACである。 点Eは線分BDと線分ACとの交点である。 点Fは線分BD上にあり、CD=BFである。各問いに答えよ。
(1) △ABF ≡ △ACDを証明せよ。
(2) ∠BAC = a ° とするとき、∠ACBの大きさを a を用いて表せ。
(3) AB=5cm、 BD = 6cm、CD = 2cmのとき、①、②の問いに答えよ。
① 線分ADの長さを求めよ。
② △ABFの面積はAEDの面積の何倍か。
解答・解説
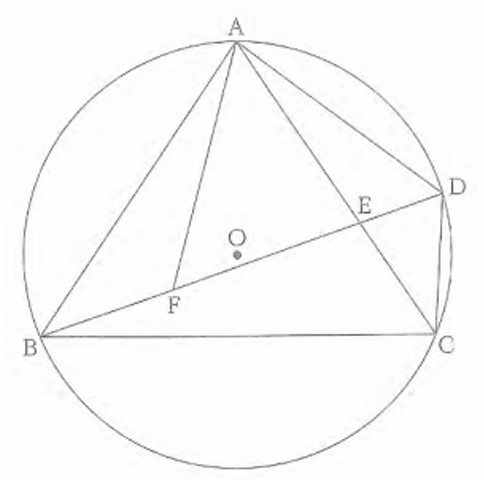
(1) △ABFと△ACDにおいて
仮定から
AB＝AC･･･①
BF＝CD･･･②
１つの弧に対する円周角は等しいから
∠ABF＝∠ACD･･･③
①,②,③より2組の辺とその間の角がそれぞれ等しいから
△ABF ≡ △ACD
(2) AB=ACであるから円周角の定理より、
∠ABC=∠ACBであるから、
∠ACB=(180°- a)÷2= 90° -a / 2
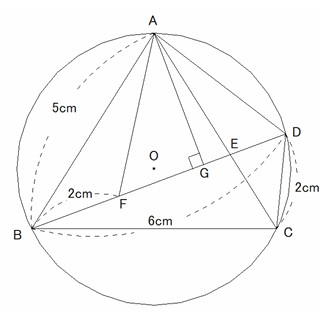
① 点AからBDにおろした垂線とBDとの交点をGとすると
AF=ADより△AFDは二等辺三角形で、FG=GDとなりBD=6,BF=2より、
FG+GD=4 から、FG=GD=2
△ABGにおいて、三平方の定理より、AB²=AG²+BG²
5²=AG²+4² よって、AG=3
△AGDにおいて、三平方の定理より、AD²=AG²+GD²=3²+2²
よって、AD= √13
② 弧ABにおいて円周角の定理から、∠ADB=∠ACB
また、AD=AFより、∠ADB=∠AFD AB=ACより、∠ABC=∠ACB
よって、2組の角が等しいことから、
△ABC∽△AFD
相似比は、AB：AF= AB：AD= 5： √13
したがって、BC：FD＝BC：4＝ 5： √13
よって、BC=20 / √13
さらに、弧CDにおいて円周角の定理から、∠CAD=∠DBC
前述から∠ADB=∠ACBなので、2組の角が等しいことから、△ADE∽△BCE
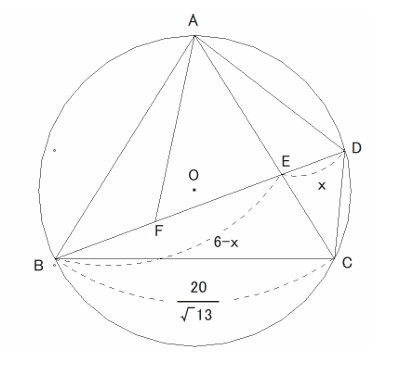
ED＝ｘとすると、BE=6-ｘであり、
AD：BC＝AE：BE
√13：20/√13＝AE：(6 -ｘ)
よって、AE＝(39/10) – (13ｘ/20)
ED：EC＝AD：BC
x：5 – AE ＝√13：20/√13
x：5 -( 39/10 – 13x/20 )＝√13：20/√13
これを解くと、x = 26 / 21
よって、△ABF：△AED＝BF：ED＝2：26/21 より、
答えは21/13倍
志望校に合わせた受験対策なら、やる気アシストにお任せ下さい！
家庭教師のやる気アシストは、奈良県にお住まいの受験生のお子さんを毎年たくさん指導をさせ頂き、合格に導いています。
高い合格率の秘訣は、指導経験豊富な先生の指導力に加え、1対1の指導でお子さん一人ひとりの状況に合わせた、お子さんだけのカリキュラムで勉強が進められるから！
家庭教師のやる気アシストは、お子さんの志望校合格まで全力でサポートさせて頂きます！
LINE問合せ窓口
LINEからもお問合せいただけます！
公式Instagram
勉強のお役立ち情報を配信中！
お問い合わせ、ご質問も受付中です！
ご質問などお気軽にお問い合わせください。
アシストの指導方法がじっくり見れる！知れる！無料の体験授業実施中
お子さんにとって「成果が出る勉強法」ってどんな勉強法だと思いますか？
お子さんそれぞれに、個性や性格、学力の差もあります。そんな十人十色のお子さん全員に合う勉強法ってなかなかないんです。
たからこそ、受験生の今だけでもお子さんだけの勉強法で受験を乗り越えてみませんか？
やる気アシストには、決まったカリキュラムはありません。お子さんの希望や学力、得意や不得意に合わせて、お子さんだけのカリキュラムで指導を行っていきます。また、勉強法もお子さんそれぞれに合う合わないがあります。無料体験授業では、お子さんの性格や生活スタイルを見せていただき、お子さんにとって効率的な成果の出る勉強のやり方をご提案させて頂きます。
