






岡山県の2022年3月実施の令和4年度(2022年度)入学者の公立高校入試問題の解説をしています。
受験勉強において、過去問を解くことはとても効果的な勉強法です。ぜひ、受験までに一度挑戦し、問題の傾向を掴んでおきましょう。合わせて、対策などをたてられるととても良いですね。
また、過去問で苦手な点が見つかった場合は、そこを中心に試験日当日までにしっかりと対策しておきましょう。
今年の岡山県の数学は6つの大問で構成され、小問集合、方程式、関数、、資料の活用、図形となっています。
難易度はやや易です。数学が得意なお子さんは満点が狙えると思います。
特に小問集合と方程式の分野が簡単です。また、関数や資料の活用は最終問題までは解けるようにしておきましょう。
図形問題は一番難易度が高いです。ただ、しっかりと見ていけば同じく最終問題までは解けると思います。
次の①~⑤の計算をしなさい。⑥~⑩は指示に従って答えなさい。
① 2-(-4)
② (-56)÷7-3
③ 2(3a-b)-(a-5b)
④ 14ab×b/2
⑤ (1+√3)²
⑥ ax²-16aを因数分解しなさい。
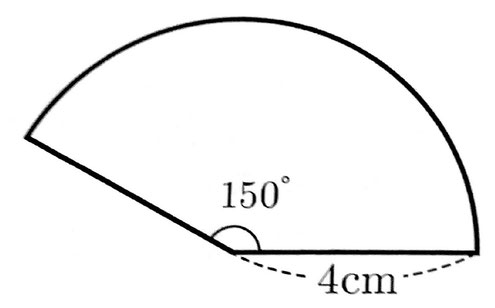
⑦ 図のような、半径4cm、中心角150°のおうぎ形があります。このおうぎ形の面積を求めなさい。
⑧ 次の方程式について、そのグラフが点(1,-2)を通るものは、ア~エのうちではどれですか。当てはまるものをすべて答えなさい。
ア 3x-y-1=0
イ 3x+2y+1=0
ウ 3y+6=0
エ x+1=0
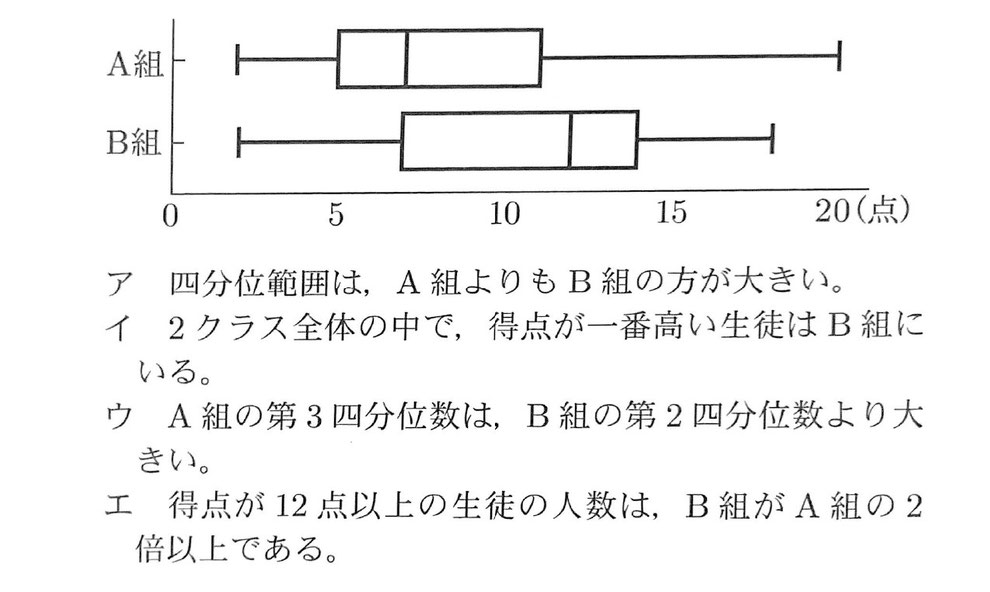
⑨ ある中学校のA組40人とB組40人の生徒が、20点満点のクイズに挑戦しました。次の箱ひげ図は、そのときの2クラス40人ずつの得点の分布を表したものです。この箱ひげ図から読み取れることを正しく説明しているのは、ア~エのうちではどれですか。当てはまるものをすべて答えなさい。
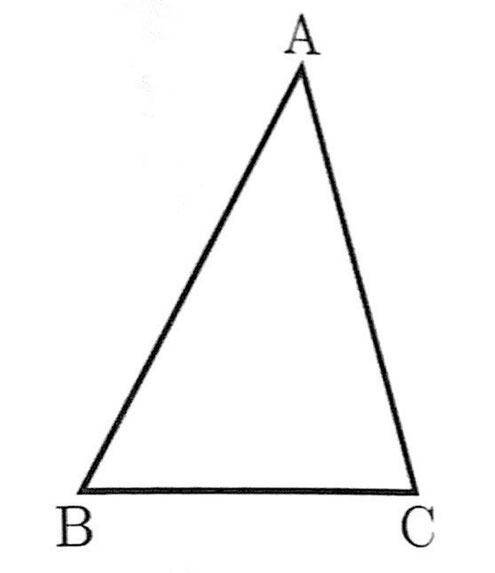
⑩ 図のような△ABCがあります。次の【条件】をすべて満たす点Pを、定規とコンパスを使って作図しなさい。作図に使った線は残しておきなさい。
【条件】
・点Pは、辺AB上にある。
・点Pと直線AC、直線BCとの距離は等しい。
【解答】
① 6
② -11
③ 5a+3b
④ 7ab²
⑤ 4+2√3
⑥ a(x+4)(x-4)
⑦ 20/3π(cm²)
⑧ イ、ウ
⑨ ア、エ
⑩ 下記図
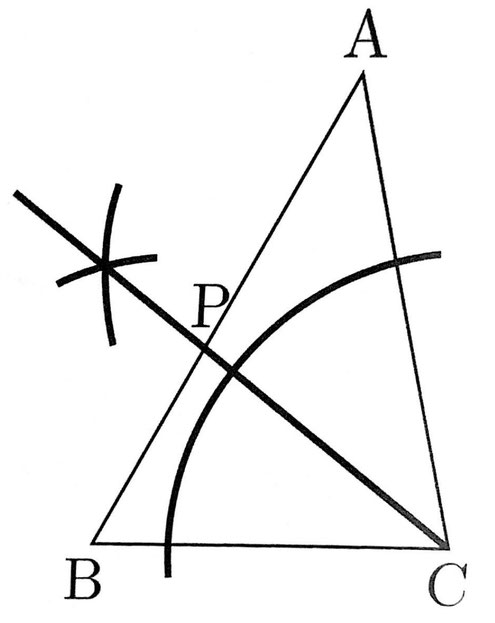
【解説】
⑧ 通る点をそれぞれxとyに代入すればよい。
⑩ ∠ACBの二等分線と辺ABの交点が点Pとなる。
太郎さんたちは、生徒会で資源ごみを回収し、近所のリサイクル業者に持ち込む取り組みをしています。そこでは、チラシに示すような比率でポイントが与えられます。①、②に答えなさい。

① チラシに示された内容に従って、次の数量の関係を不等式で表しなさい。
ペットボトルakgと新聞紙bkgのポイントの合計は、500ポイント以上である。
② 太郎さんたちは、アルミ缶とスチール缶を合わせて39kg持ち込んだところ、1160ポイントが与えられました。(1)、(2)に答えなさい。
(1)持ち込んだアルミ缶をxkg、スチール缶をykgとして連立方程式をつくりなさい。
(2)持ち込んだアルミ缶とスチール缶は、それぞれ何kgであるかを求めなさい。
【解答】
① 20a+7b≧500
② (1) x+y=39,45x+10y=1160
② (2) アルミ缶22kg、スチール缶17kg
【解説】
題意にそって式を立て、計算を行っていけばよい。
図1のように、関数y=ax²のグラフ上に点Aが、関数y=-x²のグラフ上に点Bがあります。2点A,Bのx座標は等しく、ともに正であるとします。①、②に答えなさい。ただし、a>0、点Oは原点とします。
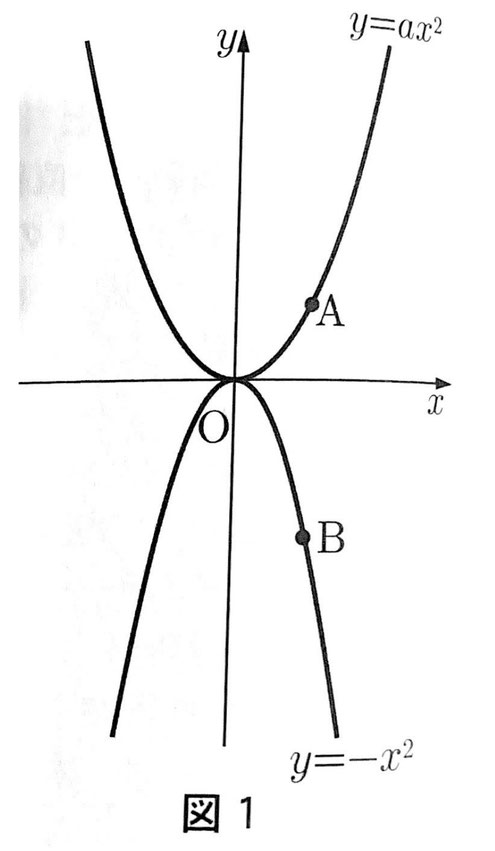
① 点Aの座標が(2,2)のとき、(1)~(3)に答えなさい。
(1)aの値を求めなさい。
(2)点Bのy座標を求めなさい。
(3)関数y=-x²のグラフ上に点Pがあり、△OABと△PABの面積の比が2:3となるとき、点Pのx座標をすべて求めなさい。
② a=1/3とします。図2のように、関数y=1/3x²のグラフ上に、点Aとy座標が等しくx座標が異なる点Cを取ります。また、関数y=-x²のグラフ上に、点Bとy座標が等しくx座標が異なる点Dを取り、四角形ACDBを作ります。(1)(2)に答えなさい。
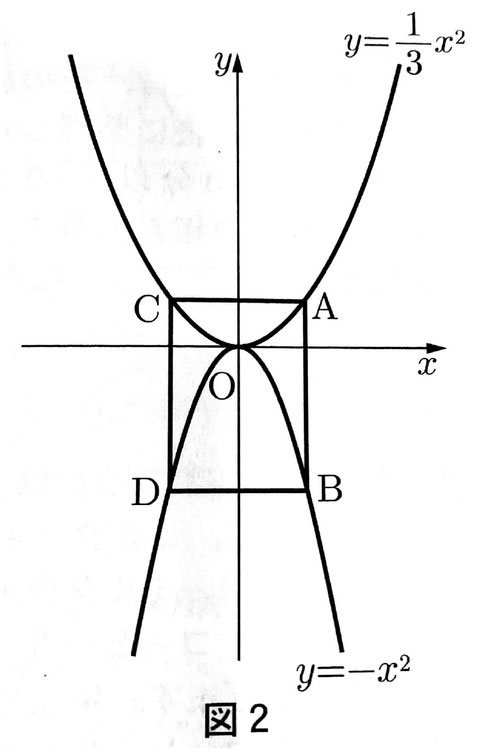
(1)点Aのx座標をtとするとき、線分ACの長さをtを使って表しなさい。
(2)四角形ACDBの周の長さが12となるとき、点Aの座標を求めなさい。
【解答】
① (1)a=1/2 (2)-4 (3)-1.5
② (1)2t (2)A(3/2,3/4)
【解説】
① (3)原点Oと直線ABとの距離は2であるから、点Pと直線ABとの距離が3になればよい。
② (2)AB=t²+1/3t²=4/3t²なので、条件より、(2t+4/3t²)×2=12 2t²+3t-9=0 t=-3,3/2 t>0より t=3/2
花子さんと次郎さんのクラスでは、文化祭でさいころを使ったゲームを企画しています。<企画ノートの一部>と<会話>を読んで、①~④に答えなさい。ただし、さいころの1から6までの目の出方は、同様に確からしいものとします。
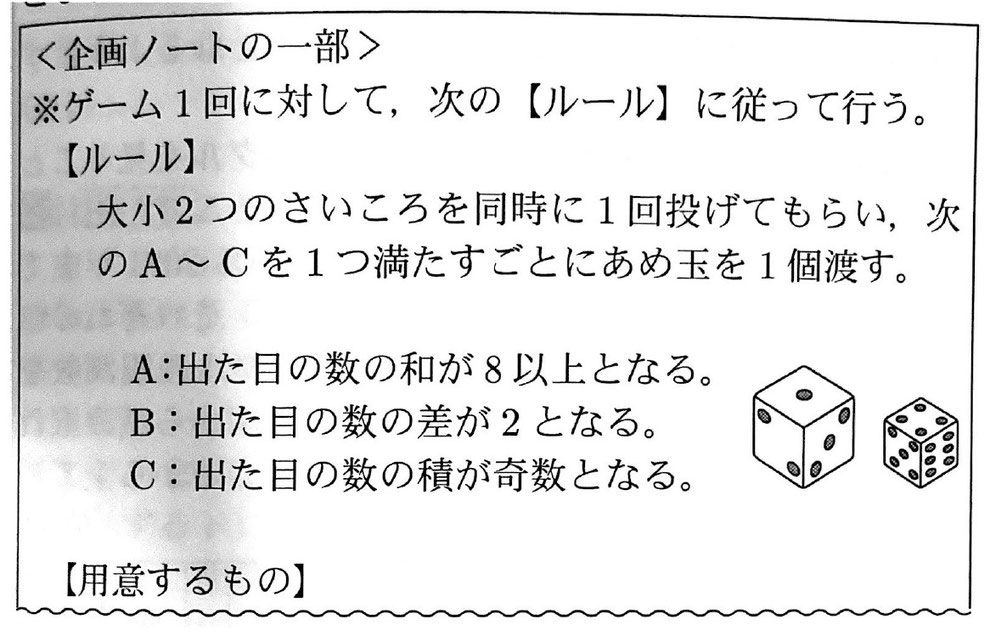
<会話>
花子:ゲームを1回行う時、渡す飴玉は0個の時もあれば3個のときもあるね。例えば、ゲームを1回行う時、大きいさいころで6の目、小さいさいころで4の目が出たら、渡す飴玉は(1)個だね。
次郎:A~Cのうちでは、どれが起こりやすいのかな。
花子:(あ)それぞれの起こる確率を比較すれば、起こりやすさを判断することができるよ。
次郎:なるほど、そうだね。
花子:それから、文化祭では飴玉を用意しないといけないけれど、どのくらいあればいいかな。
次郎:文化祭の時間内で出来るゲームの回数を最大1800回として計算してみよう。例えば、Bの起こる確率は(2)だから、1800回のうちBの起こる回数の割合が(2)であると考えられるので、(い)Bがおよそ何回起こるかを推定することができるよ。
花子:そうすると、渡す飴玉の数がどれくらいになるか分かるね。
次郎:(う)AとCについてもBと同じように考えれば、文化祭で渡す飴玉の総数がどのくらいになるか計算することができるよ。
花子:およその数が分かると、文化祭の準備はスムーズにできるね。
① (1)、(2)に適当な数を書きなさい。
② 下線部(あ)について、AとCでは、どちらの方が起こりやすいといえますか。それぞれの確率を使って説明しなさい。
③ 下線部(い)について、ゲームを1800回行うとき、Bがおよそ何回起こるかを求めなさい。ただし、式も書きなさい。
④ 下線部(う)について、花子さんと次郎さんは、文化祭でゲームを1800回行う時、渡す飴玉の総数がどのくらいになるか計算してみました。計算した結果、渡す飴玉の総数として最も適当なのは、ア~エのうちではどれですか。一つ答えなさい。
ア およそ800個
イ およそ1200個
ウ およそ1600個
エ およそ2000個
【解答】
① (1)2 (2)2/9
② (例)Aの起こる確率は15/36=5/12、Cの起こる確率は9/36=1/4となり、Aの起こる確率の方が大きいから、Aの方が起こりやすい。
③ (式)1800×2/9=400 およそ、400回
④ ウ
【解説】
④ Aが起こるのは、およそ1800×5/12=750回。Cが起こるのは、およそ1800×1/4=450回。よって、750+400+450=1600個
図1は、底面が正方形で側面が二等辺三角形の正四角錐OABCDです。①~④に答えなさい。
【正四角錐OABCDの説明】
・OA=6cm
・AB=4cm
・点Hは正方形ABCDの対角線の交点
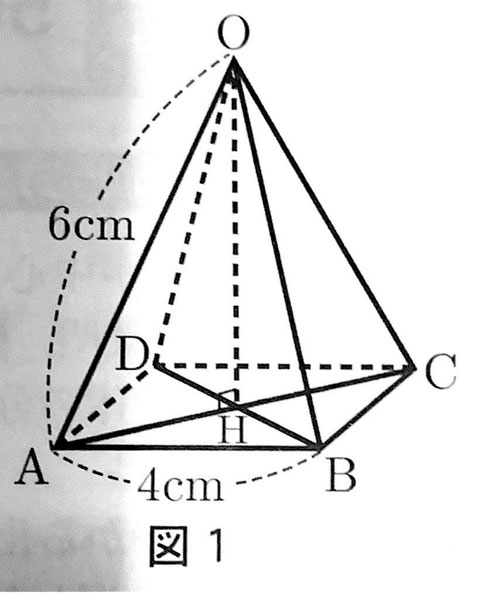
① 図1について正しく述べているのは、ア~エのうちではどれですか。一つ答えなさい。
ア 直線OAと直線BCは平行である。
イ 直線OBと直線ODはねじれの位置にある。
ウ 直線ADと平面OBCは平行である。
エ 平面OABと平面ABCDは垂直である。
② 線分AHの長さを求めなさい。
③ 正四角錐OABCDの体積を求めなさい。
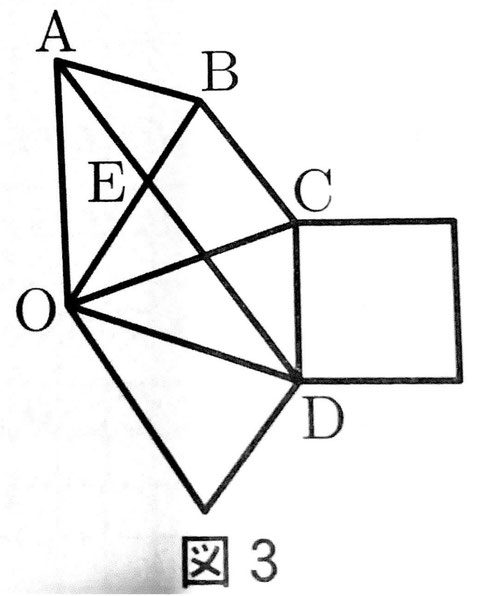
④ 図2のような、正四角錐OABCDの点Aから、辺OBと辺OCを通って点Dまで、ひもの長さが最も短くなるようにひもをかけます。また、図3は、正四角錐OABCDの展開図であり、点Eは、線分ADと線分OBとの交点です。(1)、(2)に答えなさい。
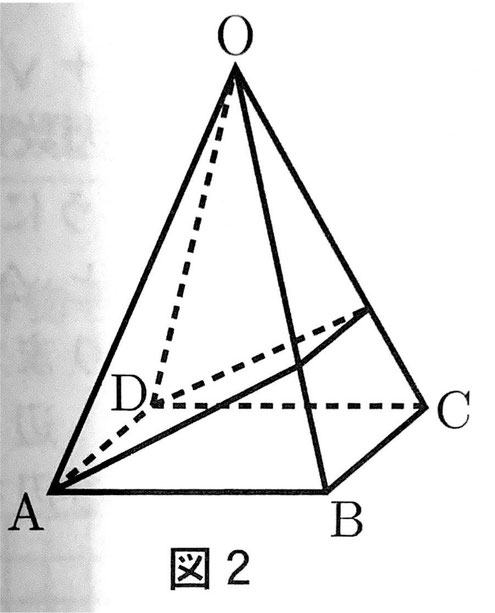
(1)図3において、△OAB∽△AEBであることは次のように証明することができます。(あ)~(う)に当てはまるものとして最も適当なのは、ア~カのうちではどれですか。それぞれ一つ答えなさい。また(え)には証明の続きを書き、証明を完成させなさい。
証明
△OABと△AEBにおいて、∠AOB=∠xとすると、
△OABはOA=OBの二等辺三角形だから、
∠OAB=(あ)である。
また、△OADは∠AOD=(い)、OA=ODの二等辺三角形だから、∠OAD=(う)である。
(え)
△OAB∽△AEBである。
ア 2∠x
イ 3∠x
ウ 90°-∠x
エ 90°-1/3∠x
オ 90°-1/2∠x
カ 90°-3/2∠x
(2)点Aから点Dまでかけたひもの長さを求めなさい。
【解答】
① ウ
② 2√2cm
③ 32√7/3cm³
④ (1) (あ)オ (い)イ (う)カ
④ (1) (え)∠EAB=∠OAB-∠OAD=(90°-1/2∠x)-(90°-3/2∠x)=∠x
よって、∠AOB=∠EAB…(ⅰ)
また、共通な角だから、∠OBA=∠ABE…(ⅱ)
(ⅰ)(ⅱ)から2組の角がそれぞれ等しいので、
(△OAB∽△AEBである)
④ (2) 92/9cm
【解説】
③ OH=2√7cm
④ (2)OA:AB=6:4=3:2
BE=4×2/3=8/3(cm) OE=6-8/3=10/3(cm)
ADとOCの交点をFとすると、
EF=10/3×2/3=20/9(cm)
AD=AE+EF+FD=4+20/9+4=92/9(cm)
家庭教師のやる気アシストでは、毎年スタッフが関西エリア各府県の入試問題を分析し、例年の傾向や次年度に向けての対策を行っています!
教育の現場は時代に合わせて目まぐるしく変化していくため、毎年対策を考えていく必要があります。「家庭教師って塾に比べて受験対策とかしっかりしてくれるの…?」とご質問いただくことも多いですが、ご安心ください!家庭教師だからこそ、お子さんの志望校、志望校の傾向など個々に合わせてより細やかなサポートをすることができるんです!
受験指導について気になることやわからないことがあればまずはアシストまでご連絡ください。専門スタッフがお子さんの受験勉強についてご相談に乗らせていただきます!
お子さんにとって「成果が出る勉強法」ってどんな勉強法だと思いますか?
お子さんそれぞれに、個性や性格、学力の差もあります。そんな十人十色のお子さん全員に合う勉強法ってなかなかないんです。
たからこそ、受験生の今だけでもお子さんだけの勉強法で受験を乗り越えてみませんか?
やる気アシストには、決まったカリキュラムはありません。お子さんの希望や学力、得意や不得意に合わせて、お子さんだけのカリキュラムで指導を行っていきます。また、勉強法もお子さんそれぞれに合う合わないがあります。無料体験授業では、お子さんの性格や生活スタイルを見せていただき、お子さんにとって効率的な成果の出る勉強のやり方をご提案させて頂きます。

