







大阪府の2021年3月実施の令和3年度(2021年度)入学者の公立高校入試問題の解説をしています。
受験勉強において、過去問を解くことはとても効果的な勉強法です。ぜひ、受験までに一度挑戦し、問題の傾向を掴んでおきましょう。合わせて、対策などをたてられるととても良いですね。
また、過去問で苦手な点が見つかった場合は、そこを中心に試験日当日までにしっかりと対策しておきましょう。
大阪府の数学問題は、レベル別にABCの問題が用意されています。受験する学校によりどの問題を採用するかが異なります。
難易度は、Aが易、Bがやや難、Cが難となっています。レベル差が顕著なので、各問題に対応する対策をとる必要があります。
【大阪府】令和3年度一般入学者選抜の過去問はこちらから
数学Aの過去問題はこちら>>
数学Bの過去問題はこちら>>
数学Cの過去問題はこちら>>
問1:正負の数の計算をする問題です。
10 - 2 × 8
【・答え ー6】
10-2×8=10ー16=ー6
問2:正負の数の計算をする問題です。
-12 ÷(- 6/7 )
【・答え 14】
÷○ → ×1/○ に変換する。
ー12÷(ー7/6)=ー12×(ー6/7)=14
問3:正負の数の計算をする問題です。
5²+ (-21 )
【・答え 4】
5²+(ー21)=25-21=4
問4:文字と式の計算をする問題です。
6x - 3 - 4 ( x + 1 )
【・答え 2x-7】
一旦バラした後、同じ文字・次数同士で計算する。
6xー3ー4(x+1)=6xー3ー4x-4=2x-7
問5:文字と式の計算をする問題です。
5x × (-x2 )
【・答え ー5x³】
同じ文字同士のかけ算は次数を付けることで表す。
5x×(ーx²)=ー5x³
問6:平方根を含む式を計算する問題です。
√7 + √28
【・答え 3√7】
平方根の中身を素因数分解して、根の値を合わせると計算できる。
√7+√28=√7+2√7=3√7
問1:a=ー3のときのーa+8を求める問題です。
a =-3 のとき,-a + 8 の値を求めなさい。
【・答え 11】
aにー3を代入する。
ー(ー3)+8=11
問2:かかった時間についての正しい式を選ぶ問題です。
次のア~エの式のうち,「a m の道のりを毎分 70 m の速さで歩くときにかかる時間(分)」を
正しく表しているものはどれですか。一つ選び,記号を○で囲みなさい。
ア a + 70 イ 70a ウ a/70 エ 70/a
【・答え ウ】
amの道のりを毎分70mの速さで歩くときにかかる時間を求めるので、
時間=道のり÷速さより、
a/70となり、ウと同じ答えになる。
問3:無理数であるものを選ぶ問題です。
次のア~エの数のうち,無理数であるものはどれですか。一つ選び,記号を○で囲みなさい。
ア 1/3 イ√ 2 ウ 0.2 エ √9
【・答え イ】
アの1/3、ウの0.2→1/5、エの√9→3 これらの値は、整数/整数であらわされているので有理数。
ィの√2は整数/整数で表すことが出来ないので無理数となる。
問4:比例式を使って、xを求める問題です。
比例式 x:12 = 3:2 を満たす x の値を求めなさい。
【・答え 18】
x:12=3:2
→ x×2=12×3
→ 2x=36
→ x=18
問5:連立方程式 5x+2y=ー5 3x-2y=13 についてxとyを解く問題です。
連立方程式
⎧ 5x+2y =-5
⎩ 3x-2y = 13 を解きなさい。
【・答え x=1,y=ー5】
5x+2y=ー5を①、3x-2y=13を②とする。
①+②をすると、
5x+2y+3x-2y=ー5+13
→8x=8
→x=1
これを①に代入すると、
5×1+2y=ー5
→2y=ー10
y=ー5
問6:二次方程式を解く問題です。
二次方程式 x² - 4x - 21 = 0 を解きなさい。
【・答え x=3,x=ー7】
因数分解する。どのように分ければいいか分からない人は、ー21をいくつかのかけ算で表現する方法を考えるとよい。
それでも分からない人は解の公式を解ける。
x²ー4x-21=0
(x+3)(x-7)=0
x=ー3,x=7
⑺ 右の表は,水泳部員 20 人の反復横とびの記録を度数分布表にまとめたものである。記録が 55 回以上の部員の人数が,水泳部員20 人の 30 %であるとき,表中の x,y の値をそれぞれ求めなさい。
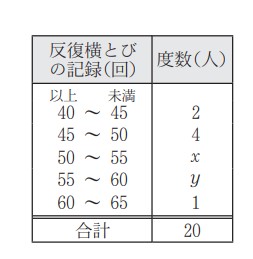
問7:資料の度数を求める問題です。
【・答え x=8,y=5】
資料と問題文から方程式を立てて、xとyの値を求めます。
資料からは、度数が20人となっているので、xとyの合計は20-(2+4+1)=13より、
x+y=13 ①
問題文から「記録が55回以上の部員の人数が、水泳部員20人の30%」とあるので、
55回以上の部員がy+1(人)
20人の30%は、20×30/100=6より、
y+1=6
→y=5
これを①に代入すると、
x+5=13
→x=8
⑻ 二つの箱 A,B がある。箱 A には自然数の書いてある 5 枚のカード 1 , 2 , 3 , 4 , 5 が入っており,箱 B には奇数の書いてある 3 枚のカード 1 ,3 ,5 が入っている。A,B それぞれの箱から同時にカードを 1 枚ずつ取り出すとき,取り出した 2 枚のカードに書いてある数の和が4 の倍数である確率はいくらですか。A,B それぞれの箱において,どのカードが取り出されることも同様に確からしいものとして答えなさい。
問8:ひいた2枚のカードの和が4の倍数になる確率を求める問題です。
【・答え 4/15】
2枚のカードの和が4の倍数になる組み合わせは、
(A,B)=(1,3)(3,1)(3,5)(5,3)
4通りである。
一方、全てのカードの組み合わせ方法は、Aが5枚、Bが3枚あるので、
5×3=15
の15通りであるから、その確率は、
4/15
⑼ 図において,m は関数 y =ax2
( a は定数)のグラフを
表す。A は m 上の点であり,その座標は(-4 ,3 )である。
a の値を求めなさい。
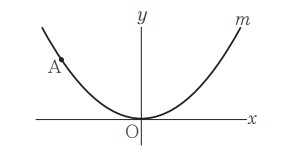
問9:二次関数について傾きを求める問題です。
【・答え 3/16】
y=ax²にAの座標(ー4、3)を代入すると、
3=a×(ー4)²
→3=16a
→a=3/16
⑽ 図において,△ABC は正三角形である。△DBE は,△ABC を,点 B を回転の中心として,時計の針の回転と反対の向きに 100°回転移動したものである。180°より小さい角∠ABE の大きさを求めなさい。
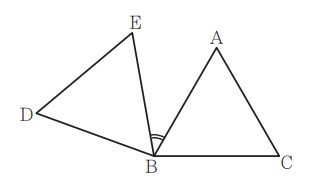
問10:回転移動させた図形と、元の図形の間の角度を求める問題です。
【・答え 40度】
三角形DBEは点Bを軸に反時計周りに回転させるので、
∠EBC=100度である。
また、三角形ABCは正三角形なので、
∠ABC=60度である。
以上の事から、∠EBDは
∠EBD=∠EBCー∠ABC
=100-60=40
∠EBD=40度
⑾ 右図において,四角形 ABCD は長方形であり,AB = 6 cm,AD = 3 cm である。四角形 ABCD を直線 DC を軸として 1 回転させてできる立体をPとする。
① 次のア~エのうち,立体Pの見取図として最も適しているものはどれですか。
一つ選び,記号を○で囲みなさい
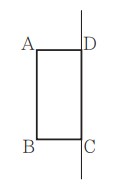
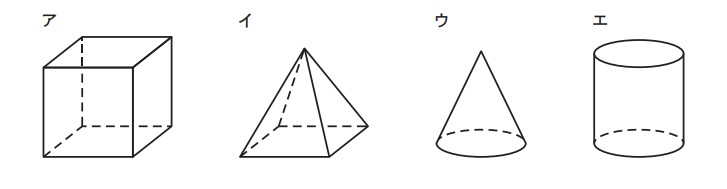
② 円周率をπとして,立体Pの体積を求めなさい。
問11:直方体の展開図について、見取り図・体積を求める問題です。
【・答え ①:エ ②:54π】
②:辺BCからなる面を底面として計算する。半径は3cmなので、面積は3×3×π=9πcm²
辺ABを高さとすると、円柱の体積は6×9π=54πcm³である。
学校の花壇に花を植えることになった E さんは,花壇の端のレンガから 10 cm離して最初の花を植え,あとは 25 cm間隔で一列に花を植えていくことにした。下図は,花壇に花を植えたときのようすを表す模式図である。
下図において,O,P は直線ℓ上の点である。「花の本数」がx のときの「線分 OP の長さ」を y cm とする。x の値が 1 増えるごとに y の値は 25 ずつ増えるものとし,x = 1 のとき y = 10であるとする。
次の問いに答えなさい
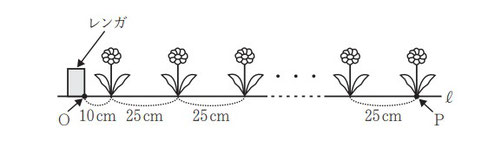

問1:xとyの関係を表した表の空欄を埋める問題です。
次の表は,x と y との関係を示した表の一部である。表中のア,イに当てはまる数をそれぞれ 書きなさい。
【・答え ア:85 イ:210】
x=4のときは、3コ分の隙間(3×25=75cm)と最初の間隔(10cm)があるので、線分APの長さは
75+10=85(cm)である。
x=9のときは、8コ分の隙間(8×25=200cm)と最初の間隔(10cm)があるので、線分APの長さは
200+10=210(cm)である。
問2:yをxの式で表す問題です。
x を自然数として,y を x の式で表しなさい。
【・答え 25xー15】
問1より、線分APの長さは本数に応じて増えていく長さと、本数によらず変わらない(最初の間隔)長さの足し合わせであるとわかる。したがって、
(線分APの長さ)=(花同士の間隔)×(花の本数ー1)+(最初の間隔)
と表せる。これを文字式に置き換えると
y=25(xー1)+10
→y=25x-15
となる。
問3:y=560となるときのxの値を求める問題です。
y = 560 となるときの x の値を求めなさい。
【・答え 23】
問2で求めた式にy=560を代入すれば求められる。
y=25xー15 → 560=25xー15
25x=575
x=23
図において,△ABC は∠ABC = 90°の直角三角形であり,AB = 7 cm,BC = 5 cm である。
四角形 DBCE は平行四辺形であり,D は辺 AC 上にあ っ て A,C と 異 な る。F は,C か ら 辺 DE にひいた垂線と辺 DE との交点である。
次の問いに答えなさい。
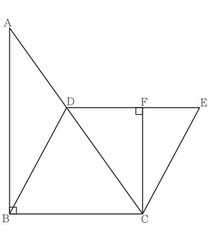
問1:四角形DBCEの内角∠DBCをa°としたときの四角形DBCEの内角∠BCEの大きさをaを使って表す問題です。
四角形 DBCE の内角∠DBC の大きさを a°とするとき,四角形 DBCE の内角∠BCE の大きさを a を用いて表しなさい。
【・答え (180-a)度】
四角形DBCEは平行四辺形なので、
∠DBC+∠BCE=180°とあらわすことができるので、
∠BCE=180°ー∠DBC
→ ∠BCE=180°ーa°
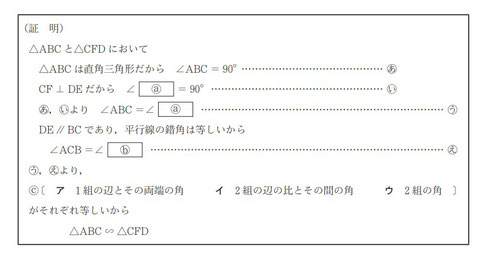
問2:問題中に示された「△ABC∽△CFD」の証明の空欄ⓐⓑに適している「角を表す文字」をそれぞれ答える問題です。また、空欄Ⓒに適した選択肢を選ぶ問題です。
次は,△ABC ∽ △CFD であることの証明である。 ⓐ , ⓑ に入れるのに適している「角を表す文字」をそれぞれ書きなさい。また,ⓒ 〔 〕から適しているものを一つ選び,記号を○で囲みなさい。
【・答え ⓐ:CFD ⓑ:CDF Ⓒ:ウ】
ⓐ:△CFDの内、∠CFDが90度となる。
ⓑ:平行線の錯角は等しいことを利用して、∠ACB=∠CDFを導く。
Ⓒ:”う”と”え”の条件で対応する角が等しくなることを示している。
問3:三角形FCEの面積を求める問題です。
FC = 4 cm であるときの△FCE の面積を求めなさい。途中の式を含めた求め方も書くこと。
【・答え 30/7】
まず、FDの長さを求める
問2より、△ABC∽△CFDなので、対応する辺の長さは比例している
AB:BC=CF:FD
→7:5=4:FD →7FD=5×4
→FD=20/7 ①
次に、辺FEの長さを求める
四角形CBDEは平行四辺形なので、BC=DEと①より、
BC=DE → BC=DF+FE → 5=20/7+FE
→FE=5-20/7=15/7 ②
最後に三角形FCEの面積を求める
∠CFE=90度、FC=4、②から三角形FCEの面積は
15/7×4×1/2=30/7
問1:2×(ー3)²ー22を計算する問題です。
2 × (-3 )2 - 22 を計算しなさい。
【・答え ー4】
累乗を計算 → 乗除を計算 →加減を計算する。
2×(ー3)²ー22
=2×9ー22
=18ー22
=ー4
問2:4(xーy)+5(2x+y)を計算する問題です。
4 ( x - y )+ 5 ( 2x + y ) を計算しなさい。
【・答え 14x+y】
()を外してから計算する
4(xーy)+5(2x+y)
=4x-4y+10x+5y
=14x+y
問3:18b×(ーa²)÷3abを計算する問題です。
18b × (-a2 )÷ 3ab を計算しなさい。
【・答え ー6a】
数字と文字をそれぞれ計算する。(÷〇 → ×1/〇に変換してもよい)
18b×(ーa²)÷3ab
=18b×(ーa²)×1/3ab
=-6a
問4:x(x+7)ー(x+4)(xー4)を計算する問題です。
x( x + 7 )- ( x + 4 ) ( x - 4 ) を計算しなさい。
【・答え 7x+16】
一旦展開 → 文字と数をそれぞれまとめる。
x(x+7)ー(x+4)(xー4)
=x²+7xーx²+16
=7x+16
問5:(2-√5)² を計算する問題です。
(2-√5)²を計算しなさい。
【・答え 9ー4√5】
(2-√5)²
=4ー4√5+5
=9ー4√5
問6:正七角形の内角の和を求める問題です。
正七角形の内角の和を求めなさい。
【・答え 900度】
180×(7-2)=900
正七角形を7つの二等辺三角形に分けて考える。
それぞれの三角形の頂点の角度は
360÷7=360/7度
その他の2つの角は等しいので、
(180-360/7)度
これが7個あるので、内角の和は
(180-360/7)×7=900度
問7:選択肢の中から一番値が大きいものを答える問題です。
a を正の数とし,b を負の数とする。次のア~エの式のうち,その値が最も大きいものはどれですか。一つ選び,記号を○で囲みなさい。
ア a
イ b
ウ a + b
エ a - b
【・答え エ】
bは負の数なので、-bは負の数となる。
a-bは正の数+正の数となるので、一番値が大きくなる。
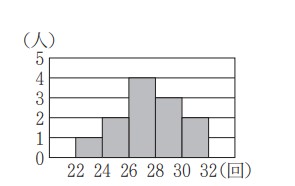
問8:ヒストグラムの中で一番多い階級の相対度数を求める問題です。
図は,柔道部員 12 人の上体起こしの記録をヒストグラムに表したものである。度数が最も多い階級の相対度数を小数で答えなさい。ただし,答えは小数第 3 位を四捨五入して小数第 2 位まで書くこと。
【・答え 0.33】
一番多い階級は26~28回の4人。
部員は全員で12人いるので、相対度数は
4÷12=0.333より0.33
問9:5枚のカードから2枚引き、出た2枚の数を掛けて2で割ったものが奇数である確率を求める問題です。
3 から 7 までの自然数が書いてある 5 枚のカード 3 , 4 , 5 , 6 , 7 が箱に入っている。
この箱から 2 枚のカードを同時に取り出し,取り出した 2 枚のカードに書いてある数の積を a とするとき, a/2 の値が奇数である確率はいくらですか。どのカードが取り出されることも同様に確からしいものとして答えなさい
【・答え 3/10】
取り出し方は
(3,4)、(3,5)、(3,6)、(3,7)、(4,5)、(4,6)、(4,7)、(5,6)、(5,7)、(6,7)の10通り
この中で積を2で割った時奇数となるのは(3,6)、(5,6)、(6,7)の3通り。
よって、求める確率は3/10
図において, 四角形ABCDはAD // BCの台形であり, ∠ADC=∠DCB= 90°,AD = 2 cm,BC = DC = 3 cm である。四角形 ABCD を直線 DC を軸として1 回転させてできる立体の体積は何 cm3 ですか。円周率をπとして答えなさい。
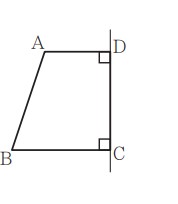
問10:図を回転させてできた立体の体積を求める問題です。
【・答え 19π】
図を三角形にしてから円錐の体積を出し、余分な円錐の体積を引くという方法で求める。
辺BAを点Aの方向に伸ばし、辺CDと交わる点を点Eとする。
三角形BCEからなる円錐の体積を求める。
線分DE(=xcm)は、三角形EADと三角形EBCが相似であるため、
ED:EC=AD:BC
→ x:x+3=2:3
→ x×3=2×(x+3)
x=6となる
体積は、
(6+3)×(3²×π)×1/3=27π
ここから、
三角形EADからなる円錐の体積を引けばいいので、
27πー6×(2²×π)×1/3
=19π
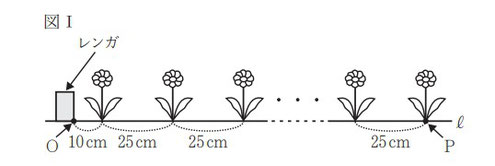
学校の花壇に花を植えることになった E さんは,花壇の端のレンガから 10 cm 離して最初の花を植え,あとは等間隔で一列に花を植えていくことにした。E さんは,図Ⅰのような模式図をかいて 25 cm 間隔で花を植える計画を立てた。
図Ⅰにおいて,O,P は直線ℓ上の点である。「花の本数」が1 増えるごとに「線分 OP の長さ」は 25 cm ずつ長くなるものとし,「花の本数」が 1 のとき「線分 OP の長さ」は 10 cm であるとする。
次の問いに答えなさい。

図Ⅰにおいて,「花の本数」が x のときの「線分 OP の長さ」を y cm とする。\
①:xとyの関係を表した表の空欄を埋める問題です。
【・答え ア:85 イ:210】
x=4のときは、3コ分の隙間(3×25=75cm)と最初の間隔(10cm)があるので、線分APの長さは
75+10=85(cm)である。
x=9のときは、8コ分の隙間(8×25=200cm)と最初の間隔(10cm)があるので、線分APの長さは
200+10=210(cm)である。
②:yをxの式で表す問題です。
【・答え 25xー15】
問1より、線分APの長さは本数に応じて増えていく長さと、本数によらず変わらない(最初の間隔)長さの足し合わせであるとわかる。したがって、
(線分APの長さ)=(花同士の間隔)×(花の本数ー1)+(最初の間隔) 式1
と表せる。これを文字式に置き換えると
y=25(xー1)+10
→y=25x-15
となる。
③:y=560となるときのxの値を求める問題です。
【・答え 23】
問2で求めた式にy=560を代入すれば求められる。
y=25xー15 → 560=25xー15
25x=575
x=23
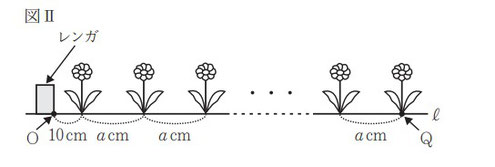
問2:問1と同じ線分の長さで、本数を31本に増やした時の間隔の長さを求める問題です。
E さんは,図Ⅰのように 25 cm 間隔で 28 本の花を植える計画を立てていたが,植える花の本数が 31 本に変更になった。そこで E さんは,花壇の端のレンガから最後に植える花までの距離を変え ないようにするために,図Ⅱのような模式図をかいて花を植える間隔を考え直すことにした。
図Ⅱにおいて,O,Q は直線ℓ上の点である。「花の本数」が 1 増えるごとに「線分 OQ の長さ」 は a cm ずつ長くなるものとし,「花の本数」が 1 のとき「線分 OQ の長さ」は 10 cm であるとする。
図Ⅰにおける「花の本数」が 28 であるときの「線分 OP の長さ」と,図Ⅱにおける「花の本数」 が 31 であるときの「線分 OQ の長さ」とが同じであるとき,a の値を求めなさい。
【・答え a=45/2】
線分OPの長さを求める
問1の②で求めたy=25x-15にx=28を代入すると
y=25×28-15=685
線分OQの長さを求める
問1の②式1を参考にして
10+a×(31-1)=10+30a
OP=OQとなるので
685=10+30a
→ a=45/2
図Ⅰ,図Ⅱにおいて,m は関数 y = 1/8 x² のグラフを表す。
次の問いに答えなさい
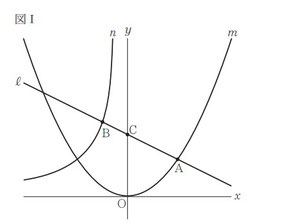
図 Ⅰ に お い て,n は 関 数 y =- 27/x ( x < 0 )の グ ラ フ を 表 す。A は m 上 の 点 で あ り, そ のx 座標は 6 である。B は n 上の点であり,そのx 座標は - 3 である。ℓは,2 点 A,B を通る直線である。C は,ℓと y 軸との交点である。
①:yの変域を求める問題です。
次の文中の ㋐ , ㋑ に入れるのに
適している数をそれぞれ書きなさい。
関数 y = 1/8 x²について,
x の 変 域 が -7 ≦ x ≦ 5 の と き のy の変域は ㋐ ≦ y ≦ ㋑である。
【・答え ㋐:0、㋑:49/8】
㋐ x=0の時yは最小値を取るので、y=1/8×0²=0
㋑ x=ー7の時yは最大値を取るので、y=1/8×(ー7)²=49/8
②:Bのyの座標を求める問題です。
B の y 座標を求めなさい。
【・答え 9】
y=ー27/xにx=ー3を代入して、
y=(ー27)/(ー3)=9
③:Cのyの座標を求める問題です。
C の y 座標を求めなさい。
【・答え 9】
点Aと点Bの座標から直線lの式を求めてから、点Cの座標を求める。
点Aのy座標はx=6を代入して、y=1/8×6²=9/2
点A(6,9/2)、点B(ー3,9)より直線ⅼの傾きは
(9/2ー9)/(6-(ー3))=ー1/2
より、直線ⅼの式は
点cのy座標をⅽとすると
y=ー1/2ⅹ+ⅽ
点Bを通るので、点Bの座標を代入して、
9=ー1/2×(ー3)+ⅽ
→ ⅽ=15/2
問2:Eのⅹ座標を求める問題です。
図Ⅱにおいて,D,E は m 上の点である。D のx 座標は 4 であり,E の x 座標は D の x 座標より大 き い。E の x 座 標 を t と し,t > 4 と す る。F は,D を通り y 軸に平行な直線と,E を通り x 軸に平行な直線との交点である。線分 FD の長さが線分 FE の長さより 8 cm 長いときの t の値を求めなさい。途中の式を含めた求め方も書くこと。
ただし,原点 O から点( 1 ,0 )まで,原点 O から点( 0 ,1 )までの距離はそれぞれ 1 cm であるとする。
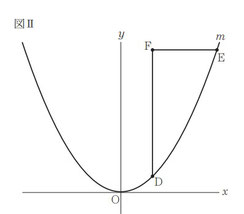
【・答え tの値 12】
点Ⅾ、E、Fの座標を求めてから、線分ⅮF、EFの長さを比較する
求め方
y=1/8×ⅹ²にx=4を代入すると、y=2より点D(4,2)
x=tを代入すると、y=1/8×t²より、点E(t,1/8×t²)
点D、Eから点F(4,1/8×t²)
よって、
ⅮF=1/8×t²ー2、EF=tー4
ⅮF=EF+8
→1/8×t²ー2=tー4+8
→t²ー8tー48=0
→(t+4)(tー12)=0、t>4より
t=12
[Ⅰ] 図Ⅰにおいて,四角形 ABCD は内角∠ABC が鋭角の平行四辺形である。△EDC は ED = EC の二等辺三角形であり,E は直線 BC 上にある。F は,A から辺 BC にひいた垂線と辺 BC との交点である。G は,C から辺 ED にひいた垂線と辺 ED との交点である。
次の問いに答えなさい。
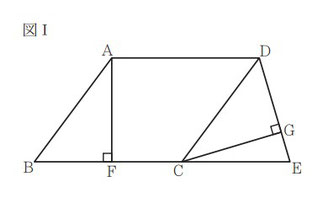
問1:△ABF≡△CDGであることを証明する問題です。
△ABF ≡ △CDG であることを証明しなさい。
△ABF、△CDGにおいて、
四角形ABCDが平行四辺形よりAB=CD ㋐
∠AFB=∠CGD=90° ㋑
AB//DCより
∠ABF=∠DCE
△EDCはED=ECの二等辺三角形なので
∠CDG=∠DCE(=∠ABF) ㋒
㋐、㋑、㋒より
1つの辺とその両端の∠が等しいので
△ABF≡△CDG
問2:△CEGの面積をa,bを使って表す問題です。
四角形 ABCD の面積を a cm2, 四角形 AFED の面積を b cm2 とするとき,△CEG の面積を a,bを用いて表しなさい。
【・答え b-a】
四角形ABCD=a、四角形AFED=b
四角形AFED=四角形AFCD+三角形CDG+三角形CFG
四角形AFCD=四角形AFCD+三角形ABF
問1より△ABF≡△CDGなので、
四角形AFEDー四角形AFCD=三角形CFGとなるので、
b-a
[Ⅱ] 図Ⅱ,図Ⅲにおいて,立体 ABC-DEF は三角柱である。△ABC は∠ABC = 90°の直角三角形であり,AB = 4 cm,CB = 6 cm である。△DEF ≡ △ABC である。四角形 EFCB は 1 辺の長さが6 cm の 正 方 形 で あ り, 四 角 形 DFCA,DEBA は 長 方 形 で あ る。G は 辺 DF 上 の 点 で あ り,DG:GF = 4:3 である。
次の問いに答えなさい。
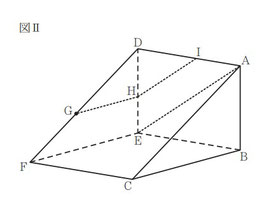
図Ⅱにおいて,A と E とを結ぶ。H は,G を通り辺 FE に平行な直線と辺 DE との交点である。I は,H を通り線分 AE に平行な直線と辺 AD との交点である。
①:ねじれの位置にある辺を選択肢の中から選ぶ問題です。
次のア~オのうち,辺 AB とねじれの位置にある辺はどれですか。すべて選び,記号を○で囲みなさい。
ア 辺 AD
イ 辺 CF
ウ 辺 DE
エ 辺 DF
オ 辺 FE
【・答え イ、エ、オ】
辺ABと交わらない、平行ではない辺を選ぶ。
②:線分DIの長さを求める問題です。
② 線分 DI の長さを求めなさい。
【・答え 24/7】
IH//AE、HG//EFより、
DI:IA=DH:HE=DG:GF=4:3
点Iは線分DIを4:3に分けているので、
DI=DA×4/(4+3)=6×4/7=24/7
図Ⅲにおいて,G と A,G と C とをそれぞれ結ぶ。J は辺 CB 上の点であり,3 点 A,J,Bを 結 ん で で き る △AJB の 内 角 ∠AJB の大きさは,△ABC の内角∠BAC の大きさと等しい。J と G とを結ぶ。立体 AGCJ の体積を求めなさい。
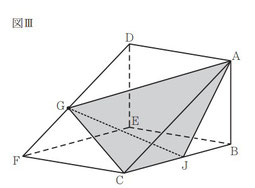
問4:立体AGCJの体積を求める問題です。
【・答え 40/3】
△AJCを底面として、体積を求める。
△ABC、△JBAにおいて
∠ABC=∠JBA(=90°)、∠CAB=∠AJBより、
2つの角が等しいので、△ABC∽△JBA
JBをxとおく
AB:JB=CB:AB
→4:x=6:4
→x=8/3
よって、CJ=6-8/3=10/3
△AJC=10/3×4×1/2=20/3
底面が△AJCの時、高さはAD=6となるので
20/3×6×1/3=40/3
問1:7a+b/3ー3a-5b/2を計算する問題です。
7a+b/3ー3a-5b/2を計算しなさい。
【・答え (5a+17b)/6】
分母を6に揃えて計算する。
7a+b/3ー3a-5b/2
=(7a+b)×2/6ー(3a-5b)×3/6
={(14a+2b)-(9a-15b}/6
=(5a+17b)/6
問2:(3/4×ab)²÷9a²b/8×(-2b)を計算する問題です。
(3/4×ab)²÷9a²b/8×(-2b)を計算しなさい。
【・答え ーb²】
÷〇 → ×1/〇にする。
(3/4×ab)²÷9a²b/8×(-2b)
=(3/4×ab)²×8/9a²b×(-2b)
=9a²b²/16×8/9a²b×(-2b)
=ーb²
問3:√3(√15+√3)ー10/√5を計算する問題です。
√3(√15+√3)ー10/√5を計算しなさい。
【・答え √5+3】
有利化・展開によって簡単な形にする → まとめる
√3(√15+√3)を展開すると3√5+3
10/√5を有利化すると
10×√5/√5×√5=10×√5/5=2√5
より、
√3(√15+√3)ー10/√5
=3√5+3ー2√5
=√5+3
問4:2(a+b)²-8=0を因数分解する問題です。
2(a+b)²-8=0を因数分解しなさい。
【・答え 2((a+b)-2)((a+b)+2)】
全体を2でくく
2(a+b)²-8=0
→ 2{(a+b)²-4}=0
→ 2{(a+b)²-2²}=0
→ 2{((a+b)-2)((a+b)+2)}=0
→ 2((a+b)-2)((a+b)+2)=0
問5:絶対値が自然数nよりも小さい整数の個数を求める問題です。
n を自然数とする。次の条件を満たす整数の個数を n を用いて表しなさい。
「絶対値が n より小さい。」
【・答え 2n-1】
-(n-1)から(n-1)までの個数なので、
(n-1)ー(-(n-1))=2n-1
問6:一つの内角の大きさが140°であるとき正多角形の内角の和を求める問題です。
一つの内角の大きさが 140°である正多角形の内角の和を求めなさい。
【・答え 1260°】
1つの外角の大きさは180°ー140°=40°
360°÷40°=9となるので、これは正九角形だとわかる
内角の和は、
180×(9-2)=1260
問7:選択肢の中から常に負の数aよりも小さくなるものを選ぶ問題です。
a を負の数とするとき,次のア~オの式のうち,その値がつねに a の値以下になるものはどれですか。すべて選び,記号を○で囲みなさい。
ア a + 2
イ a - 2
ウ 2a
エ a/2
オ -a²
【・答え イ、ウ】
ア:aに正の数を足しているので値は大きくなる
イ:aに正の数を引いているので値は小さくなる
ウ:負の数aを2倍しているので、値は小さくなる
エ:負の数を2で割っているので、0に近くなる為値は大きくなる
オ:0<a<1のとき値は小さくなり、1<aのとき値は大きくなる
5 人の生徒が反復横とびを行い,その回数をそれぞれ記録した。次の表は,それぞれの生徒の回数と B さんの回数との差を,B さんの回数を基準として示したものであり,それぞれの生徒の回数がB さんの回数より多い場合は正の数,少ない場合は負の数で表している。この 5 人の反復横とびの回数の平均値は 47.6 回である。B さんの反復横とびの回数を求めなさい。
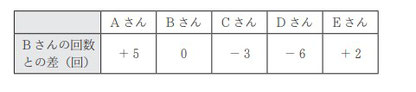
問8:Bさんの回数を周りとの差から求める問題です。
【・答え 48】
Bさんをx回とおいて、平均値を表すと
{(x+5)+x+(x-3)+(x-6)+(x+2)}/5
=(5x-2)/5
これが47.6回になるので、
(5x-2)/5=47.6
5x=47.6×5+2
x=48

問9:6枚のカードから2枚のカードを引き、条件にあう確率を求める問題です。
表が白色で裏が黒色の円盤が 6 枚ある。それらが図のように,左 端 か ら 4 枚 目 の 円 盤 は 黒 色 の 面 が 上 を 向 き, 他 の 5 枚 の円盤は白色の面が上を向いた状態で横一列に並んでいる。
1 から 6 までの自然数が書いてある 6 枚のカード 1 , 2 , 3 , 4 , 5 , 6 が入った箱から2 枚のカードを同時に取り出し,その 2 枚のカードに書いてある数のうち小さい方の数を a,大きい方の数を b とする。 図の状態で並んだ 6 枚の円盤について, 左端から a 枚目の円盤と左端から b 枚目の円盤の表裏をそれぞれひっくり返すとき,上を向いている面の色が同じである円盤が 3 枚以上連続して並ぶ確率はいくらですか。どのカードが取り出されることも同様に確からしいものとして答えなさい。
【・答え 8/15】
取り出した2枚カードの組み合わせは
(a,b)=(1,2)、(1,3)、(1,4)、(1,5)、(1,6)、(2,3)、(2,4)、(2,5)、(2,6)、(3,4)、(3,5)、(3,6)、(4,5)、(4,6)、(5,6)の15通り。
この中で同じ色の円盤が三枚以上連続して並んでいる組み合わせは、
(1,4)、(2,3)、(2,4)、(3,4)、(3,5)、(4,5)、(4,6)、(5,6)の8通り
確率は8/15
問9:√300ー3nの値が偶数となる値を全て求める問題です。
n を 2 けたの自然数とするとき, √300 - 3n の値が偶数となる n の値をすべて求めなさい。
【・答え n=52、88】
√300ー3n=√3(100-n) nは二けたの自然数
100-nが3×a²(aは正の偶数)であれば、√300ー3nの値が偶数となるので、
a=2のとき
100-n=3×2²=12 → n=88
a=4のとき
100-n=3×4²=48 → n=52
a=6のとき
100-n=3×6²=108 → n=ー8 となるので不適
n=52、88
問11:図を回転させてできた立体の表面積を求める問題です。
図において, 四角形ABCDはAD // BCの台形であり, ∠ADC=∠DCB=90°,AD = 2 cm,AB = 4 cm,BC = 3 cm である。四角形 ABCD を直線 DC を軸として 1 回転させてできる立体の表面積は何 cm2 ですか。円周率をπとして答えなさい。
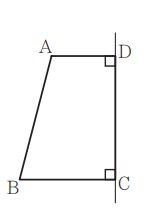
【・答え 33π】
図を三角形にしてから円錐の表面積を出し、余分な円錐の表面積を引くという方法で求める。
辺BAを点Aの方向に伸ばし、辺CDと交わる点を点Eとする。
三角形BCEからなる円錐の体積を求める。
線分AE(=xcm)は、三角形EADと三角形EBCが相似であるため、
EA:EB=AD:BC
→ x:x+4=2:3
→ x×3=2×(x+4)
x=8となる
表面積は、
(8+4)×3×π+3²×π+2²×π=47π
ここから、
三角形EADからなる円錐の側面の表面積を引いて、上面の表面積を足せばいいので、
47πー8×2×π+2²×π
=33π
図Ⅰ,図Ⅱにおいて,m は関数 y = 3/8 ×x² のグラフを表し,ℓは関数 y = 2x + 1 のグラフを表す。
次の問いに答えなさい。
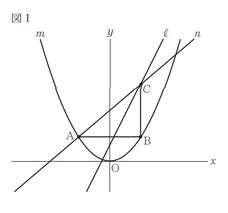
①:yの変域を求める問題です。
図Ⅰにおいて, A は m 上の点であり, その x 座標は-2 である。B は,A を通り x 軸に平行な直線とm との交点のうち A と異なる点である。C は,B を通り y 軸に平行な直線とℓとの交点である。
n は,2 点 A,C を通る直線である。
次の文中の ㋐ , ㋑ に入れるのに適している数をそれぞれ書きなさい。
関数 y = 3/8 ×x² について,
x の 変 域 が -3 ≦ x ≦ 1 の と き の
y の変域は ㋐ ≦ y ≦ ㋑
である。
【・答え ㋐:0、㋑:27/8】
㋐ x=0の時yは最小値を取るので、y=3/8×0²=0
㋑ x=ー3の時yは最大値を取るので、y=3/8×(ー3)²=27/8
②:直線nの式を求める問題です。
n の式を求めなさい。
【・答え y=7/8x+13/4】
点Aと点Cをの座標を求め、直線nの式を求める。
y=3/8×x²にx=ー2を代入し、y=3/8×(ー2)²=3/2
点A(ー2、3/2)
点Bは点Aとy軸に対して線対称なので、点B(2、3/2)
点Bと点Cがx座標が同じなので、y=2x+1にx=2を代入して
y=2×2+1=5
点C(2、5)
点Aと点Cより直線nの傾きは
(5-3/2)/(2-(-2))=7/8
点Cを通るので、切片をcと置くと、
5=7/8×2+c
c=13/4
y=7/8x+13/4
図Ⅱにおいて, p は関数 y =ax2 (a は負の定数) のグラフを表す。 D は m 上の点であり, その x 座標 は正であって, その y 座標は 6 である。E は x 軸上 の点であり,E の x 座標は D の x 座標と等しい。 F は,E を通り y 軸に平行な直線と p との交点で ある。G は,F を通り x 軸に平行な直線とℓとの 交点である。線分 GF の長さは,線分 EF の長さ より 2 cm 長い。a の値を求めなさい。途中の式を 含めた求め方も書くこと。ただし,原点 O から 点( 1 ,0 )まで,原点 O から点( 0 ,1 )までの 距離はそれぞれ 1 cm であるとする。
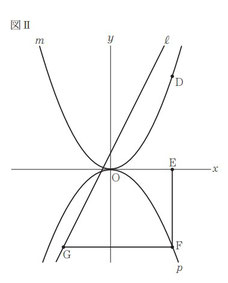
問2:関数Pの傾きaを求める問題です。
【・答え ー5/16】
点D,E,G,Fの座標を求め、線分EF,GFを比較して求める
y=3/8×x²にy=6を代入し、6=3/8×x² →x=4
点A(4,6)
より、点E(4,0)
点Fは点Eとx座標が同じであり、曲線p上にあるので
点E(4、16a)
点Gは点Fとy座標が同じであり、曲線l上にあるので
16a=2×x+1 → x=(16aー1)/2
点G((16aー1)/2、16a)
線分EFは0-16a
線分GFは4-(16aー1)/2 よって、
-16a+2=4-(16aー1)/2
→ a=ー5/16
次の[Ⅰ],[Ⅱ]に答えなさい。
[Ⅰ] 図Ⅰにおいて,△ABC は AB = AC = 8 cm,
BC = 7 cm の 二 等 辺 三 角 形 で あ る。D は,辺 BC 上にあって B,C と異なる点である。A とD とを結ぶ。E は直線 AC について B と反対側にある点であり,3 点 A,C,E を結んでできる
△ACE は △ACE ≡ △BAD で あ る。F は,直線 BC 上にあって C について B と反対側にある点である。A と F とを結ぶ。G は,線分 AF と線分 EC との交点である。
次の問いに答えなさい。
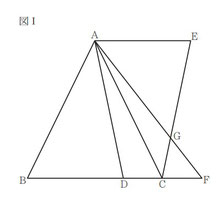
△AEG ∽ △FCG であることを証明しなさい。
【・答え 】
△AEG , △FCGにおいて、
対頂角なので、∠AGE=∠FGC ①
△ACE=△BADより、∠CAE=∠ABD ②
AB=ACより、∠ACB=∠ABD ③
②、③から ∠CAE=∠ACBとなり、錯角が等しくなるので
AE//BFとなる。
平行線の錯角は等しいので、∠AEG=∠FCG ④
①と④から2組の角が等しいので、△AEG ∽ △FCG
FA = FB であり,BD = 5 cm であるときの線分 GF の長さを求めなさい。
【・答え 96/35】
FA=FBより、△ABFは二等辺三角形となるので
∠BAF=∠ABF ①
△ABCはAB=ACの二等辺三角形なので、
∠ABC(=∠ABF)=∠ACB ②
①、②より△ABCと△FABは底角が等しいので
△ABC∽△FABとなる
FA=FB=xとすると
AB:BC=FA:AB
→8:7=x:8
→x=64/7
問1から△AEG ∽ △FCGなので
FG = yとおく
AE:AG=FC:FG
→5:64/7- y = 64/7-7:y
→5y = (64/7- y)(64/7-7)
→(5+15/7)y = 64/7×15/7
→y = 96/35
[Ⅱ] 図Ⅱにおいて, 立体 A-BCD は三角すいであり, 直線 AB は平 面 BCD と 垂 直 で あ る。 △BCD は ∠DBC = 90°の 直 角三角形であり,BC = 8 cm,BD = 6 cm である。E,F,G は,それぞれ辺 AB,AC,AD の中点である。E と F,E と G,F と G とをそれぞれ結ぶ。H は,線分 EB 上にあって E,B と異なる点である。H と C,H と F,H と G とをそれぞれ結ぶ。
I は,H を通り辺 AD に平行な直線と辺 BD との交点である。
I と C とを結ぶ。
次の問いに答えなさい。
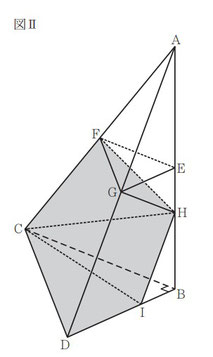
△AFE の面積を S cm2 とするとき,四角形 GDBE の面積を S を用いて表しなさい。
【・答え 9S/4 】
△AEFと△AEGにおいて
面積比は、高さが等しく、底辺の比だけを考えればよいので
△AEF:△AEG = △ACB:△ABD = BC:BD = 8:6
→△AEG = S ×3/4 ①
△AEGと△ABDにおいて
点E,Gなのではそれぞれ辺AB,ADの中点
AE:AB = 1:2
面積比を考えると
△AEG:△ABD= 1²:2²
→ △ABD = △AEG×4 ②
①、②より
△ABD = S ×3/4×4 = 3S
GDBE = △ABD – △AEG
= 3S – S ×3/4
= S×9/4
AB = 12 cm であり,立体 A-BCD から立体 AHFG と立体 HBCI を取り除いてできる立体の体積が 70 cm3 であるときの,線分 HB の長さを求めなさい。
【・答え (3+√21)/2 】
辺HBの長さをxとする
A-BCDの体積を求める
(6×8÷2)×12÷3 = 96 ①
G-AFHの体積を求める
高さを辺EG,底面を△AHF(底辺AH,高さFE)とすると
FE = CB÷2 = 4
EG = BD÷2 = 3
((12-x)×4)÷2)×3÷3 = 24-2x ②
H-BCIの体積を求める
△ABDにおいてHI//ADより、
BH:BA = BI:BD
→ x:12 = BI:6
→ BI= x/2
(x/2×8÷2)×x÷3 = 2x²/3 ③
①、②、③より
96- (24-2x+2x²/3) = 70
→2x²/3-2x+12= 0
→x = (3±√21)/2
BHはEBより小さくなければならないので、
0≦ x ≦6より
x = (3+√21)/2
家庭教師のやる気アシストは、大阪府にお住まいの受験生のお子さんを毎年たくさん指導をさせ頂き、合格に導いています。
おかげさまで、昨年度の合格率は、関西エリア全体で97.3%という結果を残すことが出来ました。
高い合格率の秘訣は、指導経験豊富な先生の指導力に加え、1対1の指導でお子さん一人ひとりの状況に合わせた、お子さんだけのカリキュラムで勉強が進められるから!
家庭教師のやる気アシストは、お子さんの志望校合格まで全力でサポートさせて頂きます!
お子さんにとって「成果が出る勉強法」ってどんな勉強法だと思いますか?
お子さんそれぞれに、個性や性格、学力の差もあります。そんな十人十色のお子さん全員に合う勉強法ってなかなかないんです。
たからこそ、受験生の今だけでもお子さんだけの勉強法で受験を乗り越えてみませんか?
やる気アシストには、決まったカリキュラムはありません。お子さんの希望や学力、得意や不得意に合わせて、お子さんだけのカリキュラムで指導を行っていきます。また、勉強法もお子さんそれぞれに合う合わないがあります。無料体験授業では、お子さんの性格や生活スタイルを見せていただき、お子さんにとって効率的な成果の出る勉強のやり方をご提案させて頂きます。

