







大阪府の2023年3月実施の令和5年度(2023年度)入学者の公立高校入試問題の解説をしています。
受験勉強において、過去問を解くことはとても効果的な勉強法です。ぜひ、受験までに一度挑戦し、問題の傾向を掴んでおきましょう。合わせて、対策などをたてられるととても良いですね。
また、過去問で苦手な点が見つかった場合は、そこを中心に試験日当日までにしっかりと対策しておきましょう。
大阪府の数学問題は、レベル別にABCの問題が用意されています。受験する学校によりどの問題を採用するかが異なります。
難易度は、Aが易、Bがやや難、Cが難となっています。レベル差が顕著なので、各問題に対応する対策をとる必要があります。
次の計算をしなさい。
(1) $6-(-7)$
(2)$\frac{9}{2} \div (-\frac{9}{4})$
(3) $5\times 3^2$
(4) $2(x+y)+x-13y$
(5) $7x^2\times4x$
(6) $5\sqrt{5}-\sqrt{20}$
(1) $13$
$6-(-7)=6+7=13$
(2) $-2$
$\frac{9}{2} \div (-\frac{9}{4})=\frac{9}{2}\times(-\frac{4}{9})=-2$
(3) $45$
$5\times3\times3=45$
(4) $3x-11y$
$2x+2y+x-13y=3x-11y$
(5) $28x^3$
(6) $3\sqrt{5}$
$5\sqrt{5}-\sqrt{4\times5}=5\sqrt{5}-\sqrt{2^2\times5}=5\sqrt{5}-2\sqrt{5}=3\sqrt{5}$
次の問いに答えなさい。
(1) $a=4$のとき、$6a+5$の値を求めなさい。
(2) 次のア~エのうち、無理数であるものはどれですか。一つ選び、記号で答えなさい。
ア:$\frac{1}{3}$ イ:$\sqrt{3}$ ウ:$0.3$ エ:$\sqrt{9}$
(3) 比例式$x:8=5:4$を満たすxの値を求めなさい。
(4) 次のア~エのうち、yがxに反比例するものはどれですか。一つ選び、記号で答えなさい。
ア:1本の値段が100円のペンをx本買った時の代金y円
イ:30枚の色紙からx枚を使ったときの残りの色紙の枚数y円
ウ:1500mの道のりを分速xmで歩いたときにかかる時間y分
エ:xmLのお茶を5人で同じ量に分けたときの一人当たりのお茶の量ymL
(5) 次のデータは6人の生徒それぞれが1学期に読んだ本の冊数を値の小さい順に並べたものである。6人の生徒それぞれが読んだ本の冊数の範囲を求めなさい。
【3 4 4 8 11 15】
(6) 以下の連立方程式を解きなさい。
$2x+3y=11$
$x-3y=10$
(7) 二つの箱A、Bがある。 箱Aには奇数の書いてある3枚のカード 1、3、5が入っており、箱Bには偶数の書いてある3枚のカード 4、6、8が入っている。 A、Bそれぞれの箱から同時にカードを1枚ずつ取り出すとき、 取り出した2枚のカードに書いてある数の和が7である確率はいくらですか。 A, B それぞれの箱において、 どのカードが取り出されることも同様に確からしいものとして答えなさい。
(8) 二次方程式$x^2-8x+12$を解きなさい。
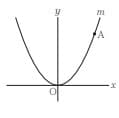
(9) 次の図において、mは関数$y=ax^2$(aは定数)のグラフを表す。Aはm上の点であり、その座標は(5,7)である。aの値を求めなさい。
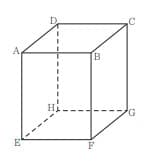
(10) 次の図において、立体ABCD-EFGHは直方体であり、AB=AD=4cm、AE=5cmである。
①次のア~エのうち、辺AEとねじれの位置にある辺はどれですか。一つ選び記号で答えなさい。
ア:辺AB イ:辺BF ウ:辺EH エ:辺FG
②立体ABCD-EFGHの表面積を求めなさい。
(1) $29$
$a=4$を代入すればよいです。
$6a+5=6\times4+5=29$
(2) イ
無理数とは、小数点が永遠に続き、全てを書き表すのが『無理』な数のことです。
$\sqrt{3}=1.7320508…$となり無限に続きます。
エは$\sqrt{9}=3$となるので注意です。
(3) $x=10$
比例式は外掛け=内掛けで解くことができます。
$x\times4=8\times5$
$4x=40$
$x=10$
(4) ウ
それぞれ次のような式で表せます。
ア:$y=100x$
イ:$y=30-x$
ウ:$y=\frac{1500}{x}$
エ:$y=\frac{x}{5}$
これらのうち、反比例の式$y=\frac{a}{x}$に該当するのはウのみです。
(5) $12$
範囲は最大値から最小値を引けばよいので
$15-3=12$
(6) $x=7,y=-1$
加減法で求めます。一つ目の式+二つ目の式で
$3x=21$
$x=7$
一つ目の式に代入して
$2\times7+3y=11$
$3y=-3$
$y=-1$
(7) $\frac{2}{9}$
起こるパターンは$(1,4)(1,6)(1,8)(3,4)(3,6)(3,8)(5,4)(5,6)(5,8)$の9通りです。
このうち、数の和が7となるのは$(1,6)(3,4)$の2通りなので
確率は$\frac{2}{9}$となります。
(8)$x=6,2$
$x^2-8x+12=0$
$(x-6)(x-2)=0$
(9) $a=\frac{7}{25}$
通る点Aの座標をmに代入すれば求まります。
$a\times5^2=7$
$25a=7$
(10) ①エ ②$112cm^2$
①ねじれの位置は平行で交わることがない関係のことです。他にも辺BC,CD,HGが該当します。
②表面積は全ての面積の足し合わせなので
$(4\times4\times2)+(4\times5\times4)=112$
体育祭の準備のため、Fさんはグラウンドで先生と一緒に、杭を打ってロープを張ることになった。ロープは、それぞれの杭の上部にある輪に結びながら張っていく。杭に結ぶロープの長さは全て20cmであり、ロープはたるみなく張るものとする。
Fさんは、杭を100cm感覚で打ってロープを張ることにした。下の図は、Fさんが使ったロープを表す模式図である。「杭の本数」がx本の時の「使ったロープの長さ」をycmとする。x=2のときy=140であるとし、xの値が1増えるごとにyの値は120ずつ増えるものとする。
次の問いに答えなさい。

(1) 次の表は、xとyとの関係を示した表の一部である。表中の(ア)(イ)に当てはまる数をそれぞれ書きなさい。
| x | 2 | 3 | 4 | ・・・ | 7 | ・・・ |
| y | 140 | 260 | (ア) | ・・・ | (イ) | ・・・ |
(2) xを2以上の自然数として、yをxの式で表しなさい。
(3)y=1580となるときのxの値を求めなさい。
(1) (ア)380 (イ)740
1本打つごとに120cmずつ増えていることに注目します。
(2) $y=120x-100$
$y=140+120(x-2)$の法則を読み取ります。
(3) $x=14$
前問で求めた式に代入します。
$1580=120x-100$
次の図において、△ABCは∠ABC=90°の直角三角形であり、AB=3cmである。Dは、辺AC上にあって、A,Cと異なる点である。△EDB≡△ADBであり、DE//BCである。Fは、辺EBと辺ACとの交点である。BC=xcmとし、x>0とする。
次の問いに答えなさい。
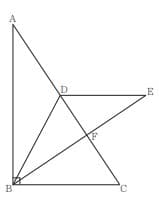
(1) △ADBを、ある直線を対称の軸として対象移動すると、△EDBにぴったり重ねることができる。次のア~エの直線のうち、このときの対象の軸はどれですか。一つ選び、記号を答えなさい。
ア:直線DB イ:直線AB ウ:直線AC エ:直線DE
(2) △ABCの面積をxを用いて表しなさい。
(3) 次は、△ABC∽△BFCであることの証明である。【 a 】、【 b 】に入れるのに適している「角を表す文字」をそれぞれ書きなさい。また、c[ ]に適しているものを一つ選び、記号を答えなさい。。
(証明)
△ABCと△BFCにおいて
∠ACB=∠【 a 】(共通)…①
△ADB≡△EDBだから、∠CAB=∠DEB…②
DE//BCであり、平行線の錯角は等しいから
∠【 b 】=∠DEB…③
②、③より、∠CAB=∠【 b 】…④
①、②より
c[
ア 1組の辺とその両端の角
イ 2組の辺の比とその間の角
ウ 2組の角
]
がそれぞれ等しいから、
△ABC∽△BFC
(4) x=2であるときの線分BFの長さを求めなさい。答えを求める過程がわかるように、途中の式を含めた求め方も説明すること。
(1) ア
対象の軸で折るとぴったり重なるので、答えは辺BDとなります。
(2) $\frac{3}{2}x(cm^2)$
三角形の面積なので
$x\times3\div2$で求まります。
(3)【 a 】→BCF 【 b 】→CBF c→ウ
(4) $\frac{6\sqrt{13}}{13}(cm)$
∠ABC=90°なので、AB²+BC²=AC²
AC=ycmとすると、3²+2²=y²
これを解くと、y>0より$y=\sqrt{13}$
△ABC∽△BFCだから
$AB:BF=AC:BC=\sqrt{13}:2$
よって、$BF=\frac{2}{\sqrt{13}}AB=\frac{6\sqrt{13}}{13}$
次の計算をしなさい。
(1) $6\times(-1)-3^2$
(2) $4(5a+2b)-7(2a+b)$
(3) $24x^2\div 3xy \times (-\frac{1}{2}y^2)$
(4) $x(x+10)-(x+3)(x-1)$
(5) $(2\sqrt{7}+\sqrt{2})(2\sqrt{7}-\sqrt{2})$
(1)$-15$
$-6-9=-15$
(2) $6a+b$
$20a+8b-14a-7b=6a+b$
(3) $-4xy$
$24x^3 \times \frac{1}{3xy} \times (-\frac{1}{2}y^2)$
(4) $8x+3$
$x^2+10x-(x^2+2x-3)=8x+3$
(5) $26$
$(2\sqrt{7})^2-(\sqrt{2}^2)=28-2=26$
(1) a=4、b=-5のとき、a²-3bの値を求めなさい。
(2) 二次方程式x²+x-42=0を解きなさい。
(3) $3<\sqrt{n}<3\sqrt{2}$を満たす自然数nの個数を求めなさい。
(4) 関数$y=ax^2$(aは定数)について、xの値が-1から5まで増加するときの変化の割合が16であるとき、aの値を求めなさい。
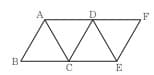
(5) 次の図は、正四面体の展開図である。次の展開図を組み立てて正四面体をつくったとき、次のア~オのうち、辺ABとねじれの位置にある辺はどれですか。一つ選び、記号を答えなさい。
ア:辺CD イ:辺CE ウ:辺DE エ:辺DF オ:辺EF
(6) A,Bふたつのさいころを同時に投げ、Aのさいころの出る目の数をa、Bのさいころの出る目の数をbとするとき、2a+bの値が5の倍数である確率はいくらですか。1から6までのどの目が出ることも同様に確からしいものとして答えなさい。
(7) 次のデータは、9人の生徒のそれぞれが1学期に読んだ本の冊数を示したものである。9人の生徒がそれぞれ読んだ本の冊数の中央値が8冊であり、四分位範囲が6冊であるとき、データの中のxの値を求めなさい。
【3 9 x 4 15 5 8 4 9】
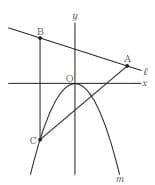
(8) 次の図において、mは関数$y=ax^2$(aは負の定数)のグラフを表し、lは関数$y=-\frac{1}{3}x+2$のグラフを表す。A,Bはl上の点であって、Aのy座標は1であり、Bのx座標は-2である。Cは、Bを通りy軸に平行な直線とmとの交点である。CとAとを結ぶ。△ABCの面積は15㎠である。aの値を求めなさい。答えを求める過程がわかるように、途中の式を含めた求め方も説明すること。ただし、原点Oから点(1,0)までの距離、原点Oから点(0,1)までの距離はそれぞれ1㎝であるとする。
(1) $31$
$4^2-3\times(-5)=16+15=31$
(2) $x=-7,6$
$x^2+x-42=0$
$(x+7)(x-6)=0$
(3) 8個
全体を2乗すると
$9<n<18$となるので、あてはまるnの数は$n=10,11,12,13,14,15,16,17$となる。
(4) $a=4$
変化の割合はyの増加量/xの増加量で求まるので
$\frac{25a-a}{5-(-1)}=16$
$4a=16$
(5) ア
ねじれの位置は平行で交わることがない関係のことです。
(6) $\frac{7}{36}$
まず全通りを考えると$6\times6=36$通り。
次にaの目が出たときに2a+bが5の倍数となるbの値を求めると
$(a,b)=(1,3)(2,1)(2,6)(3,4)(4,2)(5,5)(6,3)$の7通りです。
※5の倍数は一の位の数が「5」か「0」になるのがポイントです。
よって、確率は$\frac{7}{36}$となります。
(7) $x=11$
中央値が8ということは5番目の数が8となるということ。
四分位範囲が6になるということはQ3(第三四分位数)からQ1(第一四分位数)を引いた数が6となるということです。
中央値の条件からx以外の数を小さい順に並べると5番目の数は8なので、xは8以上であることが分かります。
さらに、Q1=【3,4,4,5】の中央値=4から、Q3は10になることが分かります。
つまり、$(x+9)\div2=10$が成り立つ必要があるので、$x=11$と分かります。
(8) $a=-\frac{5}{6}$
A、B、Cそれぞれの座標を求めます。
Aのx座標はlにy=1を代入して、 $x=3$ よって、$A(3,1)$
Bのx座標は-2。これをlに代入して、 $y=\frac{8}{3}$よって、$B(-2,\frac{8}{3})$
Cはx座標がBとおなじなので、mに代入して$C(-2,4a)$
よって、$(\frac{8}{3}-4a)\times(2+3)\div2=15$となるので
$a=-\frac{5}{6}$
体育祭の準備のため、FさんとGさんはどれぞれグラウンドで先生と一緒に、杭を打ってロープを張ることになった。ロープは、それぞれの杭の上部にある輪に結びながら張っていく。杭に結ぶロープの長さは全て20cmであり、ロープはたるみなく張るものとする。
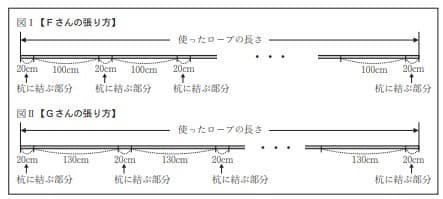
Fさんは、杭を100cm間隔で打ってロープを張ることにした。図Ⅰは、Fさんが使ったロープを表す模式図である。 「杭の本数」が2本のとき「使ったロープの長さ」は140cmであるとし、 「杭の本数」が1本増えるごとに「使ったロープの長さ」は120cmずつ長くなるものとする。(これを【Fさんの張り方】 とする。)
Gさんは、 杭を130cm間隔で打ってロープを張ることにした。 図Ⅱは、 Gさんが使ったロープを表す模式図である。 「杭の本数」が2本のとき「使ったロープの長さ」 は170cmであるとし、 「杭の本数」が1本増えるごとに「使ったロープの長さ」 は150cmずつ長くなるものとする。 (これを 【Gさんの張り方】 とする。)
次の問いに答えなさい。
(1) 【Fさんの張り方】において、「杭の本数」がx本のときの「使ったロープの長さ」をycmとする。
①次の表は、xとyの関係を示した表の一部であ(1) 次の表は、xとyとの関係を示した表の一部である。表中の(ア)(イ)に当てはまる数をそれぞれ書きなさい。
| x | 2 | 3 | 4 | ・・・ | 7 | ・・・ |
| y | 140 | 260 | (ア) | ・・・ | (イ) | ・・・ |
(2) xを2以上の自然数として、yをxの式で表しなさい。
(3)y=1580となるときのxの値を求めなさい。
(2) Fさんは【Fさんの張り方】でs本の杭を打ってロープを張り、Gさんは【Gさんの張り方】でt本の杭を打ってロープを張った。2人が打った杭の本数の合計が38本であり、Fさんが使ったロープの長さとGさんが使ったロープの長さが同じであるとき、s,tの値をそれぞれ求めなさい。
(1)① (ア)380 (イ)740
1本打つごとに120cmずつ増えていることに注目します。
➁$y=120x-100$
$y=140+120(x-2)$の法則を読み取ります。
➂ $x=14$
前問で求めた式に代入します。
$1580=120x-100$
(2) $s=21,t=17$
Gさんの張り方の場合に、yをxの式で表すと$y=150x-130$となります。
ここでsとtについて次の連立方程式が成り立ちます。
2人が打った杭の本数の合計が38本なので、 s+t=38・・・①
ロープの長さが同じになったことから、 120s-100=150t-130・・・②
これらを解くと、$s=21,t=17$
次の[Ⅰ]、[Ⅱ]に答えなさい。
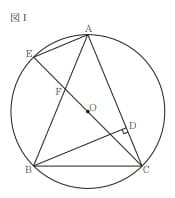
[Ⅰ]図Ⅰにおいて、A、B、Cは点Oを中心とする円の周上の異なる3点である。 3点A、B、Cを結んでできる△ABCはAB=ACの二等辺三角形であり、頂角∠BACは鋭角である。 D は、Bから線分ACにひいた垂線と線分ACとの交点である。 Eは、 直線 OC と円Oとの交点のうちCと異なる点である。 Fは、線分 EC と線分ABとの交点である。EとAとを結ぶ。
次の問いに答えなさい。
(1) △EAC∽△CDBであることを証明しなさい。
(2) AD=5㎝、BG=2㎝であるとき、
①辺BDの長さを求めなさい。
②線分AFの長さを求めなさい。
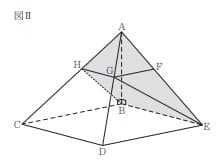
[Ⅱ]図Ⅱにおいて、立体 ABCDE は四角すいであり、 直線AB は平面 BCDEと垂直である。AB=3cmである。 四角形BCDE は長方形であり、 BC = 5cm、BE=4cmである。 Fは、辺AE上の点である。 Gは、Fを通り辺 DE に平行な直線と辺AD との交点である。 GとEとを結ぶ。 Hは、Gを通り辺 CD に平行な直線と辺 AC との交点である。 HとBとを結ぶ。
このとき、4点H、G、E、Bは同じ平面上にある。
次の問いに答えなさい。
(3) 次のア〜エのうち、その大きさが90°であるものはどれですか。一つ選び、記号を答えなさい。
ア:△ACDの内角∠ACD イ:△ACDの内角∠ADC ウ:△ADEの内角∠ADE エ:△ADEの内角∠AED
(4) FE=3cmであるとき、
①△HCBの面積を求めなさい。
②立体AHGEBの体積を求めなさい。
[Ⅰ]
(1)
△EACと△CDBにおいて
半円の弧に対する円周角は90°なので
∠EAC=90°…①
BD⊥ACだから、∠CDB=90°…②
①、➁より∠EAC=∠CDB…③
同じ弧に対する円周角は等しいから
∠AEC=∠ABC…④
△ABCはAB=ACの二等辺三角形だから
∠DCB=∠ABC…⑤
➃、⑤より∠AEC=∠DCB…⑥
➂、⑥より、2組の角がそれぞれ等しいから
△EAC∽△CDB
(2)
① $2\sqrt{6}cm$
△ABCは二等辺三角形なのでAB=AC=7cm
△ABDに注目すると、三平方の定理より$5^+AD^2=7^2$
よって、$AD^2=24$
② $frac{49}{17}cm$
AFの長さを求めるためには、AF:FBの比が分かれば求まります。
つまり、△EAC:△EBCの面積比を求めればよいことになります。
△EAC:△CDB=AC²:DB²=49:24
△EAC∽△GDCより、△EAC:△GDC=AC²:DC²=49:4
△GBC=24-4=20
△EBG:△GBC=EG:GC=AD:DC=5:2
△EBC=$20\times\frac{7}{2}=70
よって、AF:FB=△EAC:△EBC=49:70=7:10
$AF=7\times\frac{7}{17}=\frac{49}{17}
[Ⅱ]
(3) ア、エ
(4) ①$\frac{9}{2}cm^2$
△ABEは3:4:5の直角三角形なので、AE=5cm
平行線の性質より、AF:FE=AG:GD=AH:HC=2:3
$△HCB=△ACB\times\frac{3}{5}=\frac{9}{2}$
② $\frac{28}{5}cm^3$
$△AHB=\frac{9}{2}\times\frac{2}{3}=3$
これを底面とする立体で堆積を求めます。
△AHG∽△ACDより、$HG=4\times\frac{2}{5}=\frac{8}{5}cm$
高さはA,HG,BEの平均なので
立体の体積は$3\times(0+\frac{8}{5}+4)\div3=\frac{28}{5}$
家庭教師のやる気アシストは、大阪府にお住まいの受験生のお子さんを毎年たくさん指導をさせ頂き、合格に導いています。
高い合格率の秘訣は、指導経験豊富な先生の指導力に加え、1対1の指導でお子さん一人ひとりの状況に合わせた、お子さんだけのカリキュラムで勉強が進められるから!
家庭教師のやる気アシストは、お子さんの志望校合格まで全力でサポートさせて頂きます!
お子さんにとって「成果が出る勉強法」ってどんな勉強法だと思いますか?
お子さんそれぞれに、個性や性格、学力の差もあります。そんな十人十色のお子さん全員に合う勉強法ってなかなかないんです。
たからこそ、受験生の今だけでもお子さんだけの勉強法で受験を乗り越えてみませんか?
やる気アシストには、決まったカリキュラムはありません。お子さんの希望や学力、得意や不得意に合わせて、お子さんだけのカリキュラムで指導を行っていきます。また、勉強法もお子さんそれぞれに合う合わないがあります。無料体験授業では、お子さんの性格や生活スタイルを見せていただき、お子さんにとって効率的な成果の出る勉強のやり方をご提案させて頂きます。

