







東京都の2024年3月実施の令和6年度(2024年度)入学者の公立高校入試問題の解説をしています。
受験勉強において、過去問を解くことはとても効果的な勉強法です。ぜひ、受験までに一度挑戦し、問題の傾向を掴んでおきましょう。合わせて、対策などをたてられるととても良いですね。
また、過去問で苦手な点が見つかった場合は、そこを中心に試験日当日までにしっかりと対策しておきましょう。
次の各問いに答えよ。
\(-6^2 × \displaystyle \frac{1}{9} -4\) を計算せよ。
\(2a+b-\displaystyle \frac{5a-b}{3}\) を計算せよ。
\((\sqrt{7}-1)(2\sqrt{7}+6)\) を計算せよ。
一次方程式 \(2x-8 = -x+4\) を解け。
連立方程式 \(\displaystyle \begin{cases} 5x + 7y = 9 \\ 3x + 4y = 6 \end{cases}\) を解け。
二次方程式\( (x-8)^2 = 1\) を解け。
右の図1は,ある中学校第2学年の,A組,B組,C組それぞれ生徒37人のハンドボール投げの記録を箱ひげ図に表したものである。
図1から読み取れることとして正しいものを,次のア〜エのうちから選び,記号で答えよ。
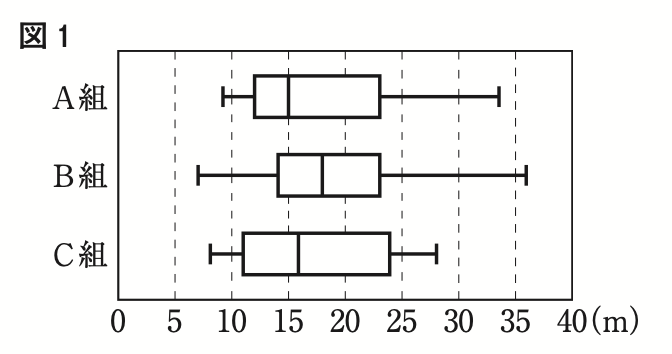
ア A組,B組,C組のいずれの組にも,記録が30m を上回った生徒がいる。
イ A組,B組,C組の中で,最も遠くまで投げた生徒がいる組はC組である。
ウ A組,B組,C組のいずれの組にも,記録が 15m の生徒はいない。
エ A組,B組,C組の中で,四分位範囲が最も小さいのはB組である。
次の[ ]の中の「あ」「い」に当てはまる数字をそれぞれ答えよ。
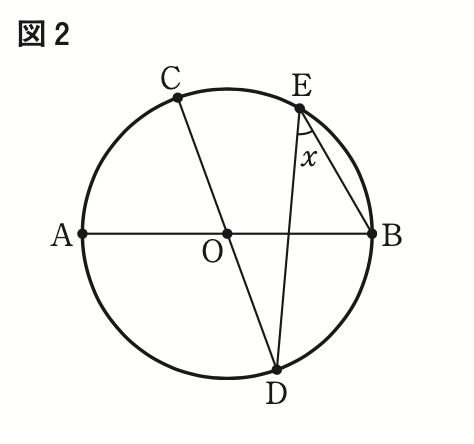
右の図2で,点Oは,線分ABを直径とする円の中心であり,3点C,D,Eは円Oの周上にある点である。
5点A,B,C,D,Eは,右の図 2 のように,A,D,B,E,Cの順に並んでおり,互いに一致しない。
点Bと点E,点Cと点D,点Dと点Eをそれぞれ結ぶ。
線分CDが円Oの直径,\(\stackrel{\frown}{AC}\)=\(\displaystyle \frac{2}{5}\)\(\stackrel{\frown}{AB}\)のとき,xで示した∠BEDの大きさは,[あい]度である。
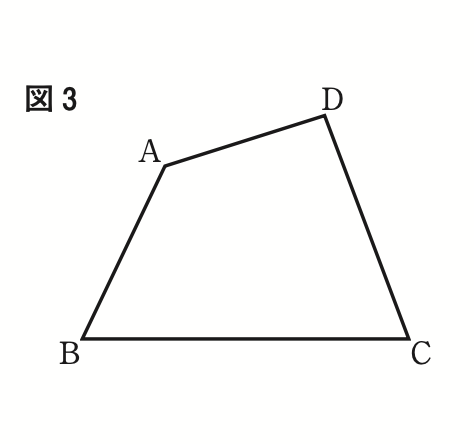
右の図 3 で,四角形ABCDは,∠BADが鈍角の四角形である。
解答欄に示した図をもとにして,四角形ABCDの辺上にあり,辺ABと辺ADまでの距離が等しい点Pを,定規とコンパスを用いて作図によって求め,点Pの位置を示す文字Pも書け。
ただし,作図に用いた線は消さないでおくこと。
計算の順序を間違えないようにしましょう。
$-6\times6\times\frac{1}{9}-4=-4-4=-8$
通分をしてから求めます。
$\frac{3(2a+b)-(5a+b)}{3}=\frac{6a+3b-5a-b}{3}$
展開をして求めます。
$7+6\sqrt{7}-\sqrt{7}-6=1+5\sqrt{7}$
$3x=12$
$x=4$
1つ目の式に4を掛け、2つ目の式に7を掛けて、加減法で求めます。
平方根の解き方を行います。
$(x-8)=\pm\sqrt{1}$
$x=7,9$
ア:C組には30mを上回った生徒はいません。
イ:最も遠くまで投げた生徒がいるのはB組です。
ウ:A組に15mの生徒がいるので不適です。
まず、弧ACは2/5弧ABとあり、弧ABは半径なので、中心角は180°です。
よって。$∠AOC=180\times\frac{2}{5}=72°$です。
対頂角は等しいので、∠BOD=∠AOC=72°
∠BEDは∠BODの円周角なので、$∠BED=\frac{1}{2}∠BOD=36°$
Sさんのクラスでは、先生が示した問題をみんなで考えた。次の各問に答えよ。
[先生が示した問題]
a,b を正の数とする。
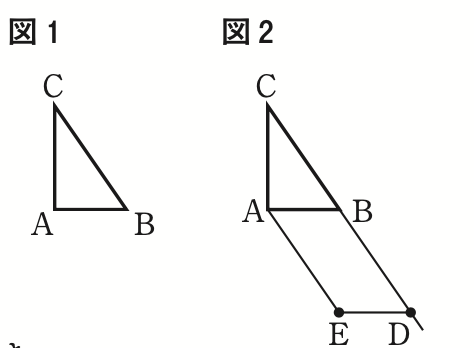
右の図 1 で,△ABCは,∠BAC=90°,AB= a cm,AC= b cm の直角三角形である。
右の図 2 に示した四角形AEDCは,図 1 において,辺BCをBの方向に延ばした直線上にありBC=BDとなる点をDとし,△ABCを頂点Bが点Dに一致するように平行移動させたとき,頂点Aが移動した点をEとし,頂点Aと点E,点Dと点Eをそれぞれ結んでできた台形である。
四角形AEDCの面積は,△ABCの面積の何倍か求めなさい。
次の[ ]の中の「う」に当てはまる数字を答えよ。
[先生が示した問題]で,四角形AEDCの面積は,△ABCの面積の[う ]倍である。
Sさんのグループは、[先生が示した問題]をもとにして、次の問題を作った。
[Sさんのグループが作った問題]
a,b,x を正の数とする。
右の図 3 に示した四角形AGHCは,図 1 において,辺ABをBの方向に延ばした直線上にある点をFとし,△ABCを頂点Aが点Fに一致するように平行移動させたとき,頂点Bが移動した点をG,頂点Cが移動した点をHとし,頂点Cと点H,点Gと点Hをそれぞれ結んでできた台形である。
右の図 4 に示した四角形ABJKは,図 1 において,辺ACをCの方向に延ばした直線上にある点をIとし,△ABCを頂点Aが点Iに一致するように平行移動させたとき,頂点Bが移動した点をJ,頂点Cが移動した点をKとし,頂点Bと点J,点Jと点Kをそれぞれ結んでできた台形である。
図 3 において,線分AFの長さが辺ABの長さの x 倍となるときの四角形AGHCの面積と,図 4 において,線分AIの長さが辺ACの長さの x 倍となるときの四角形ABJKの面積が等しくなることを確かめてみよう。
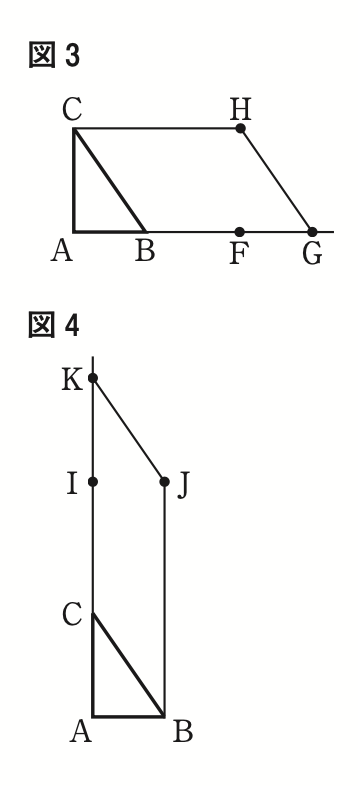
[Sさんのグループが作った問題]で,四角形AGHCの面積と四角形ABJKの面積を,それぞれ a,b,x を用いた式で表し,四角形AGHCの面積と四角形ABJKの面積が等しくなることを証明せよ。
BEを結ぶと△ABC≡△ABE≡△EDBだとわかるので、3倍となります。
四角形AGHCは、上底がaxcm,下底が(ax+a)cm,高さがbcmの台形下底が(ax+a)cm,高さがbcmの台形だから、四角形AGHCの面積は
${ax+(ax+a)}\times b\times\frac{1}{2}=\frac{1}{2}ab(2x+1)$…➀
四角形ABJKは、上底がbxcm,下底が(bx+b)cm,高さがacmの台形だから、四角形ABJKの面積は
${bx+(bx+b)}\times a\times\frac{1}{2}=\frac{1}{2}ab(2x+1)$…②
➀、 ➁より、四角形AGHCの面積と四角形ABJKの面積は等しい。
右の図1で、点Oは原点、曲線lは関数 \(\displaystyle y = \frac{1}{4}x^2 \) のグラフを表している。
点Aは曲線 l 上にあり,x 座標は-6である。曲線 l 上にある点をPとする。
次の各問に答えよ。
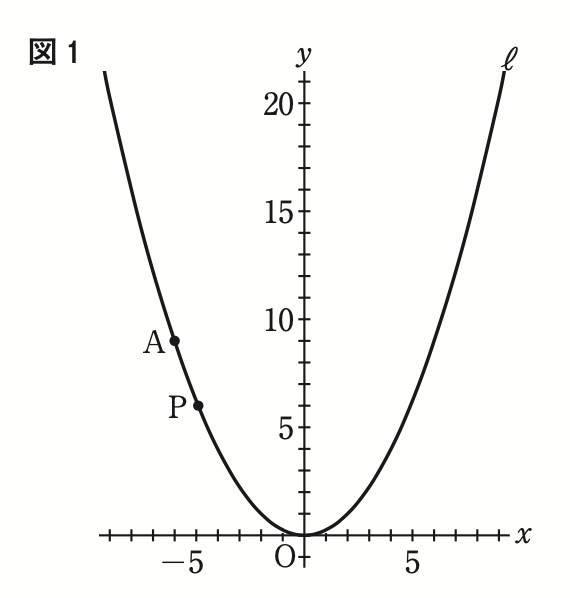
次の[①]と[②]に当てはまる数を,下のア〜クのうちからそれぞれ選び,記号で答えよ。
点Pの x 座標を a,y 座標を b とする。
a のとる値の範囲が−3≦ a ≦1のとき,b のとる値の範囲は,
[①]≦ b ≦ [②]
である。
ア \(-\displaystyle\frac{9}{4}\)
イ \(-\displaystyle\frac{3}{2}\)
ウ \(-\displaystyle\frac{3}{4}\)
エ \(0\)
オ \(\displaystyle\frac{1}{4}\)
カ \(\displaystyle\frac{1}{2}\)
キ \(\displaystyle\frac{3}{2}\)
ク \(\displaystyle\frac{9}{4}\)
次の[③]と[④]に当てはまる数を,下のア〜エのうちからそれぞれ選び,記号で答えよ。
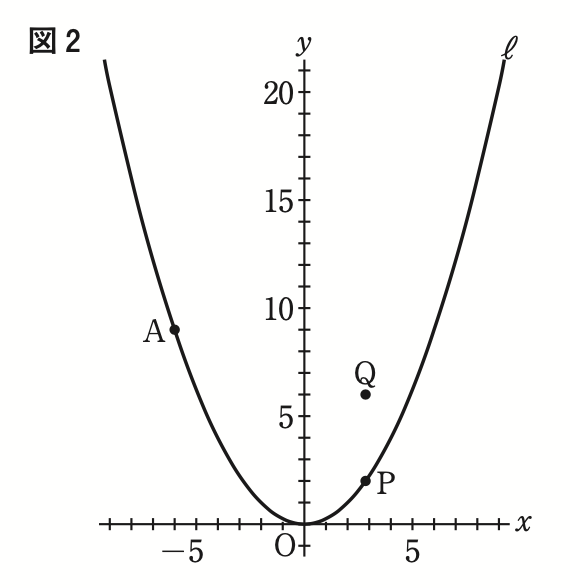
右の図 2 は,図 1 において,x 座標が点Pの x 座標と等しく,y 座標が点Pの y 座標より4大きい点をQとした場合を表している。
点Pの x 座標が2のとき,2点A,Qを通る直線の式は,
y= [③] x + [④]
である。
ア \(2\)
イ \(\displaystyle\frac{1}{2}\)
ウ \(-\displaystyle\frac{1}{2}\)
エ \(-2\)
ア \(6\)
イ \(5\)
ウ \(4\)
エ \(1\)
図 2 において,点Pの x 座標が3より大きい数であるとき,点Qを通り傾き\(\displaystyle\frac{1}{2}\)の直線を引き,y 軸との交点をRとし,点Oと点A,点Aと点R,点Pと点Q,点Pと点Rをそれぞれ結んだ場合を考える。
△AORの面積が△PQRの面積の3倍になるとき,点Pの x 座標を求めよ。
aの範囲が原点をまたぐので、bの最小値は0だと分かります。
また、最大値は絶対値の大きい方になるので、$b=\frac{1}{4}\times(-3)^2\frac{9}{4}=$
となります。
2点A,Qの座標を求めて連立方程式を解くことで求めることができます。
点Aはx=-6を通るので、$y=\frac{1}{4}\times(-6)^2=9$よって、点A(-6,9)です。
点Qはx=2であり、y座標は点Pよりも4大きいとしているので、点Pの座標は(2,1)より、点Q(2,5)です。
これらをy=ax+bに代入してとくと、(a,b)=(-1/2,6)となるので、式は$y=-\frac{1}{2}x+6$となります。
求めるべきPのx座標をtとすると、点Pと点Qは
$P(t,\frac{1}{4}t^2) Q(t,\frac{1}{4}t^2+4)$と表せるので、
△PQRの面積は2t、△AORの面積は6tです。
よって、RO=2tと分かります。
Rから右へ垂線を引いて足をSとします。
QRの傾きは1/2、よって、QS=1/2t
Qのy座標は、2t+1/2t=5/2tです。
Qのy座標で方程式を立てると
$\frac{1}{4}t^2+4=\frac{5}{2}t$
$t^2-10t+16=0$
$(t-2)(t-8)=0$
t>3なので、$t=8$となります。
右の図1で,四角形ABCDは,AB<ADの長方形である。
辺BCの中点をMとする。
点Pは,線分CM上にある点で,頂点C,点Mのいずれにも一致しない。
頂点Aと点Mを結び,点Pを通り線分AMに平行な直線を引き,辺ADとの交点をQとする。
点Mと点Qを結ぶ。
次の各問に答えよ。
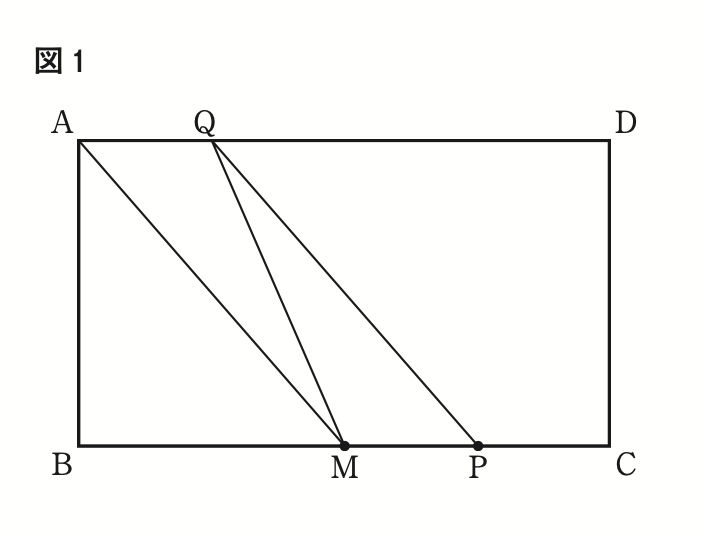
図 1 において,AB=BM,∠AQM= a °とするとき,∠MQPの大きさを表す式を,次のア〜エのうちから選び,記号で答えよ。
ア (180 – a)度
イ (135 – a)度
ウ (a – 90)度
エ (a – 45)度
右の図2は、図1において、頂点Bと頂点Dを結び,線分BDと,線分AM,線分MQ,線分PQとの交点をそれぞれR,S,Tとした場合を表している。
次の①、②に答えよ。
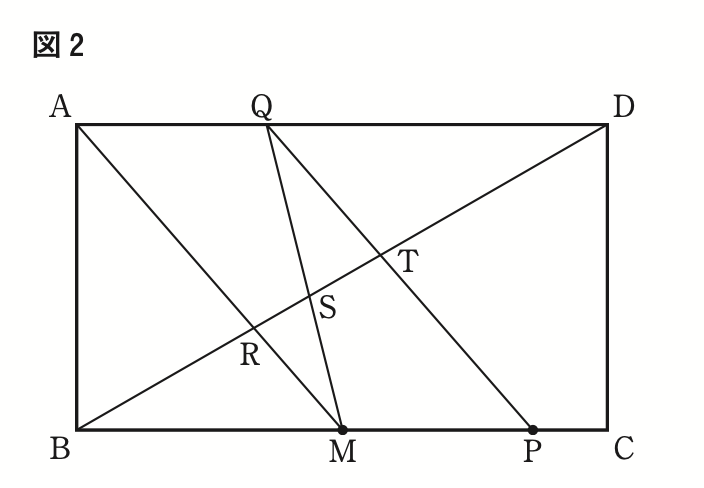
① △BMR ∽ △DQT であることを証明せよ。
② 次のの中の「う」「 え」に当てはまる数字をそれぞれ答えよ。図2において、線分ARと線分BQとの交点をS、点Oと点Rを結び、
線分BQと線分ORとの交点をTとした場合を考える。AP=2OPのとき,△RSTの面積は,四角形AORQの面積の
次の[ ]の中の「え」「お」「か」に当てはまる数字をそれぞれ答えよ。
図 2 において,MP:PC= 3:1のとき,線分STの長さと線分BDの長さの比を最も簡単な整数の比で表すと,ST:BD=[え]: [おか] である。
AB=BM、∠ABM=90°より、△ABMは直角二等辺三角形だと分かるので
∠BAM=∠MAQ=45°
AM//QPの同位角で、∠PQD=a
∠MQP=180-(45+a)=135-aが答えとなります。
①
△BMRと△DQTにおいて
BM//QDより、平行線の錯角は等しいので
∠MBR=∠QDT…➀
対頂角は等しいので
∠BRM=∠DRA…②
AM//QPより、平行線の同位角は等しいので
∠DRA=∠DTQ…③
➁、➂より
∠BRM=∠DTQ…④
➀、➃より、2組の角がそれぞれ等しいので
△BMR∽△DQT
②
MP:PC=3:1
MはBCの中点なので、BM=4
平行四角形AMPQの大変からAQ=3、QD=5
△BMR∽△DQTから、RM:TQ=4:5
△SRM∽△STQより、RS:ST=4:5
△ARD∽△QTDより、RD=$9\times\frac{8}{3}=24$
△ARD∽△MBRより、BD=$24\times\frac{12}{8}=36$
これらより、ST:BD=5:36
右の図に示した立体ABC-DEFは,
AB=AD=6cm,AC=BC=5cm,
∠BAD=∠CAD=90°の三角柱である。
辺CF上にあり,頂点C,頂点Fのいずれにも一致しない点をPとする。
次の各問に答えよ。
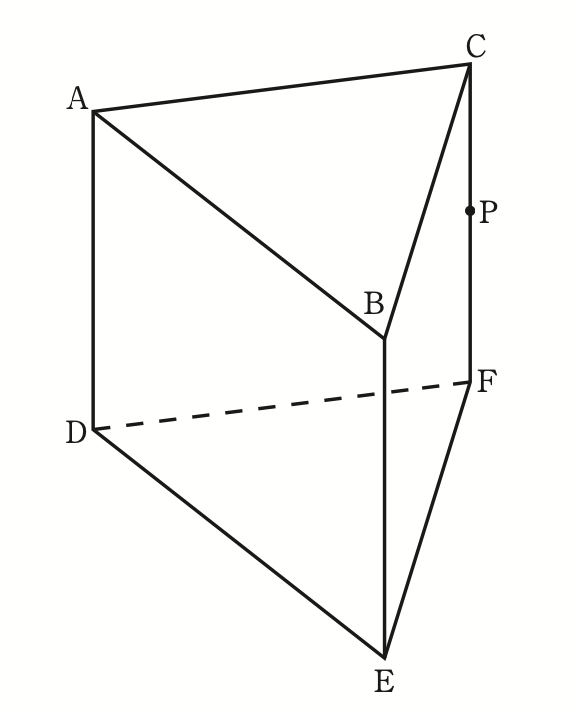
次の[ ]の中の「き」「く」に当てはまる数字をそれぞれ答えよ。
線分ABの中点をMとし,点Mと点Pを結んだ場合を考える。
∠BMPの大きさは,[きく]度である。
次の の中の「け」「こ」に当てはまる数字をそれぞれ答えよ。
頂点Aと点P,頂点Bと点P,頂点Dと点P,頂点Eと点Pをそれぞれ結んだ場合を考える。
立体P-ADEBの体積は,[けこ]cm³である。
△ABCは二等辺三角形です。
Mは底辺ABの中点なので、AB⊥CM
Mの真下をNとすると、BM⊥面MNFC
Pは面MNFC上の点なので、∠BMP=90°です。
CF//面ADEBより、P-ADEBをC-ADEBに等積変形します。
△AMCが3:4:5の直角三角形でCM=4cm
C-ADEBの体積は、底面ADEB×高さCM÷3
$6\times6\times4\div3=48cm^3$
家庭教師のやる気アシストは、東京都にお住まいの受験生のお子さんを毎年たくさん指導をさせ頂き、合格に導いています。
高い合格率の秘訣は、指導経験豊富な先生の指導力に加え、1対1の指導でお子さん一人ひとりの状況に合わせた、お子さんだけのカリキュラムで勉強が進められるから!
家庭教師のやる気アシストは、お子さんの志望校合格まで全力でサポートさせて頂きます!
お子さんにとって「成果が出る勉強法」ってどんな勉強法だと思いますか?
お子さんそれぞれに、個性や性格、学力の差もあります。そんな十人十色のお子さん全員に合う勉強法ってなかなかないんです。
たからこそ、受験生の今だけでもお子さんだけの勉強法で受験を乗り越えてみませんか?
やる気アシストには、決まったカリキュラムはありません。お子さんの希望や学力、得意や不得意に合わせて、お子さんだけのカリキュラムで指導を行っていきます。また、勉強法もお子さんそれぞれに合う合わないがあります。無料体験授業では、お子さんの性格や生活スタイルを見せていただき、お子さんにとって効率的な成果の出る勉強のやり方をご提案させて頂きます。

