【東京都】令和7年度/2025年度入学者高校入試選抜試験：数学の解説
東京都の2025年3月実施の令和7年度（2025年度）入学者の公立高校入試問題の解説をしています。
受験勉強において、過去問を解くことはとても効果的な勉強法です。ぜひ、受験までに一度挑戦し、問題の傾向を掴んでおきましょう。合わせて、対策などをたてられるととても良いですね。
また、過去問で苦手な点が見つかった場合は、そこを中心に試験日当日までにしっかりと対策しておきましょう。
大問1 小問集合
問題文
次の各問いに答えよ。
問1
\(3 – 6^2 \div 4\) を計算せよ。
問2
\(\displaystyle \frac{9a-b}{5} – a + 2b\) を計算せよ。
問3
\((3\sqrt{7}+8)(3\sqrt{7}-8)\) を計算せよ。
問4
一次方程式 \(\displaystyle \frac{9x-6}{2} = 4x+1\) を解け。
問5
連立方程式 \(\displaystyle \begin{cases} 8x – 5y = -3 \\ y = 2x – 1 \end{cases}\) を解け。
問6
二次方程式\(x^2 – 9x + 7 = 0\) を解け。
問7
〔問７〕次の ① と ② に当てはまる数を、下のア～クのうちからそれぞれ選び、記号で答えよ。
関数 \(y = -x^2\) について、\(x\) の変域が \(-2 \leqq x \leqq 3\) のときの \(y\) の変域は、
① \(\leqq y \leqq\) ②
である。
ア -9 イ -6 ウ -4 エ -2
オ 0 カ 4 キ 6 ク 9
問8
次の[ ]の中の「あ」「い」に当てはまる数字をそれぞれ答えよ。
右の図1のように、1,2,3,4,5の数字を1つずつ書いた5枚のカードがある。
この5枚のカードから同時に3枚のカードを取り出すとき，取り出した3枚のカードに書いてある数の和が10以上になる確率は
\(\displaystyle \frac{あ}{い}\)
である。ただし，どのカードが取り出されることも同様に確からしいものとする。
問9
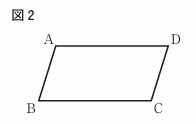
右の図2で、四角形ＡＢＣＤは平行四辺形である。解答欄に示した図をもとにして、辺ＡＤ上にあり、頂点Ｂ、頂点Ｃまでの距離が等しい点Ｐを、定規とコンパスを用いて作図によって求め、
点Ｐの位置を示す文字Ｐも書け。
ただし、作図に用いた線は消さないでおくこと。
解答・解説
問1 $-6$
計算の順序を間違えないようにしましょう。
$3-36\div4=3-9=-6$
問2 $\frac{4a+9b}{5}$
通分をしてから求めます。
$\frac{9a-b-5a+10b}{5}=\frac{4a+9b}{5}$
問3 $-1$
$(x+a)(x-a)=x^2-a^2$を用います。
$(3\sqrt{7}+8)(3\sqrt{7}-8)=(3\sqrt{7})^2-8^2=63-64=-1$
問4 $x=8$
両辺に2を掛けて、分数を取り除きましょう。
$9x-6=8x+2$
$x=8$
問5 $x=4,y=7$
2つ目の式を1つ目の式に代入します。
$8x-5(2x-1)=-3$
$-2x=-8$
$x=4$
これを2つ目の式に代入します。
$y=2\times4-1=7$
問6 $\frac{9 \pm \sqrt{53}}{2}$
解の公式$x=\frac{-b \pm \sqrt{b^2-4ac}}{2a}$を用います。
$x=\frac{-(-9) \pm \sqrt{(-9)^2-4\times1\times7}}{2\times1}=\frac{9 \pm \sqrt{53}}{2}$
問7 ①ア ②オ
上に凸の二次関数なので、yの最大値は0をとり、最小値は絶対値が大きい方のｘの値を代入すればよいです。
問8 $\frac{2}{5}$
まず全通りを考えると
$(1,2,3)(1,2,4)(1,2,5)(1,3,4)(1,3,5)(1,4,5)(2,3,4)(2,3,5)(2,4,5)(3,4,5)$の10通りあります。
この中で和が10以上になるのは$(1,4,5)(2,3,5)(2,4,5)(3,4,5)$の4通りあります。
よって、答えは$\frac{4}{10}=\frac{2}{5}$
問9 回答略
大問2 証明問題
Ｓさんのクラスでは、先生が示した問題をみんなで考えた。次の各問に答えよ。
問題文
［先生が示した問題］
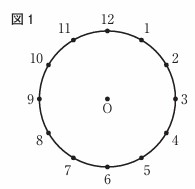
右の図1のように、円Ｏの円周を12等分する点に、1から12までの自然数の番号を、小さい順で時計回りに付ける。1から12までの番号を付けた点のうち、2点を結んでできる線分が円Ｏの直径となるとき、その2点を向かい合う点とする。
例えば、1の点と7の点は、向かい合う点である。
図1において、1組の向かい合う点を選び、それぞれの点の番号のうち、
小さい方の数をa、大きい方の数をbとする。
a，bの平均値をＡ，\(b^2-a^2\) の値をＢとするとき，ＢはＡの何倍か求めなさい。
問1
［先生が示した問題］で、ＢはＡの［ ］倍と表すとき、［ ］に当てはまる数を、次のア〜エのうちから選び、記号で答えよ。
ア 3 イ 4 ウ 6 エ 12
Ｓさんのグループは、［先生が示した問題］をもとにして、次の問題を作った。
［Ｓさんのグループが作った問題］
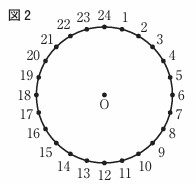
右の図2のように，円Ｏの円周を24等分する点に，
1から24までの自然数の番号を、小さい順で時計回りに付ける。
1から24までの番号を付けた点のうち、2点を結んでできる線分が円Ｏの直径となるとき，その2点を向かい合う点とする。
図2において，異なる2組の向かい合う点を選び、1組目のそれぞれの点の番号のうち，小さい方の数をa，大きい方の数をbとし，2組目のそれぞれの点の番号のうち，小さい方の数をc，大きい方の数をdとする。
a，b，c，dの平均値をＰ，bd-acの値をＱとするとき，Ｑ=24Ｐとなることを
確かめてみよう。
問2
［Ｓさんのグループが作った問題］で，Ｑ=24Ｐとなることを証明せよ。
解答・解説
問1 エ
問題文に与えられているように1と7を例にとって計算してみます。
$a=1,b=7$となるので、平均値Aは
$A=(1+7)\div2=4$となります。
次に、$B=b^2-a^2=7^2-1^2=48$となるので
BはAの12倍となります。
問2 下記参照
bをaを用いた式で表すと、
$b=a+12$
dをcを用いた式で表すと、
$d=c+12$
よって、
$P=\frac{a+b+c+d}{4}=\frac{a+c+12}{2}$
$24P=24\times\frac{a+c+12}{2}=12a+12c+144$…①
また、$Q=bd-ac=(a+12)(c+12)-ac=12a+12c+144$…②
①、②より$Q=24P$
0120-740-100
LINE問合せ窓口
LINEからもお問合せいただけます！
公式Instagram
勉強のお役立ち情報を配信中！
お問い合わせ、ご質問も受付中です！
ご質問などお気軽にお問い合わせください。
大問3 一次関数
問題文
右の図1で、点Oは原点、点Aの座標は(0, -4)であり、直線lは一次関数 \(\displaystyle y = \frac{1}{2}x + 3\) のグラフを表している。
直線lとx軸との交点をＢとする。直線l上にある点をＰとし，2点Ａ，Ｐを通る直線をmとする。
次の各問に答えよ。
問1
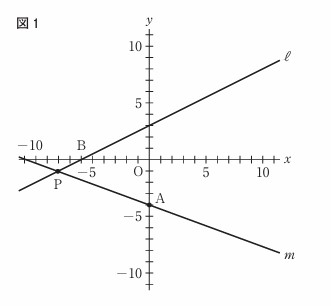
点Ｐのy座標が-1のとき、点Ｐのx座標を、次のア〜エのうちから選び、記号で答えよ。
ア -8 イ \(-\displaystyle\frac{9}{2}\) ウ -2 エ \(\displaystyle\frac{5}{2}\)
問2
点Pが点Bに一致するとき、直線mの式を、次のア～エのうちから選び、記号で答えよ。
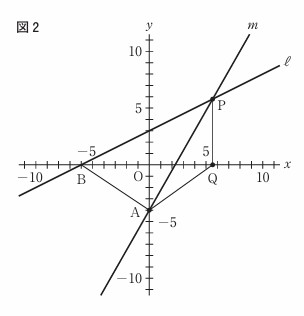
ア \(y = -\displaystyle\frac{3}{2}x – 4\)イ \(y = -\displaystyle\frac{3}{2}x – 6\)
ウ \(y = -\displaystyle\frac{2}{3}x – 4\)
エ \(y = -\displaystyle\frac{2}{3}x – 6\)
問3
右の図2は、図1において、点Ｐのx座標が正の数のとき、x軸上にありx座標が点Ｐのx座標と等しい点をＱとし、点Ａと点Ｂ、点Ａと点Ｑ、点Ｐと点Ｑをそれぞれ結んだ場合を表している。
△ＡＰＢの面積が△ＡＱＰの面積の2倍になるとき，点Ｐのx座標を求めよ。
解答・解説
問1 ア
点Pのｙ座標の値を直線lの式に当てはめれば求まります。
$-1=\frac{1}{2}x+3$
$x=-8$
問2 ウ
点Pが点Bに一致するときは、点Pのy座標は0となるので、問1と同様にして
$0=\frac{1}{2}x+3$
$x=-6$となり、点B(-6,0)だと分かります。
直線mは点Bと点Aの2点を通るので、それぞれ代入して連立方程式を解くと、直線の式が求まります。
点Aを代入して、$b=-4$…①
点Bを代入して$-6a+b=0$…②
①、②より、$a=-\frac{2}{3},b=-4$となるので、
直線mの式は$y=-\frac{2}{3}x-4$となります。
問3 7
点Pのx座標をsとすると、$点P(s,\frac{1}{2}s+3)$と表せます。
△APBの面積は$7\times(s+6)\div2$で求められ、
△AQPの面積は$s\times(\frac{1}{2}s+3)\div2$で求められます。
△APBが△AQPの面積の2倍となるので
$7s+42=2(\frac{1}{2}s^2+3s)$
$s^2-s-42=0$
$(s-7)(s+6)=0$
$s=7,-6$
$s>0$なので、$s=7$が答えとなります。
大問4 平面図形
問題文
右の図1で、点Oは線分ABを直径とする半円の中心である。点Pは、線分OA上にある点で、点O、点Aのいずれにも一致しない。
点Qは、弧AB上にある点で、点A、点Bのいずれにも一致しない。
点Rは、弧BQ上にある点で、点B、点Qのいずれにも一致しない。
点Aと点Q、点Aと点R、点Bと点Q、点Pと点Rをそれぞれ結ぶ。
次の各問に答えよ。
問1
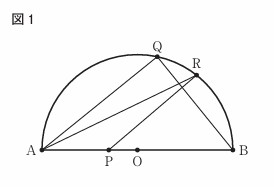
図1において、\(\stackrel{\frown}{AQ} = \stackrel{\frown}{BQ}\), \(\angle QAR = 20^\circ\), \(\angle ARP = a^\circ\) とするとき、\(\angle BPR\)の大きさを表す式を、次のア～エのうちから選び、記号で答えよ。
図1において、ＡＱ=ＢＱ、∠ＱＡＲ=20°、∠ＡＲＰ=a°とすると、∠ＢＰＲの大きさを表す式を、次のア〜エのうちから選び、記号で答えよ。
ア \((a+20)\)度 イ \((a+25)\)度 ウ \((155-a)\)度 エ \((160-a)\)度
問2
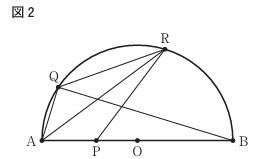
右の図2は、図1において、ＡＰ=ＡＱ，弧ＢＲ=弧ＱＲのとき、点Ｑと点Ｒを結んだ場合を表している。次の①、②に答えよ。
① △ＡＰＲ≡△ＡＱＲ であることを証明せよ。
② 次のの中の「う」「 え」に当てはまる数字をそれぞれ答えよ。図2において、線分ＡＲと線分ＢＱとの交点をＳ、点Ｏと点Ｒを結び、
線分ＢＱと線分ＯＲとの交点をＴとした場合を考える。ＡＰ=2ＯＰのとき，△ＲＳＴの面積は，四角形ＡＯＲＱの面積の
\(\displaystyle \frac{う}{え}\)倍である。
解答・解説
問1 イ
△AQBに注目すると直角二等辺三角形だと分かるので
∠QAB＝45°だと分かります。
よって、∠RAP＝45°－∠QAP＝25°
さらに△ARPに注目すると外角の性質から
∠BPR＝∠RAP+∠ARP＝$a+25$°が答えとなります。
問2 ①下記参照 ②【う】1【え】5
①
△APRと△AQRにおいて
共通な辺なので、$AR=AR$…①
仮定より、$AP=AQ$…②
仮定より、弧BR＝弧QR
等しい弧に対する円周角は等しいので
∠PAR＝∠QAR…③
①～➂より、2組の辺とその間の角がそれぞれ等しいので
△APR≡△AQR
②
AP：PO＝2：1からAQは2
△ABQ∽△OBTとり、OT＝1
半径は3なので、TR＝3-1＝2だと分かります。
錯覚とAQ＝RTより、△AQS≡△RTS
QS＝STからSはQTの中点だとわかります。
AQ//ORに注目すると
AQ+OR＝台形AORQ
△RSTは四角形AORQの$\frac{1}{5}$倍だと分かります。
LINE問合せ窓口
LINEからもお問合せいただけます！
公式Instagram
勉強のお役立ち情報を配信中！
お問い合わせ、ご質問も受付中です！
ご質問などお気軽にお問い合わせください。
大問5 空間図形
問題文
右の図1に示した立体ＡＢＣＤ-ＥＦＧＨは、ＡＢ=ＡＤ=6cm、ＡＥ=4cmの直方体である。
頂点Ａと頂点Ｃを結び、線分ＡＣ上にある点をＰとする。
頂点Ｈと点Ｐを結ぶ。
次の各問に答えよ。
問1
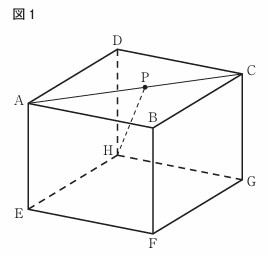
次の[ ]の中の「お」「 か」に当てはまる数字をそれぞれ答えよ。図1において、頂点Ｄと点Ｐ、頂点Ｅと点Ｐをそれぞれ結んだ場合を考える。
点Ｐが線分ＡＣの中点のとき、立体Ｐ-ＡＥＨＤの体積は、 [ おか ]cm3 である。
問2
次の[ ]の中の「き」「 く」「 け」に当てはまる数字をそれぞれ答えよ。
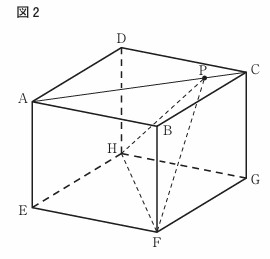
右の図2は、図1において、頂点Ｆと頂点Ｈ、頂点Ｆと点Ｐをそれぞれ結んだ場合を表している。
ＡＰ：ＰＣ=5：1のとき、△ＦＰＨの面積は
[きく]\(\sqrt{[け]}\) cm\(^2\)
解答・解説
問1 【お】2 【か】4
底面が四角形AEHDの立体になります。
点PからADに垂線を下した交点を点Qとすると、高さはPQで表せます。
△APDは直角二等辺三角形になるので、PQ＝3cm
よって、$4\times6\times3\div3=24cm^3$となります。
問2 【き】1 【く】２ 【け】3
△EFHは直角二等辺三角形になるので、△EPHの底辺となるFHは$6\sqrt{2}cm$となります。
また、点Pから降ろした垂線の交点をOとします。
△PFHも直角二等辺三角形であることに気づくと、POの長さが三平方の定理から求まりそうなことに気が付きます。
そのために、ORの長さを求めます。
EGを結び、PからEGへの垂線をRとすると
OR＝EG－（EO+RG）で求まります。
EGは3、RG＝PC＝1となるので、ORの比は2となります。
$EG:OR＝6:2＝6\sqrt{2}:OR$
$OR=2\sqrt{2}cm$
よって、△FPHの面積は$6\sqrt{2}\times2\sqrt{6}\div2=12\sqrt{3}cm^2$となります。
志望校に合わせた受験対策なら、やる気アシストにお任せ下さい！
家庭教師のやる気アシストは、東京都にお住まいの受験生のお子さんを毎年たくさん指導をさせ頂き、合格に導いています。
高い合格率の秘訣は、指導経験豊富な先生の指導力に加え、1対1の指導でお子さん一人ひとりの状況に合わせた、お子さんだけのカリキュラムで勉強が進められるから！
家庭教師のやる気アシストは、お子さんの志望校合格まで全力でサポートさせて頂きます！
LINE問合せ窓口
LINEからもお問合せいただけます！
公式Instagram
勉強のお役立ち情報を配信中！
お問い合わせ、ご質問も受付中です！
ご質問などお気軽にお問い合わせください。
アシストの指導方法がじっくり見れる！知れる！無料の体験授業実施中
お子さんにとって「成果が出る勉強法」ってどんな勉強法だと思いますか？
お子さんそれぞれに、個性や性格、学力の差もあります。そんな十人十色のお子さん全員に合う勉強法ってなかなかないんです。
たからこそ、受験生の今だけでもお子さんだけの勉強法で受験を乗り越えてみませんか？
やる気アシストには、決まったカリキュラムはありません。お子さんの希望や学力、得意や不得意に合わせて、お子さんだけのカリキュラムで指導を行っていきます。また、勉強法もお子さんそれぞれに合う合わないがあります。無料体験授業では、お子さんの性格や生活スタイルを見せていただき、お子さんにとって効率的な成果の出る勉強のやり方をご提案させて頂きます。
