






和歌山県の2022年3月実施の令和4年度(2022年度)入学者の公立高校入試問題の解説をしています。
受験勉強において、過去問を解くことはとても効果的な勉強法です。ぜひ、受験までに一度挑戦し、問題の傾向を掴んでおきましょう。合わせて、対策などをたてられるととても良いですね。
また、過去問で苦手な点が見つかった場合は、そこを中心に試験日当日までにしっかりと対策しておきましょう。
今年の和歌山県の数学は5つの大問で構成され、小問集合が2つ、法則性を問う問題(数列)、関数、図形となっています。
難易度としては例年よりも難しくやや難です。ただ設問毎のつながりが薄いので、解ける問題を落とさずに得点していくことが大事になってくるように思います。
次の[問1]~[問6]に答えなさい。
[問1]次の(1)~(5)を計算しなさい。
(1)-9+4
(2)10/3+2÷(-3/4)
(3)(3a+5b)+2(2a-b)
(4)√48-√3+√12
(5)(a+3)²-(a+4)(a-4)
[問2]次の二次方程式を解きなさい。
x²+5x-14=0
[問3]√20/nの値が自然数となるような自然数nを、全て求めなさい。
[問4]yはxに反比例し、x=5のとき、y=4である。
x=-10のとき、yの値を求めなさい。
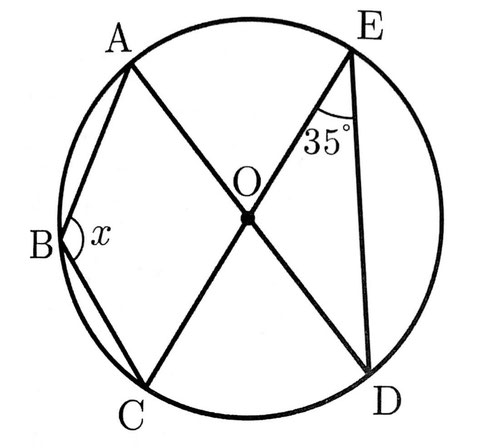
[問5]右の図のように、円Oの周上に、5点A,B,C,D,Eがあり、線分AD,CEはともに円Oの中心を通る。
∠CED=35°のとき、∠xの大きさを求めなさい。
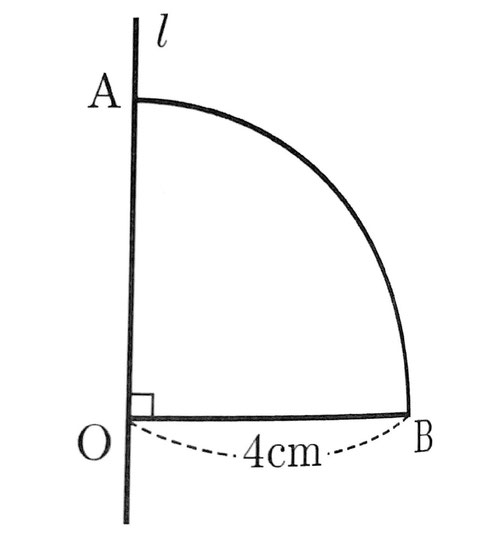
[問6]右の図のおうぎ形OABは、半径4cm、中心角90°である。
このおうぎ形OABを、AOを通る直線lを軸として1回転させてできる立体の体積を求めなさい。ただし、円周率はπとする。
【解答】
[問1]
(1)-5 (2)2/3 (3)7a+3b (4)5√3 (5)6a+25
[問2]
x=-7,2
[問3]
n=5,20
[問4]
y=-2
[問5]
∠x=125(度)
[問6]
128π/3(cm³)
【解説】
[問1]
(2)10/3+2×(-4/3)=10/3-8/3=2/3
(3)3a+5b+4a-2b=7a+3b
(4)4√3-√3+2√3=5√3
(5)(a²+6a+9)-(a²-16)=6a+25
[問2]
(x+7)(x-2)=0 x=-7,2
[問3]
√2²×5/nより、n=5のとき√2²×5/5=2 n=20のとき√2²×5/20=1
[問4]
y=a/xとおき、x=5,y=4を代入すると、4=a/5 a=20
y=20/xに、x=-10を代入すると、y=20/-10=-2
[問5]
△ODEは、OE=ODの二等辺三角形だから、
∠ODE=∠OED=35°、∠EOD=180°-35°×2=110°
△ODEで、三角形の外角の性質より、
∠AOE=∠COD=35°+35°=70°
∠xは、弧AECの円周角だから、円周角の定理より、
∠x=1/2(∠AOE+∠EOD+∠COD)
=1/2(70°+110°+70°)=125°
[問6]
半径4cmの半球になるから、求める体積は、
1/2×(4π/3×4³)=128π/3(cm³)
次の[問1]~[問4]に答えなさい。
[問1]Aさん、Bさん、Cさん、Dさんの4人がリレーで走る順番を、次の方法で決める。
[問2]図のように、5色のリングを左から青、黄、黒、緑、赤の順に繰り返し並べていく。下の表は、並べたときのリングの順番と色についてまとめたものである。
このとき、下の(1)、(2)に答えなさい。
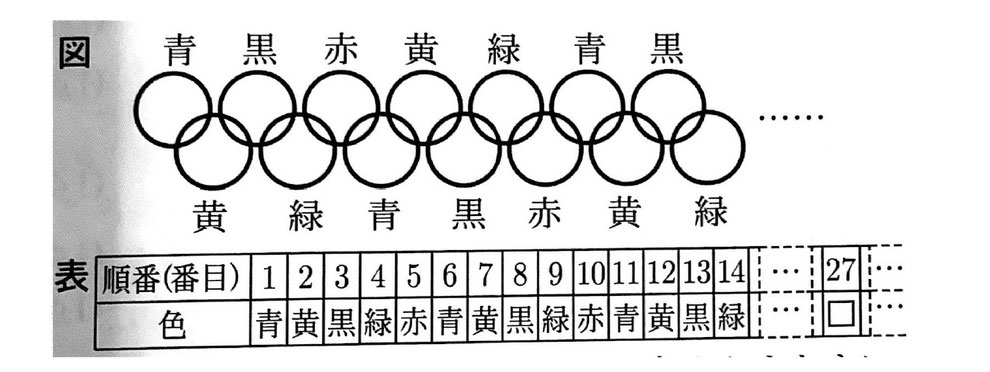
(1)表中の□にあてはまる27番目の」色を書きなさい。
(2)124番目までに、黒色のリングは何個あるか、求めなさい。
[問3]あるスーパーマーケットでは、から揚げ弁当とエビフライ弁当を、それぞれ20個ずつ販売している。エビフライ弁当1個の定価は、から揚げ弁当1個の定価より50円高い。エビフライ弁当は、すべて売り切れたが、から揚げ弁当が売れ残りそうだったので、から揚げ弁当10個を定価の5割引きにしたところ、2種類の弁当をすべて売り切ることができた。その結果、2種類の弁当の売り上げの合計は、1500円となった。
このとき、から揚げ弁当1個とエビフライ弁当1個の定価はいくらか、求めなさい。ただし、答えを求める過程がわかるようにかきなさい。なお、消費税は考えないものとする。
[問4]和夫さんと紀子さんの通う中学校の3年生の生徒数は、A組35人、B組35人、C組34人である。図書委員の和夫さんと紀子さんは、3年生のすべての生徒について、図書室で1学期に借りた本の冊数の記録を取り、その記録をヒストグラムや箱ひげ図に表すことにした。次の図は、3年生の生徒が1学期に借りた本の冊数の記録を、クラスごとに箱ひげ図に表したものである。
次の(1)~(3)に答えなさい。
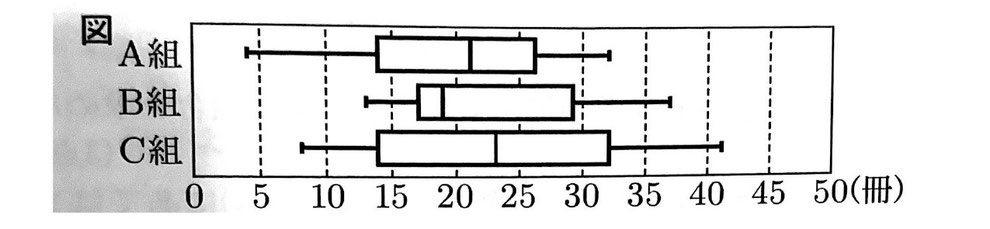
(1)和夫さんは、図から読み取れることとして、次のように考えた。
【和夫さんの考え】
(Ⅰ)四分位範囲が最も大きいのはA組である。
(Ⅱ)借りた本の冊数が20冊以下である人数が最も多いのはB組である。
(Ⅲ)どの組にも、借りた本の冊数が30冊以上の35冊以下の生徒が必ずいる。
図から読み取れることとして、和夫さんの考え(Ⅰ)~(Ⅲ)はそれぞれ正しいといえますか。次のア~ウの中から最も適切なものを1つずつ選び、その記号を書きなさい。
ア 正しい イ 正しくない ウ この資料からはわからない
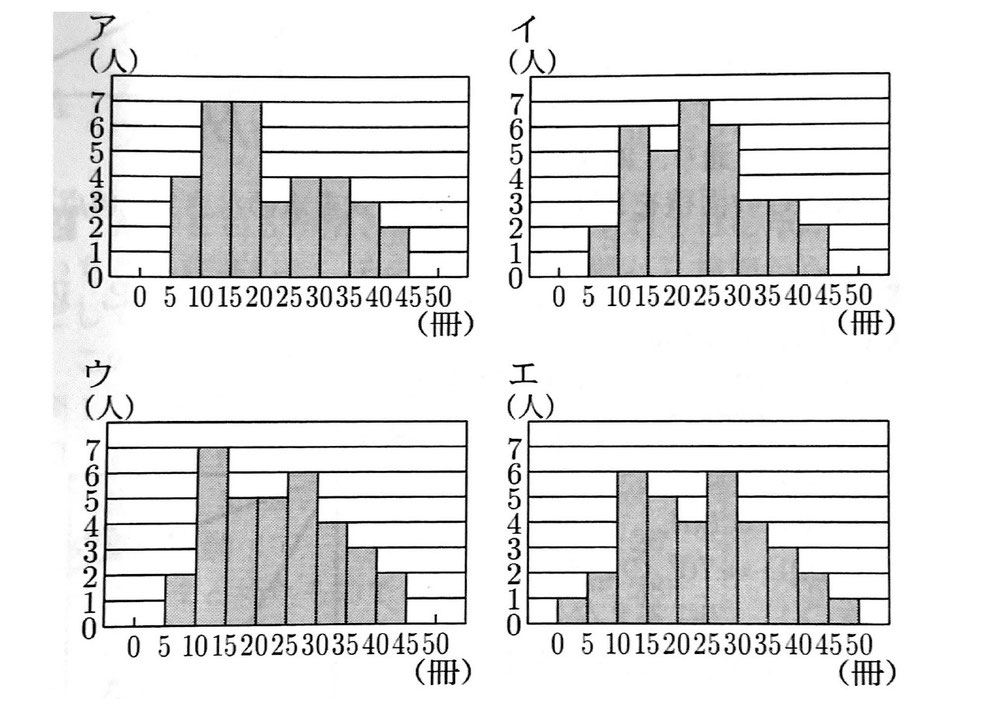
(2)C組の記録をヒストグラムに表したものとして最も適切なものを、次のア~エの中から1つ選び、その記号を書きなさい。
(3)和夫さんと紀子さんは、「この中学校の生徒は、どんな本が好きか」ということを調べるために、アンケート調査をすることにした。次の文は、調査についての2人の会話の一部である。
紀子:1年生から3年生までの全校生徒300人にアンケート調査をするのは人数が多くてたいへんだから、標本調査をしましょう。
和夫:3年生の生徒だけにアンケート調査をして、その結果をまとめよう。
紀子:その標本の取り出し方は適切ではないよ。
下線部について、紀子さんが適切ではないといった理由を、簡潔に書きなさい。
【解答】
[問1]
1/12
[問2]
(1)黄(色) (2)25(個)
[問3]
(例)から揚げ弁当1個の定価をx円、エビフライ弁当1個の定価をy円とすると、
y=x+50
10x+0.5x×10+20y=150000
これを解いて、x=400,y=450
よって、から揚げ弁当1個の定価400円 エビフライ弁当1個の定価450円
[問4]
(1)(Ⅰ)イ (Ⅱ)ア (Ⅲ)ウ
(2)ウ
(3)(例)標本を無作為に抽出したことにならないため。
【解説】
[問1]
リレーの走る順番は全部で、4×3×2×1=24(通り)
第一走者がAさん、第四走者がDさんとなる場合は、走る順に、Aさん、Bさん、Cさん、Dさん、または、Aさん、Cさん、Bさん、Dさんの2通り。
よって、求める確率は、2/24=1/12
[問2]
(1)5色を使っているので、5番目、10番目、15番目、…のように5で割り切れる順番は赤色になる。よって、25番目が赤色、26番目が青色、27番目が黄色になる。
(2)5×24=120より、120番目までに、黒色は24個ある。123番目が黒色だから、24+1=25(個)
[問4]
(1)
(Ⅰ)四分位範囲は箱の横の長さにあたるから、四分位範囲が最も大きいのはC組である。
(Ⅱ)B組の中央値は20冊未満の値、A,C組の中央値は20冊より大きい値なので、正しい。
(Ⅲ)B組の箱ひげ図を見ると、30冊以上35冊以下はひげの一部なので、30冊以上35冊以下の生徒がいるかどうか判断できない。
(2)C組の箱ひげ図から、最小値は5冊より大きく、10冊未満の値で、最大値は40冊より大きく45冊未満の値であるから、エは誤り。また、C組は34人だから、第1四分位数は少ない方から9番目の冊数で、箱ひげ図から、10冊より大きく15冊未満の値になる。イは、ヒストグラムより、15冊未満の人数が2+6=8(人)となり、少ない方から9番目の冊数は15人以上だから誤り。さらに、C組は34人だから、中央値は少ない方から17番目と18番目の冊数の平均値で、箱ひげ図から、20冊より大きく25冊未満の値になる。アは、ヒストグラムより、20冊未満の人数が4+7+7=18(人)となり、少ない方から17番目と18番目の冊数の平均値は20冊未満だから誤り。ウは、C組の箱ひげ図の第1四分位数、中央値、第3四分位数を満たしている。
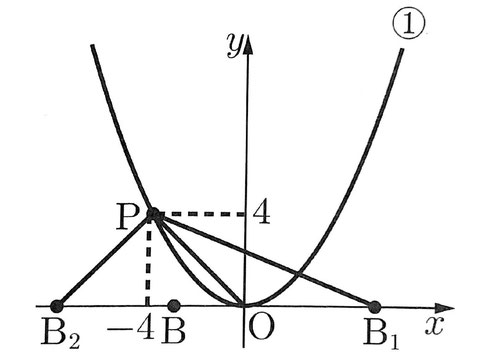
図1のように、関数y=1/4x²…①のグラフ上に点A(-2,1)がある。また、点Pは、①のグラフ上の点である。
次の[問1]~[問4]に答えなさい。
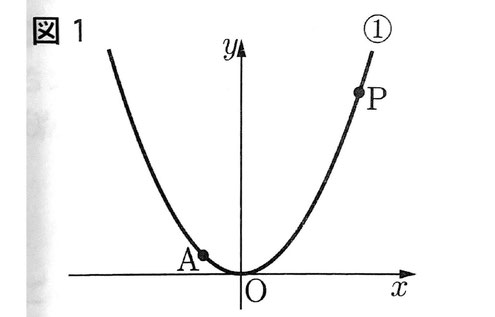
[問1]関数y=1/4x²について、xの値が-2から0まで増加するときの変化の割合を求めなさい。
[問2]次の文中の(ア)、(イ)にあてはまる数を求めなさい。
関数y=1/4x²について、xの変域が-2≦x≦(ア)のとき、yの変域は(イ)≦y≦9である。
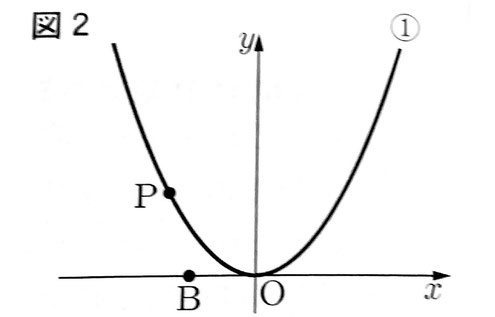
[問3]図2のように、x軸上に点Bをとる。Pのx座標が-4のとき、△OPBが二等辺三角形となるようなBはいくつかある。
そのうち、x座標が最も大きいBの座標と、x座標が最も小さいBの座標を、それぞれ求めなさい。
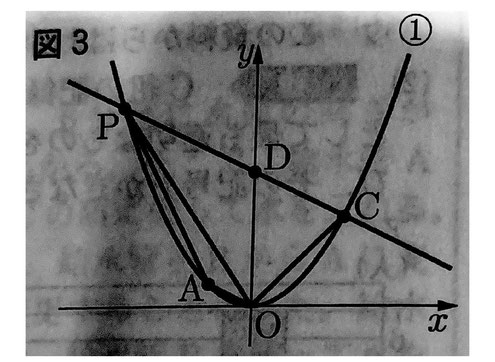
[問4]図3のように、①のグラフ上に点C(4,4)があり、直線PCとy軸との交点をDとする。
△OPDと△ODCの面積比が3:2であるとき、Aを通り、四角形OAPCの面積を2等分する直線の式を求めなさい。
【解答】
[問1]-1/2
[問2](ア)6 (イ)0
[問3]x座標が最も大きい座標:B(4√2,0) x座標が最も小さい座標:B(-8,0)
[問4]y=5/2x+6
【解説】
[問1]x=-2のときy=1 x=0のときy=0より、変化の割合は、(0-1)/(0-(-2))=-1/2
[問2]x=-2のときy=1で、yの最大値は9だから、y=1/4x²にy=9を代入して、9=1/4x² x=±6 -2≦xより、x=6…(ア)
また、xの変域が-2≦x≦6のとき、yの最小値は0…(イ)
[問3]P(-4,4)
x座標が最も大きいBの位置をB₁、x座標が最も小さいBの位置をB₂とすると、右図のようになる。
OP=OB₁=4√2より
B₁(4√2,0)
また、OP=OB₂より
OB₂=8だから、B₂(-8,0)
[問4]△OPDと△ODCは、辺ODを底辺とみると、高さの比が3:2となる。
よって、△OPDの高さは、4×3/2=6
すなわち、Pのx座標は-6となるから、P(-6,9)
直線PCは、y=-1/2x+6となるので、D(0,6)
これまでのことから、四角形OAPCは、OA//CPの台形となる。三平方の定理より、
OA=√1²+2²=√5
CP=√5²+10²=5√5
OA:CP=1:5だから、点Aを通り、四角形OAPCの面積を2等分する直線と、辺CPとの交点をQとすると、CQ:QP=2:3となればよい。図3から、点Qと点Dは一致する。
したがって、求める直線は、点Aと点Dを通る直線である。
傾きは(6-1)/(0-(-2))=5/2より、y=5/2x+6
1辺が6cmの正方形ABCDの辺BC上に点P、辺CD上に点Qがある。
次の[問1]~ [問3]に答えなさい。
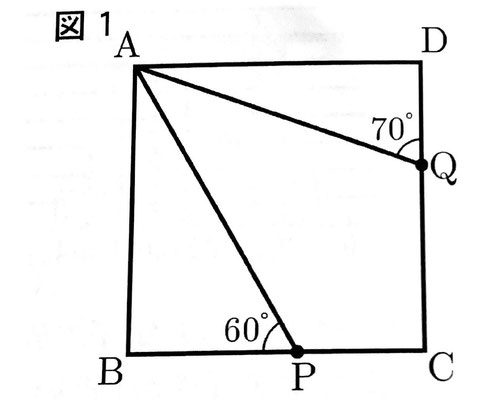
[問1]図1のように、∠APB=60°、∠AQD=70°のとき、次の(1)、(2)に答えなさい。
(1)∠PAQの大きさを求めなさい。
(2)△ABPの面積を求めなさい。
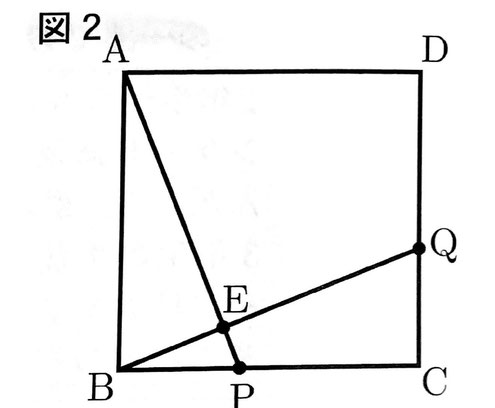
[問2]図2のように、BP=CQのとき、BQとAPとの交点をとする。
このとき、∠AEB=90°であることを証明しなさい。
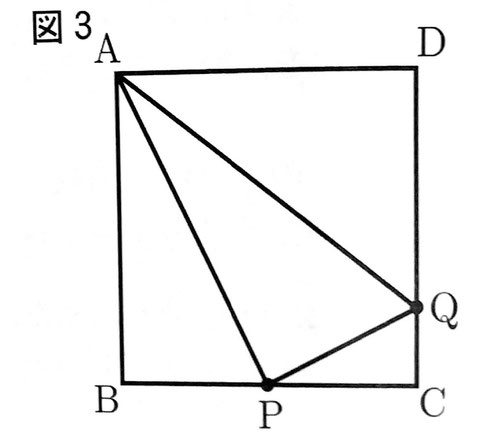
[問3]図3のように、BP=PC、∠BAP=∠CPQとする。
このとき、3点A,P,Qを通る円の半径を求めなさい。
【解答】
[問1](1)∠PAQ=40(度) (2)6√3(cm²)
[問2](例)△ABPと△BCQで、
過程より、BP=CQ…①
AB=BC…②
∠ABP=∠BCQ…③
①、②、③から、2組の辺とその間の角がそれぞれ等しいので、
△ABP≡△BCQ
対応する角野大きさは等しいから、
∠APB=∠BQC…④
また、△BCQは∠BCQ=90°の直角三角形であるから、
∠BQC+∠CBQ=90°…⑤
④、⑤より、
∠APB+∠CBQ=90°…⑥
△BPEで、三角形の外角の性質より、
∠EPB+∠PBE=∠AEB…⑦
⑥、⑦より、∠AEB=90°
[問3]15/4(cm)
【解説】
[問1]
(1)△ABPで、
∠BAP=180°-(90°+60°)=30°
△AQDで、∠QAD=180°-(90°+70°)=20°
∠PAQ=∠BAD-(∠BAP+∠QAD)
=90°-(30°+20°)
=40°
(2)△ABPは∠BPA=60°の直角三角形だから、
BP=1/√3AB=2√3(cm)
したがって、△ABP=1/2×2√3×6=6√3(cm²)
[問3]△ABPと△PCQにおいて、
仮定より、∠BAP=∠CPQ…①
∠ABP=∠PCQ…②
①、②から、2組の角がそれぞれ等しいので、
△ABP∽△PCQ
対応する角野大きさは等しいので、∠APB=∠PQC…③
また、△PCQは、∠PCQ=90°の直角三角形だから、
∠PQC+∠CPQ=90°…④
③、④より、∠APB+∠CPQ=90°となり、
∠APQ=180°-(∠APB+∠CPQ)=90°
よって、円周角の定理より、3点A,P,Qを通る円の直径は線分AQとなる。
△ABP∽△PCQより、AB:PC=BP:CQ
6:3=3:CQ
CQ=3/2(cm)
よって、DQ=DC-CQ=6-3/2=9/2(cm)
△AQDで、三平方の定理より、
AQ=√6²+(9/2)²=15/2(cm)
したがって、求める円の半径は、15/2×1/2=15/4(cm)
家庭教師のやる気アシストは、過去の入試問題も分析し和歌山県の入試問題の傾向やチェックポイントなどをまとめて、受験対策を行っています。
家庭教師のやる気アシストは高校受験に強い家庭教師!昨年度の合格率は、関西エリア全体で97.3%という結果を残すことが出来ました!その 高い合格率の秘訣は、過去問を分析した対策や指導経験豊富な先生の指導力に加え、1対1の指導でお子さん一人ひとりの状況に合わせた、お子さんだけのカリキュラムで勉強が進められるから!
家庭教師のやる気アシストなら、お子さんの志望校に合わせた指導で合格まで全力でサポートさせて頂きます!
受験当日までの限られた時間です。少しでも気になった方は、すぐにお問合せ下さい!
1日でも早く対策を始めることが合格への近道です。
お子さんにとって「成果が出る勉強法」ってどんな勉強法だと思いますか?
お子さんそれぞれに、個性や性格、学力の差もあります。そんな十人十色のお子さん全員に合う勉強法ってなかなかないんです。
たからこそ、受験生の今だけでもお子さんだけの勉強法で受験を乗り越えてみませんか?
やる気アシストには、決まったカリキュラムはありません。お子さんの希望や学力、得意や不得意に合わせて、お子さんだけのカリキュラムで指導を行っていきます。また、勉強法もお子さんそれぞれに合う合わないがあります。無料体験授業では、お子さんの性格や生活スタイルを見せていただき、お子さんにとって効率的な成果の出る勉強のやり方をご提案させて頂きます。

