







栃木県の2023年3月実施の令和5年度(2023年度)入学者の公立高校入試問題の解説をしています。
受験勉強において、過去問を解くことはとても効果的な勉強法です。ぜひ、受験までに一度挑戦し、問題の傾向を掴んでおきましょう。合わせて、対策などをたてられるととても良いですね。
また、過去問で苦手な点が見つかった場合は、そこを中心に試験日当日までにしっかりと対策しておきましょう。
次の1から8までの問いに答えなさい。
(1)$3-(-5)$を計算しなさい。
(2)$8a^3b^2 \div 6ab$を計算しなさい。
(3)$(x+3)^2$を展開しなさい。
(4)1個x円のパンを7個と1本y円のジュースを5本買ったところ、代金の合計が2000円以下になった。この数量の関係を不等式で表しなさい。
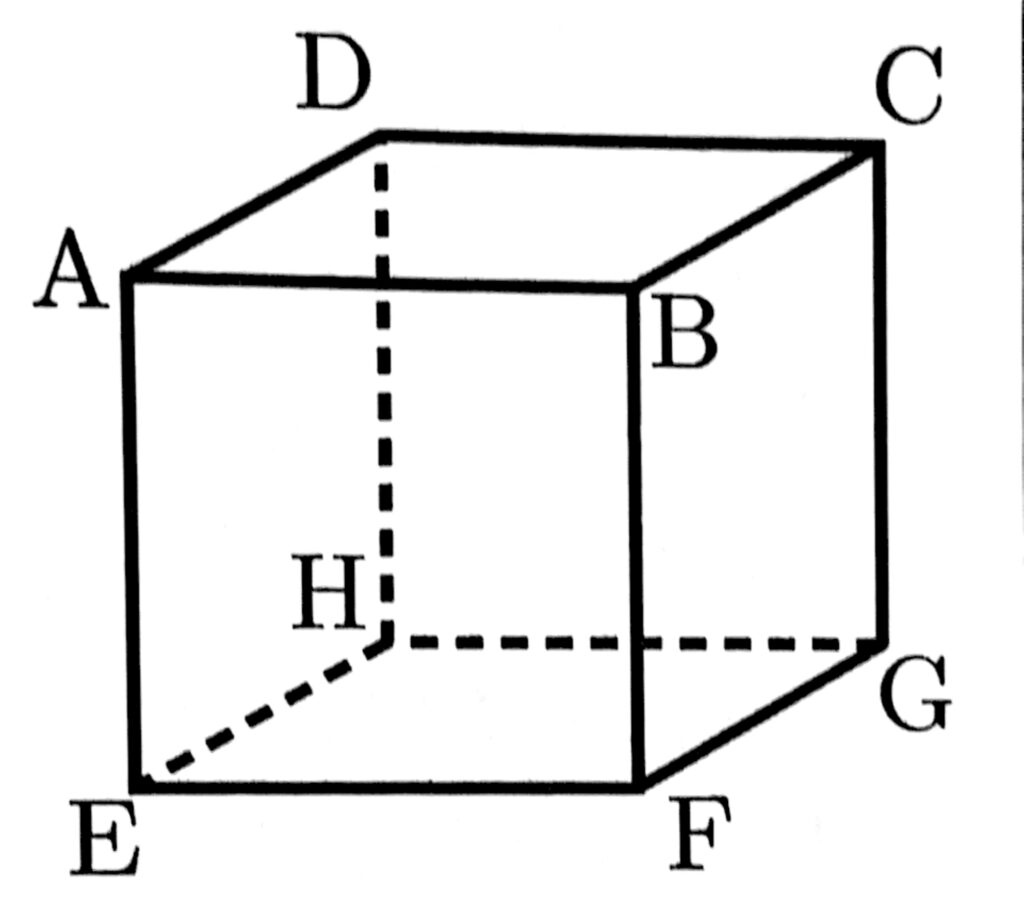
(5)次の図の立方体ABCD-EFGHにおいて、辺ABとねじれの位置にある辺の数はいくつか。
(6)yはxに反比例し、x=-2のとき、y=8である。yをxの式で表しなさい。
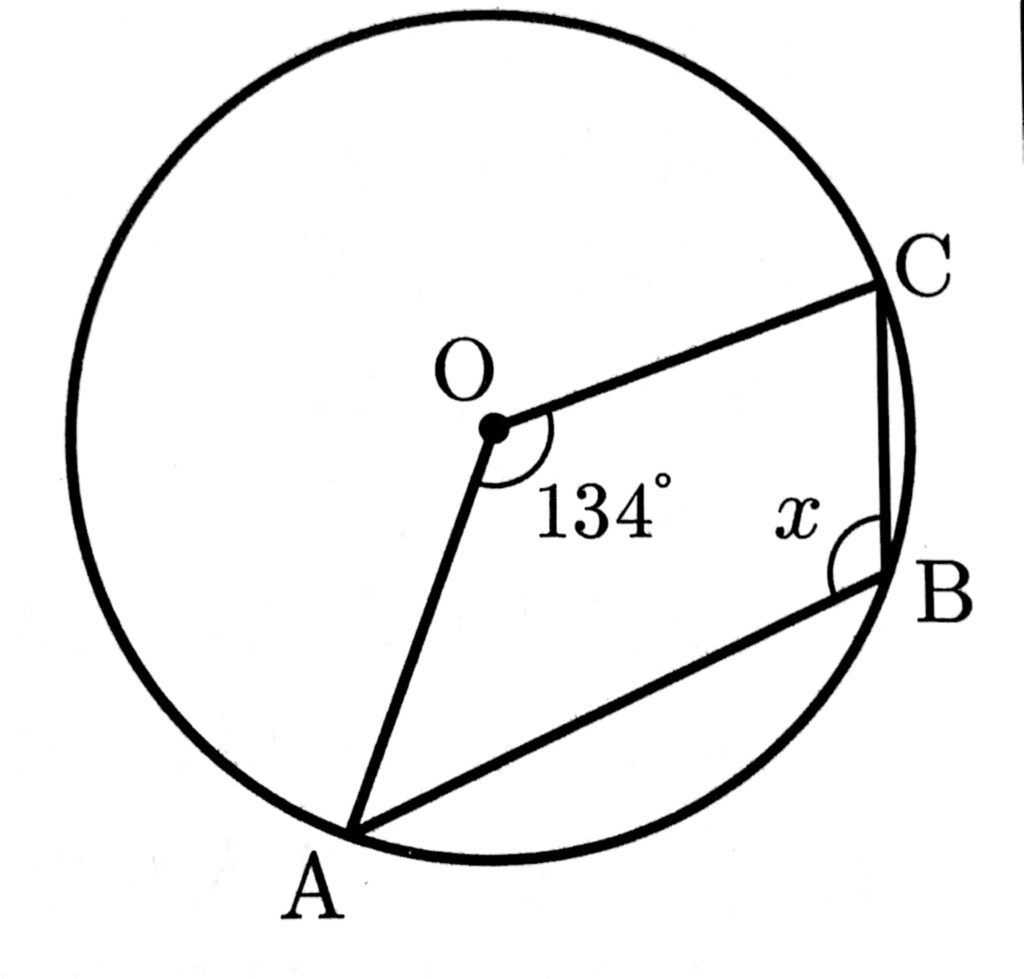
(7)次の図において、点A、B、Cは円Oの周上の点である。∠xの大きさを求めなさい。
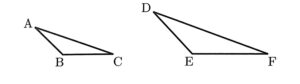
(8)△ABCと△DEFは相似であり、その相似比は3:5である。このとき、△DEFの面積は△ABCの面積の何倍か求めなさい。
(1)$3-(-5)= 3 + 5 = 8$
(2)$\frac{8a^3b^2}{6ab} = \frac{4a^2b}{3}$
(3)$(x + 3)^2 = x^2 + 6x + 9$
(4)$7x + 5y \le 2000$
(5)辺ABとねじれの位置にある辺は、辺EH、辺FG、辺DH、辺CGの4つ
(6)$y$は$x$に反比例するので、$y = \frac{a}{x}$($a$は定数)とおく。 $x = -2$、$y = 8$を上式に代入すると、$8 = \frac{a}{-2}$
これを解くと、$a = -16$ よって、$y = -\frac{16}{x}$
(7)点Bを含まない弧AC上の点をDとする。 円周角の定理より、$\angle\text{ADC} = \frac{1}{2}\angle\text{AOC} = \frac{1}{2} \times 134^\circ = 67^\circ$ $\angle x = 180^\circ – \angle\text{ADC} = 180^\circ – 67^\circ = 113^\circ$
(8)$\triangle\text{ABC}$と$\triangle\text{DEF}$の相似比は$3:5$であり、面積比は相似比の2乗と等しいので、$\triangle\text{ABC}$と$\triangle\text{DEF}$の面積比は$9:25$
よって、$\triangle\text{DEF}$の面積は$\triangle\text{ABC}$の面積の$\frac{25}{9}$倍
次の1,2,3の問いに答えなさい。
(1)2次方程式$x^2+4x+1=0$を解きなさい。
(2)ある高校では、中学生を対象に一日体験学習を各教室で実施することにした。使用できる教室の数と参加者の人数は決まっている。1つの教室に入る参加者を15人ずつにすると、34人が教室に入れない。また、1つの教室に入る参加者を20人ずつにすると、14人の教室が1つだけでき、さらに使用しない教室が1つできる。
このとき、使用できる教室の数をxとして方程式をつくり、使用できる教室の数を求めなさい。ただし、途中の計算も書くこと。
(3)次の先生と生徒の会話文を読んで、生徒が完成させた【証明】の①~⑤に当てはまる数や式をそれぞれ答えなさい。
先生 「一の位が0でない 900未満の3けたの自然数をMとし, M に 99 をたしてできる自然数をNとすると,M の各位の数の和とNの各位の数の和は同じ値になるという性質があります。 例として583 で確かめてみましょう。」
生徒 「583の各位の数の和は5+8+3= 16 です。583 に 99 をたすと 682 となるので,各位の数の和は 6+8+2=16で同じ値になりました。」
先生 「そうですね。 それでは,M の百の位, 十の位,一の位の数をそれぞれ a, b, cとして,この性質を証明してみましょう。 a, b, c のとりうる値の範囲に気をつけて, MとNをそれぞれ a,b c を用いて表すとどうなりますか。」
生徒 「Mは表せそうですが, N は M + 99 で…,各位の数がうまく表せません。」
先生 「99を100-1 におきかえて考えてみましょう。」
生徒が完成させた【証明】
3けたの自然数Mの百の位、十の位、一の位の数をそれぞれa,b,cとすると、aは1以上8以下の整数、bは0以上9以下の整数、cは1以上9以下の整数となる。
このとき、
M=①×a+②×b+cと表せる。
また、N=M+99より
N=①×a+②×b+c+100-1
となるから
N=①×(③)+②×④+⑤
となり、
Nの百の位の数は③、十の位の数は④、一の位の数は⑤となる。
よって、Mの各位の数の和とNの各位の数の和はそれぞれa+b+cとなり、同じ値になる。
(1)$x = -2 \pm\sqrt{3}$
解の公式より、
$x = \frac{-4\pm\sqrt{4^2-4\times1\times1}}{2\times1} = \frac{-4\pm\sqrt{12}}{2} = \frac{-4\pm2\sqrt{3}}{2} = -2\pm\sqrt{3}$
(別解)
$x^2 + 4x + 4 = 3$
$(x + 2)^2 = 3$
$x + 2 = \pm\sqrt{3}$
$x = -2 \pm\sqrt{3}$
(2)使用できる教室の数は12
「1つの教室に入る参加者を15人ずつにすると、34人が教室に入れない。」より、参加者の人数を$x$の式で表すと、
$15x + 34(\text{人})$
「1つの教室に入り参加者を20人ずつにすると14人の教室が1つだけでき、さらに使用しない教室が1つできる。」より、参加者の人数を$x$の式で表すと、
$20(x-2) + 14 = 20x – 40 + 14 = 20x – 26(\text{人})$
以上より、
$15x + 34 = 20x – 26$
$15x + 34 = 20(x – 2) + 14$
$15x + 34 = 20x – 26$
$-5x = -60$
$x = 12$
この解は問題に適している。
よって、使用できる教室の数は12となる。
(3)①100 ②10 ③$a+1$ ④$b$ ⑤$c-1$
③④⑤は、1つ前の式を 100、10、1それぞれについて共通因子を持つ項ごとに因数分解して考える。
次の1,2,3の問いに答えなさい。
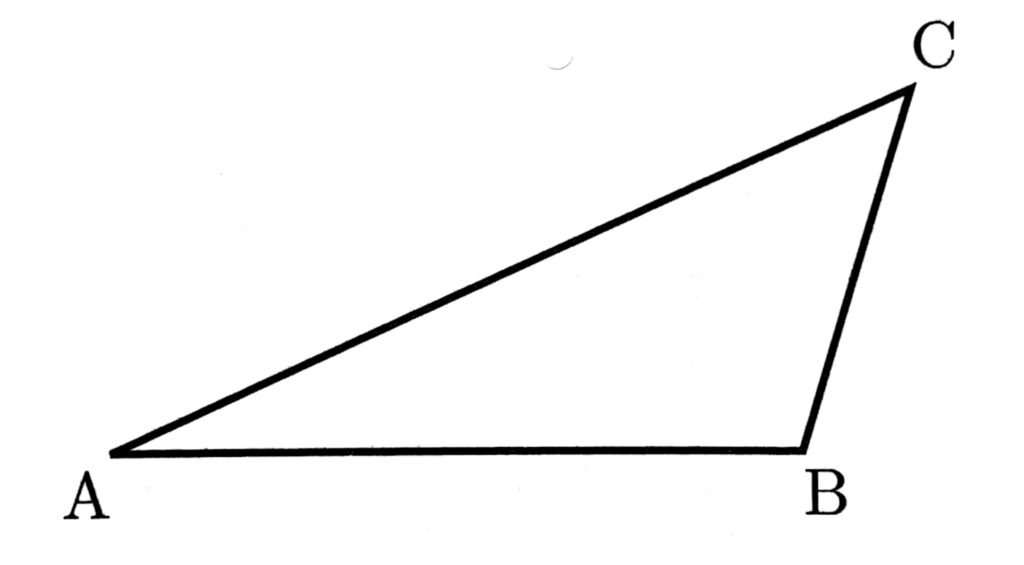
(1)次の図の△ABCにおいて、辺AC上にあり、∠ABP=30°となる点Pを作図によって求めなさい。ただし、作図には定規とコンパスを使い、また、作図に用いた線は消さないこと。
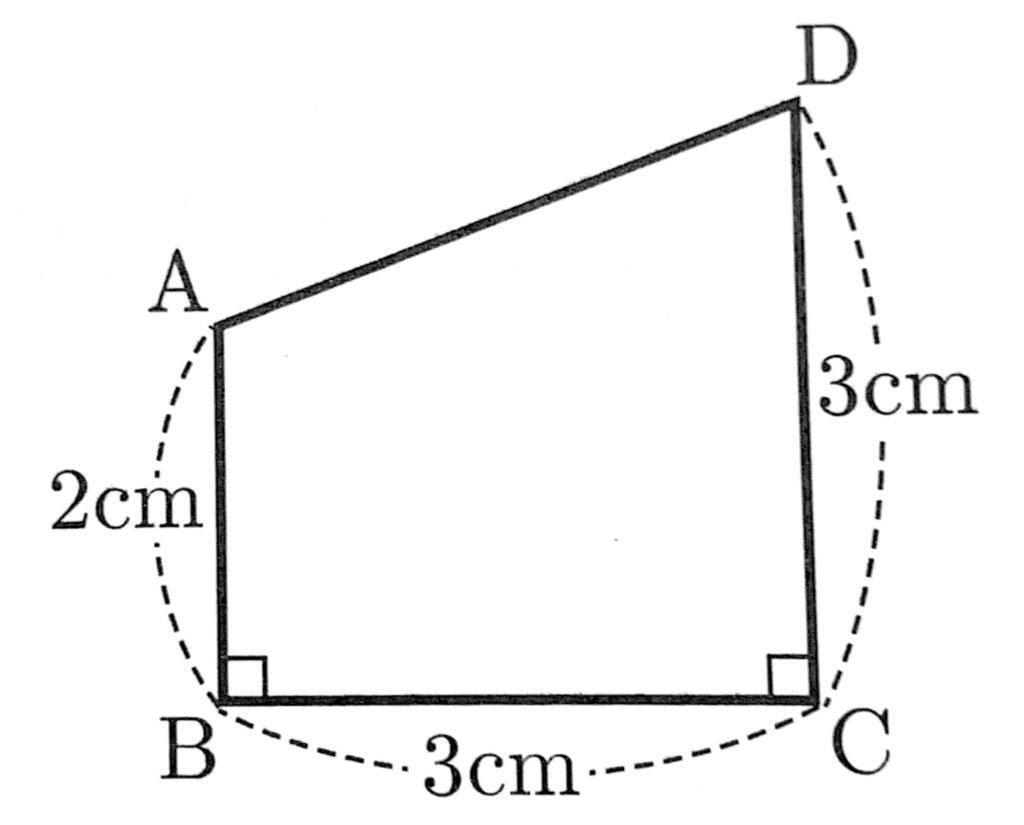
(2)次の図は、AB=2cm、BC=3cm、CD=3cm、∠ABC=∠BCD=90°の台形ABCDである。このとき、次の(1)(2)の問いに答えなさい。
① ADの長さを求めなさい。
② 台形ABCDを、辺CDを軸として1回転させてできる立体の体積を求めなさい。ただし、円周率はπとする。
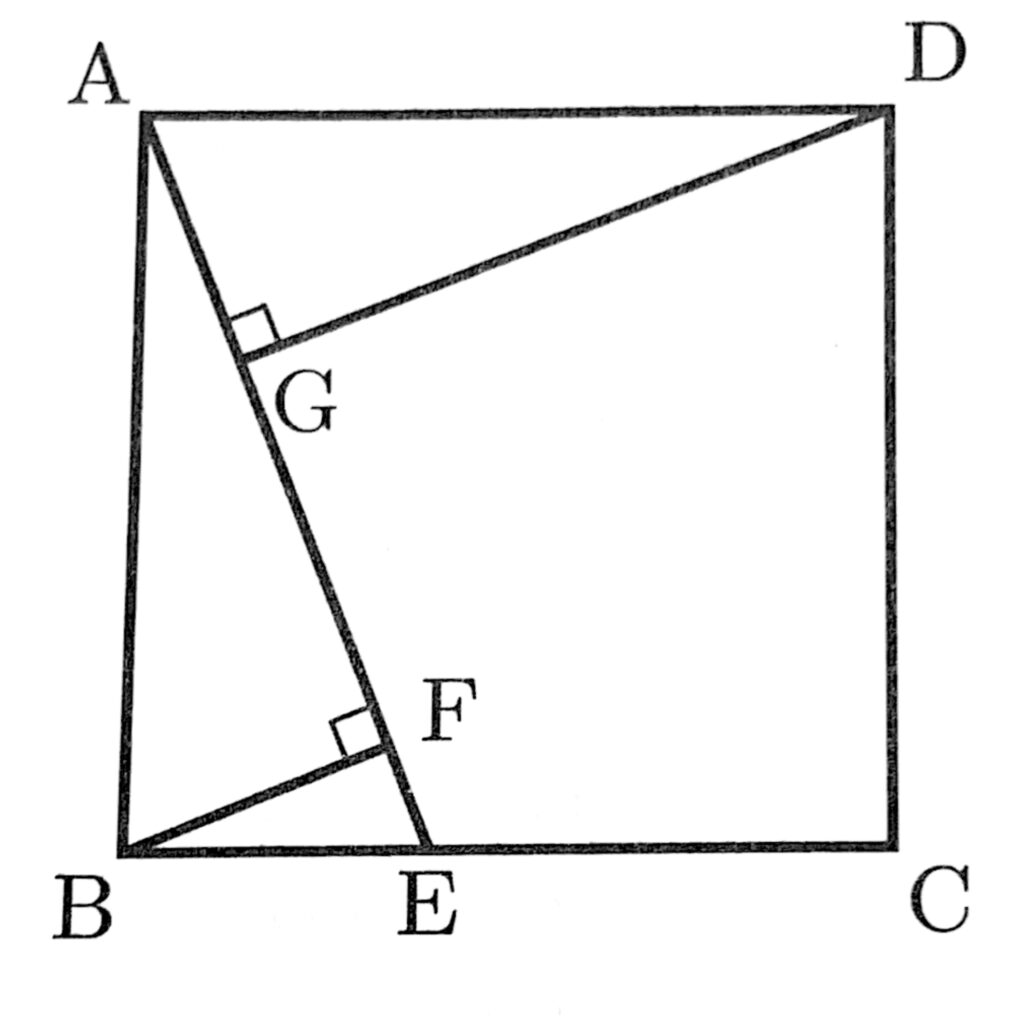
(3)次の図のように、正方形ABCDの辺BC上に点Eをとり、頂点B,Dから線分AEにそれぞれ垂線BF,DGをひく。
このとき、△ABF≡△DAGであることを証明しなさい。
正三角形の1つの角の大きさは$60^\circ$であることを利用する。辺ABを一つの辺とする正三角形を描くと、$\angle B=60^\circ$。$\angle B$について、角の二等分線を描くと、$\angle\text{ABP}=30^\circ$となる点Pを作図できる。
(1)図を参照
正三角形の1つの角の大きさは$60^\circ$であることを利用する。
辺ABを一つの辺とする正三角形を描くと、$\angle B=60^\circ$
$\angle B$について、角の二等分線を描くと、$\angle\text{ABP}=30^\circ$となる点Pを作図できる。
(2)
① $\sqrt{10} (\text{cm})$
点Aから辺CDにおろした垂線の足を点Eとする。$\triangle\text{AED}$において、三平方の定理より、
$AD^2 = AE^2 + ED^2 = 3^2 + 1^2 = 10$
$AD > 0$ なので、$AD = \sqrt{10}$
② $21\pi (\text{cm}^3)$
台形ABCD を、辺CD を軸として 1 回転させてできる立体は、底面の半径 3cm 高さ 2cm の円柱と、底面の半径 3cm 高さ 1cm の円錐である。
円柱の体積は、$(底面の半径)^2 \times \pi \times (高さ) = 3^2 \times \pi \times 2 = 18\pi (\text{cm}^3)$
円錐の体積は、$(底面の半径)^2 \times \pi \times (高さ) \times \frac{1}{3} = 3^2 \times \pi \times 1 \times \frac{1}{3} = 3\pi (\text{cm}^3)$
よって、求める立体の体積は、$18\pi (\text{cm}^3) + 3\pi (\text{cm}^3) = 21\pi (\text{cm}^3)$
(3)
$\triangle\text{ABF}$と$\triangle\text{DAG}$において、仮定より、
$\angle\text{BFA} = \angle\text{AGD} = 90^\circ \cdots\cdots$ ……①
$AB = DA \cdots\cdots$ ……②
$\angle\text{BAD} = 90^\circ$ より、
$\angle\text{BAF} = 90^\circ – \angle\text{DAG} \cdots\cdots$ ……③
$\triangle\text{DAG}$において、
$\angle\text{ADG} = 180^\circ – (90^\circ + \angle\text{DAG})$
$= 90^\circ – \angle\text{DAG} \cdots\cdots$ ……④
③④より、
$\angle\text{BAF} = \angle\text{ADG} \cdots\cdots$ ……⑤
① ②,⑤より、
直角三角形の斜辺と1つの鋭角がそれぞれ等しいから、
$\triangle\text{ABF} \equiv \triangle\text{DAG}$
次の1,2,3の問いに答えなさい。
(1)5人の生徒A,B,C,D,Eがいる。これらの生徒の中から、くじびきで2人を選ぶとき、Dが選ばれる確率を求めなさい。
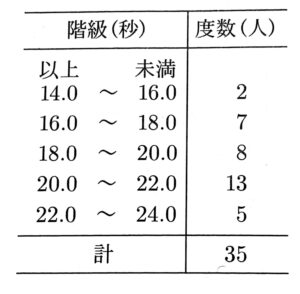
(2)次の表はあるクラスの生徒35人が水泳の授業で25mを泳ぎ、タイムを計測した結果を度数分布表にまとめたものである。
このとき、次の(1)(2)の問いに答えなさい。
① 18.0秒以上20.0秒未満の階級の累積度数を求めなさい。
② 度数分布表における、最頻値を求めなさい。
(3)次の図は、ある中学校の3年生100人を対象に20点満点の数学のテストを2回実施し、1回目と2回目の得点のデータの分布のようすをそれぞれ箱ひげ図にまとめたものである。
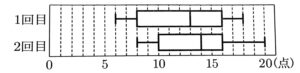
このとき、次の①②の問いに答えなさい。
① 箱ひげ図から読み取れることとして正しいことを述べているものを、次のア、イ、ウ、エの中から2つ選び、記号で答えなさい。
ア 中央値は、1回目よりも2回目の方が大きい。
イ 最大値は、1回目よりも2回目の方が小さい。
ウ 範囲は、1回目よりも2回目の方が大きい。
エ 四分位範囲は、1回目よりも2回目の方が小さい。
② 次の文章は、「1回目のテストで8点を取った生徒がいる」ことが正しいとは限らないことを説明したものである。【 】に当てはまる文を、特定の2人の生徒に着目して書きなさい。
箱ひげ図から、1回目の第一四分位数が8点であることがわかるが、8点を取った生徒がいない場合も考えられる。例えば、テストの得点を小さい順に並べたときに、【 】の場合も、第1四分位数が8点となるからである。
(1)選ばれる2人の組み合わせは、右図のとおり全部で 10 とおり
そのうち、生徒Dが選ばれるのは 4 とおりなので、確率は$\frac{4}{10}$
(2)
① 17(人)
18.0 秒以上 20.0 秒未満の階級の累積度数は、2+7+8=17(人)
② 21.0(秒)
最も度数の大きい階級は、20.0 秒以上 22.0 秒未満の階級である。最頻値は、この階級の中央値より、21.0(秒)
(3)
① ア、エ
ア…正しい
イ…最大値は、2回目の方が大きい
ウ…範囲は、1回目と2回目同じ
エ…正しい
② 25番目の生徒の得点が7点、26番目の生徒の得点が9点
100人のデータなので、第1四分位数は、テストの得点を小さい順に並べたときに25人目と26人目の得点の平均である。
次の1,2の問いに答えなさい。
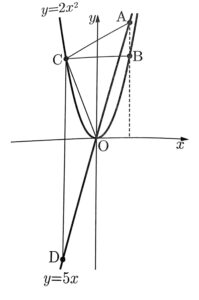
(1)次の図のように、2つの関数$y=5x,y=2x^2$のグラフ上で、x座標がt(t>0)である点をそれぞれA,Bとする。Bを通りx軸に平行な直線が、関数$y=2x^2$ぼグラフと交わる点のうち、Bと異なる点をCとする。また、Cを通りy軸に平行な直線が、関数$y=5x$のグラフと交わる点をDとする。
このとき、次の①②③の問いに答えなさい。
① 関数$y=2x^2$について、xの変域が-1≦x≦5のときのyの変域を求めなさい。
② t=2のとき、△OACの面積を求めなさい。
③ BC:CD=1:4となるとき、tの値を求めない、ただし、途中の計算も書くこと。
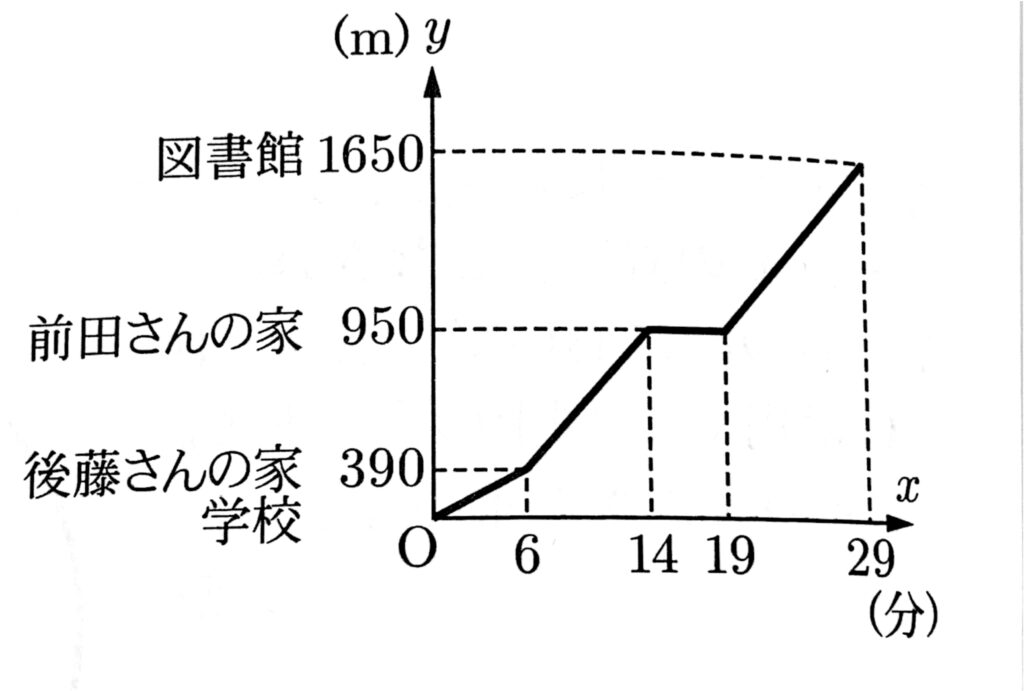
(2)ある日の放課後, 前田さんは友人の後藤さんと図書館に行くことにした。学校から図書館までの距離は1650mで、その間に後藤さんの家と前田さんの家がこの順に一直線の道沿いにある。
2人は一緒に学校を出て一定の速さで6分間歩いて、後藤さんの家に着いた。 後藤さんが家で準備をするため、2人はここで別れた。その、前田さんは毎分 70mの速さで8分間歩いて、自分の家に着き、家に着いてから5分後に毎分70mの速さで図書館に向かった。
(3)次の図は、前田さんが図書館に着くまでのようすについて、学校を出てからの時間をx分、学校からの距離をymとして、xとyの関係をグラフに表したものである。
このとき、次の①②③の問いに答えなさい。
① 2人が学校を出てから後藤さんの家に着くまでのxとyの関係を式で表しなさい。ただし、途中の計算も書くこと。
② 前田さんが後藤さんと別れてから自分の家に着くまでのxとyの関係を式で表しなさい。ただし、途中の計算も書くこと。
③ 後藤さんは準備を済ませ、自転車に乗って毎分210mの速さで図書館に向かい、図書館まで残り280mの地点で前田さんに追いついた。後藤さんが図書館に向かうために家を出たのは、家に着いてから何分何秒後か。
(1)
① $0 \le y \le 50$
$x$の変域が$-1 \le x \le 5$のとき、$y$の値は、$x=0$のとき最小値、$x=5$のとき最大値をとる。
$x=0$のとき、$y=2 \times 0^2 = 0$
$x=5$のとき、$y=2 \times 5^2 = 50$
よって、$y$の変域は、$0 \le y \le 50$
② 18
$t=2$のとき、各点の座標は、A(2,10), B(2,8), C(-2,8)となる。直線CAとy軸の交点をEとすると、Eのy座標は9となる。$\triangle\text{OAE}$と$\triangle\text{OCE}$の面積は、底辺をOE=9、高さを点Aのx座標2と考えると、
$\triangle\text{OAE} = 9 \times 2 \times \frac{1}{2} = 9$
$\triangle\text{OCE} = 9 \times 2 \times \frac{1}{2} = 9$
よって、$\triangle\text{OAC} = \triangle\text{OAE} + \triangle\text{OCE} = 9 + 9 = 18$
③ $t = \frac{3}{2}$
点Bのx座標はtなので、y座標は$2t^2$と表される。
また、点Dのx座標は$-t$なので、y座標は$5 \times (-t) = -5t$となる。
B(t, $2t^2$), C(-t, $2t^2$), D(-t, $-5t$)より、
BC = $2t$, CD = $2t^2 + 5t$ である。
BC : CD = 1 : 4 より
$4\text{BC} = \text{CD}$
$4 \times 2t = 2t^2 + 5t$
$2t^2 – 3t = 0$
$t(2t – 3) = 0$
$t=0, t=\frac{3}{2}$
$t > 0$ より $t = \frac{3}{2}$
この解は問題に適している。
よって、答えは $t = \frac{3}{2}$となる。
(2)
① (毎分)65(m)
(速さ) = (距離) ÷ (時間) なので、グラフより、390(m)÷6(分)=毎分 65m
② $y = 70x – 30$
グラフから、$(x, y)=(6, 390), (14, 950)$のいずれかを利用する。
グラフの傾きは速さと等しく、70 なので、$y=70x+b$ とおく。
$x$と$y$の関係の式は $y = 70x + b$ と表せる。
グラフは点(6, 390)を通るので
$390 = 70 \times 6 + b$
$b = -30$
したがって、求める式は $y = 70x – 30$
③ 14(分)20(秒後)
前田さんに追いついた地点は、図書館まで残り 280m なので、$y=1370$ である。
前田さんが家から図書館まで向かうときの $x$ と $y$ の関係式は、$y=70x+b$ に $(x, y)=(19, 950)$を代入して、$y=70x-380$ であることが分かる。
よって、後藤さんが前田さんに追いついたとき、$y=70x-380$ に $y=1370$ を代入して、$x=25$(分)である。
後藤さんが自分の家から前田さんに追いつくまでの $x$ と $y$ の関係式は、毎分 210m なので、$y=210x+b$ に $(x, y)=(25, 1370)$を代入して、$y=210x-3880$ である。
後藤さんの家は $y=390$ なので、上式に代入すると、$x = 20.3 = 20 + \frac{1}{3} = 20 + \frac{20}{60}$(分)
よって、後藤さんが家を出たのは20分20秒なので、家についてから14分20秒後となる。
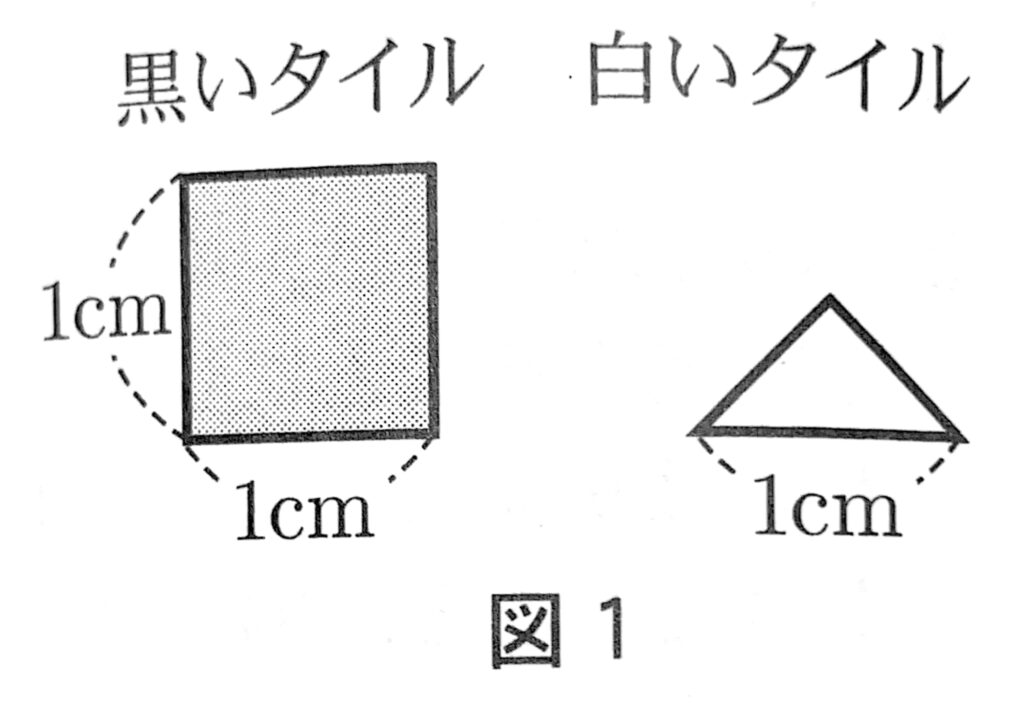
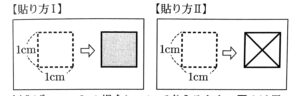
辺の長さがncm(nは2以上の整数)の正方形の板に、図1のような1辺の長さが1cmの正方形の黒いタイル、または斜辺の長さが1cmの直角二等辺三角形の白いタイルを貼る。板にタイルを貼るときは、黒いタイルを1枚使う【貼り方Ⅰ】、または白いタイルを4枚使う【貼り方Ⅱ】を用いて、タイルどうしが重ならないように板に隙間なくタイルをしきつめることとする。
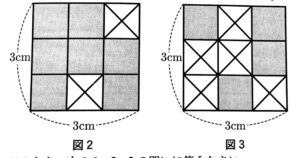
例えば、n=3の場合について考えるとき、図2は黒いタイルを7枚、知問いタイルを8枚、合計15枚のタイルを使って板にタイルをしきつめたようすを表しており、図3は黒いタイルを4枚、白いタイルを20枚、合計24枚のタイルを使って板にタイルをしきつめたようすを表している。
このとき、次の①②③の問いに答えなさい。
(1)n=4の場合について考える。白いタイルだけを使って板にタイルをしきつめたとき、使った白いタイルの枚数を求めなさい。
(2)n=5の場合について考える。黒いタイルと白いタイルを合計49枚使って板にタイルをしきつめたとき、使った黒いタイルと白いタイルの枚数をそれぞれ求めなさい。
(3)次の文章の①~③に当てはまる式や数をそれぞれ求めなさい。ただし、文章中のaは2以上の整数、bは1以上の整数とする。
n=αの場合について考える。 はじめに、黒いタイルと白いタイルを使って板にタイルをしきつめたとき,使った黒いタイルの枚数を6枚とすると, 使った白いタイルの枚数はaとb を用いて(①) 枚と表せる。
次に、この板の 【貼り方Ⅰ】 のところを【貼り方Ⅱ】に、【貼り方Ⅱ】 のところを【貼り方Ⅰ】に変更した新しい正方形の板を作った。 このときに使ったタイルの枚数の合計は, はじめに使ったタイルの枚数の合計よりも225枚少なくなった。 これを満たす a のうち,最も小さい値は ( ② ), その次に小さい値は(③)である。
(1)64(枚)
n=4のとき、1辺の長さが 1cm の正方形が 16 個である。
1辺の長さが 1cm の正方形には、白いタイルを4枚使うので、使った白いタイルの枚数は、 $16 \times 4 = 64$(枚)
(2)(黒いタイル)17(枚)、(白いタイル)32(枚)
黒いタイルをa枚、白いタイルをb枚使用するとする。
合計49枚使って板にタイルをしきつめるので、
$a+b=49 \cdots$ ……①
また、n=5のとき、1辺の長さが 1cm の正方形は 25 枚であり、この正方形に黒いタイルは1枚、白いタイルは4枚使うので、
$a + \frac{b}{4} = 25 \cdots $……②
①と②を連立して解くと、$a=17, b=32$
よって、黒いタイル17枚、白いタイル32枚
(3)① $4a^2 – 3b$ (枚) ② 9 ③ 11
①
n=aのとき、1辺の長さが 1cm の正方形は $a \times a = a^2$ (個)である。
黒いタイルをb枚使用すると、白いタイルを使用する正方形は、$a^2 – b$ (個)
白いタイルは1つの正方形に4枚使用するので、$4 \times (a^2 – b) = 4(a^2 – b)$ (枚)
②
①より、はじめに使ったタイルの枚数の合計は、$b + 4(a^2 – b) = 4a^2 – 3b$ (枚)である。
このとき、貼り方を変更すると、黒いタイルは、$a^2-b$ (枚)、白いタイルは、$4b$ (枚)となる。
よって、変更すると、タイルの枚数の合計は、$a^2 – b + 4b = a^2 + 3b$ (枚)である。
変更したとき、始めのタイルの枚数の合計より 225 枚小さくなるとき、
$4a^2 – 3b = a^2 + 3b + 225$
$3a^2 = 6b + 225$
$a^2 = 2b + 75$
bは1以上の整数なので、$a^2$は77以上の整数であり、奇数である。
b=3のとき、$a^2=81$であり、aは2以上の整数なので、$a=9$となり最も小さい値となる
③
b=23のとき、$a^2=121$であり、aは2以上の整数なので、$a=11$となり、次に小さい値となる
家庭教師のやる気アシストは、栃木県にお住まいの受験生のお子さんを毎年たくさん指導をさせ頂き、合格に導いています。
高い合格率の秘訣は、指導経験豊富な先生の指導力に加え、1対1の指導でお子さん一人ひとりの状況に合わせた、お子さんだけのカリキュラムで勉強が進められるから!
家庭教師のやる気アシストは、お子さんの志望校合格まで全力でサポートさせて頂きます!
お子さんにとって「成果が出る勉強法」ってどんな勉強法だと思いますか?
お子さんそれぞれに、個性や性格、学力の差もあります。そんな十人十色のお子さん全員に合う勉強法ってなかなかないんです。
たからこそ、受験生の今だけでもお子さんだけの勉強法で受験を乗り越えてみませんか?
やる気アシストには、決まったカリキュラムはありません。お子さんの希望や学力、得意や不得意に合わせて、お子さんだけのカリキュラムで指導を行っていきます。また、勉強法もお子さんそれぞれに合う合わないがあります。無料体験授業では、お子さんの性格や生活スタイルを見せていただき、お子さんにとって効率的な成果の出る勉強のやり方をご提案させて頂きます。

