前回は、新たに登場した連立方程式について説明しました。
今回は、その連立方程式を実際に活用して文章題を解いていきましょう！
方程式は、文章題で出てくることが多いので、実践問題に慣れておきましょう！

代金や速さ、割合などを題材にした問題について解説します。
解き方のコツを知って、周りと差をつけましょう！

実際に解く前に、連立方程式の文章題の特徴を整理しておきます。

1.連立方程式の文章題の特徴

特徴は2つです。

• 未知数（分からないもの）が 2つあり、それらを x,yとする
• 2つの式が必要である

1年生で習った方程式と大きく異なるのは、分からない数が2つ登場することです。
また、この解を導くには、2つの式が必要となります。
1つしか式が作れていない場合、解を求めることができません。
この特徴を理解したうえで解いてみましょう！

つまり、下に示したような順番で解くことが大切です。

連立方程式の文章題の解き方

1. 未知数2つは何か明確にして、ｘ,ｙとする
2. その未知数を含む式を2つつくる

 この順番で解いていきましょう！

 ほかにも、文章題を解く上でのポイントを先にまとめておきます！

連立方程式の文章題を解くポイント

• 問題文の本質を理解して言い換える！
• 速さの問題は図を書く！
• 何をｘ,ｙで置いたか、単位を含めてメモしておく！

 では実際の問題を解いていきましょう！

2.文章題　人数と代金

まずは、人数と代金に関する文章題です。
日常的に考えるような内容なので、分かりやすいはずです！

例題1

遊園地の入場料は、大人4人と子供2人では24,000円、大人3人と子供4人では25,500円になる。
大人1人と子供1人の入場料はそれぞれいくらか。

解答1

大人1人の入場料：4500円
子供1人の入場料：3000円

解説1

先ほど説明した以下の順番で解いていきましょう。

1. 未知数2つは何か明確にして、ｘ,ｙとする
2. その未知数を含む式を2つつくる

1.未知数2つは何か明確にして、ｘ,ｙとする
この問題における未知数2つとは、求めたいものと同じです。
つまり、未知数は「大人1人の入場料」と「子供の1人の入場料」です。
そこで、「大人1人の入場料」をｘ円、「子供の1人の入場料」をｙ円とします。

2.その未知数を含む式を2つつくる
では、次に式を作っていきましょう。
 文章をよく読み、未知数の関係から式を作ります。
「大人4人と子供2人では24,000円」から1つ目の式ができ、
「大人3人と子供4人では25,500円」から2つ目の式ができます。

まず、「大人4人と子供2人では24,000円」から1つ目の式を作ります。
これを未知数を使って日本語で表現すると、
「大人1人ｘ円の入場料を4人分と、子供1人ｙ円の入場料を2人分払うと、24,000円」
ということです。
これを式で表すと、
ｘ（大人1人の入場料）×4（大人の人数）＋ｙ（子供1人の入場料）×2（子供の人数）＝24,000（入場料合計）
したがって、
4ｘ＋2ｙ＝24000　　…①
次に、同様に「大人3人と子供4人では25,500円」から2つ目の式を作ると、
3ｘ＋4ｙ＝25500　　…②

①，②の2つの式ができたので、これらを解いていきます。
係数をそろえるため、①を2倍して引き算します。
①×2－②をします。

　　8ｘ＋4ｙ＝48000
ー）3ｘ＋4ｙ＝25500
　　5ｘ　　   ＝22500
したがって、ｘ＝4500

①の式に代入してｙも求めます。
18000＋2ｙ＝24000
2ｙ＝6000
ｙ＝3000

これで、大人子供共に両方の入場料が分かりましたね！
答えは、

• 大人1人の入場料：4500円
• 子供1人の入場料：3000円

となります。

3．文章題　個数と代金

先程に比べて、日常らしさは減りますが、これもよく出る問題です。
未知数が分からない数・求めたい数であることを覚えておけば大丈夫です！

例題2

財布の中に、10円玉と50円玉が合わせて30枚、合計620円分あった。
このとき、10円玉と50円玉はそれぞれ何枚あったか求めなさい。

解答2

10円玉は8枚
50円玉は22枚

解説2

では先ほどの問題と同様に解いていきましょう。

1.未知数2つは何か明確にして、ｘ,ｙとする
この問題における未知数2つとは、「10円玉の枚数」と「50円玉の枚数」です。
そこで、「10円玉の枚数」をｘ枚、「50円玉の枚数」をｙ枚とします。

2.その未知数を含む式を2つつくる
では、次に式を作っていきましょう。
文章題のどの部分から式が出来ると思いますか？
「10円玉と50円玉が合わせて30枚」から1つ目の式ができ、
「（10円玉と50円玉が合わせて）合計620円分」から2つ目の式ができます。

「10円玉と50円玉が合わせて30枚」からは、
ｘ＋ｙ＝30　　…①

「（10円玉と50円玉が合わせて）合計620円分」からは、
10ｘ＋50ｙ＝620 　　…②

この①と②の二式を解くと、未知数を求めることができます。
前回の問題と同様に係数を揃えます。
この際、①をそのまま10倍してもいいのですが、簡単に解く方法があるので紹介します！

簡単に計算するコツ！ 係数を同じ数で割る
具体的に②を簡単にしてみましょう。
係数がすべて10の倍数ですよね？
そこで、全ての係数を10で割ります。
すると、とても簡単な数字で式を表すことができます。
10ｘ＋50ｙ＝620 　　…②
　　　⇓÷10
ｘ＋5ｙ＝62　　　　…②’

よって、①と②’を連立して解くと、
　　ｘ＋5ｙ＝62
ー）ｘ＋ｙ＝30
　　　4ｙ＝32
したがって、ｙ＝8

②’より、
ｘ＋5×8＝62
ｘ＝22

以上から、
10円玉は8枚、50円玉は22枚あったことが分かります。

4．文章題　速さ①

これは苦手な人が多い文章題です。
丁寧に解説するので、この機会に完璧にしましょう！
ポイントは、情報を図に落とし込んで整理することです！

例題3

家から学校への道のり1.2kmを、はじめは分速60mの速さで歩いた。
ところが途中で、遅刻するのが怖くなり、分速80mの小走りで学校に向かった。
すると合計で18分かかった。
このとき何分歩いて、何分小走りだったでしょうか。

解答3

12分歩いて、6分小走りだった

解説3

では先ほどの問題と同様に解いていきましょう。

1.未知数2つは何か明確にして、ｘ,ｙとする
この問題における未知数2つとは、「歩いた分数」と「小走りした分数」です。
そこで、「歩いた分数」をｘ分、「小走りした分数」をｙ分とします。

2.その未知数を含む式を2つつくる
では、次に式を作っていきましょう。
文章題のどの部分から式が出来ると思いますか？
「合計で18分かかった」から1つ目の式ができ、
「家から学校への道のり1.2km」から2つ目の式ができます。
この2つ目の式がなかなか作れない方が多いです。

そこで情報を整理するのがポイントです。
文章題を数直線にまとめると、下図のようになります。
この時、必ず単位をしっかり書きましょう！

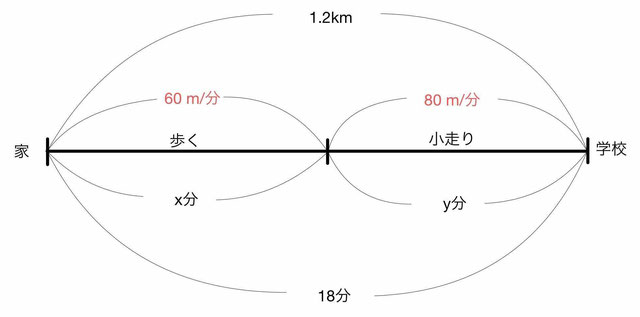
1つ目の式は、「合計で18分かかった」から、時間に関する式ができます。
「歩いた時間と小走りした時間を合計すると18分だった」という意味なので、
ｘ＋ｙ＝18　　…①

2つ目の式は、「家から学校への道のり1.2km」から、距離に関する式ができます。
「歩いた距離と小走りした距離を合計すると1.2㎞（1200ｍ）だった」という意味なので、
歩いた距離＝分速60m  ×  ｘ分
小走りした距離＝分速80m  ×  ｙ分
より、
60ｘ＋80ｙ＝1200　　…②

単位を統一することを忘れないようにしましょう！
今回の場合は、1.2kmを「ｍ」に直す必要があります。

前回の問題と同様に、係数を同じ数で割ることで簡単な数字に直しましょう。
今回は、20で割ると良さそうですね。
したがって、②を変形して
3ｘ＋4ｙ＝60　　…②’

では、二式を連立して解きましょう。
係数をそろえるため、①に３をかけましょう。
②’－①×３で、
　　3ｘ＋4ｙ＝60
ー）3ｘ＋3ｙ＝54
　　　　　 ｙ＝6

①にｙ＝6を代入すると、
ｘ＋6＝18
ｘ＝12

したがって、12分歩いて、6分小走りだったということが分かります。

＼小・中・高校生の勉強にお悩みのある方へ／

5.文章題 速さ②

もうひとつよく出る速さに関する問題を紹介します。
これは慣れていないと、文章の意味が読み取りにくいため、なかなか解くことが出来ません。
そこで、あらかじめ練習しておき、周囲と差をつけましょう！
ポイントは、文章題の問題文の本質を理解し、言い換えることです！

例題4

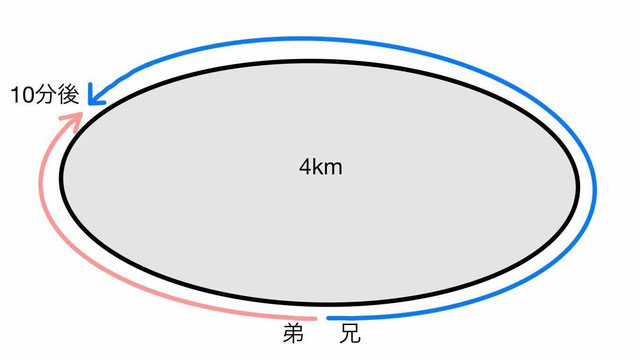
兄と弟が1周4kmのランニングコースにいきます。
兄は自転車で、弟はジョギングで回ります。
兄弟が逆の方向に出発すると10分後に出会い、
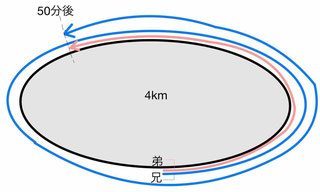
同じ方向に出発すると50分後に兄は1周してから、弟に追いつきます。
このとき、兄と弟の速さはどれくらいですか？

解答4

兄は分速240m
弟は分速160m

解説4

では先ほどの問題と同様に解いていきましょう。

1.未知数2つは何か明確にして、ｘ,ｙとする
この問題における未知数2つとは、「兄の速さ」と「弟の速さ」です。
いつもと異なるのは、単位に気を付けることです！
速さを表現する際は、「分速」や「秒速」、「m」や「km」などの単位を明確にする必要があります！
今回は、文章の単位にしたがい、「分速」と「m」を使用しましょう。
そこで、「兄の速さ」を分速ｘm、「弟の速さ」を分速ｙmとします。

2.その未知数を含む式を2つつくる
では、次に式を作っていきましょう。
文章題のどの部分から式が出来ると思いますか？
「1周4kmのランニングコース、兄弟が逆の方向に出発すると10分後に出会う」から1つ目の式ができ、
「1周4kmのランニングコース、同じ方向に出発すると50分後に兄は1周してから、弟に追いつく」から2つ目の式ができます。
分かりましたか？
これはなんとなく分かっても、どうやって式を立ててよいのか分からない方が多いと思います！
順番に見ていきましょう！

では、最後に二式を連立して解きましょう。
その前に、今回も係数を簡単な数字に直せるので直しましょう。
①÷10より、
ｘ＋ｙ＝400　　…①’
②÷50より、
ｘ－ｙ＝80　　   …②’

①’＋②’より、
2ｘ＝480

ｘ＝240

①’にｘ＝240を代入すると、
240＋ｙ＝400
ｙ＝160

したがって、兄は分速240mで、弟は分速160mだとわかります。

6.文章題　割合

例題5

ある学校の去年の生徒数は、男女合わせて600人だった。
今年は去年に比べ、男子が10％減って、女子は20％増えた。
その結果、全体で615人になった。
今年の男子、女子の生徒数を求めなさい。

解答5

今年の男子　315人
今年の女子　300人　

解説5

では同様に解いていきましょう。

1.未知数2つは何か明確にして、ｘ,ｙとする
この問題における求めたい数は、「今年」の男女の人数です。
しかし、今年の人数をｘ,ｙとすると、あとの計算がとても難しくなってしまいます。

そこで、「去年」の人数をｘ,ｙとして、去年の人数を求めた後に今年の人数を求めるという解法で求めましょう！
つまり、「去年の男子の人数」をｘ人、「去年の女子の人数」をｙ人とします。

2.その未知数を含む式を2つつくる
では、次に式を作っていきましょう。
文章題のどの部分から式が出来ると思いますか？
「去年の生徒数は、男女合わせて600人だった」から1つ目の式ができ、
「今年は去年に比べ、男子が10％減って、女子は20％増えた。その結果、全体で615人になった。」から2つ目の式ができます。

まず、1つ目の式を作ります。
「去年の生徒数は、男女合わせて600人だった」から、
ｘ＋ｙ＝600　　…①

では次に、2つ目の式を作ります。
「今年は去年に比べ、男子が10％減って、女子は20％増えた。その結果、全体で615人になった」より、

今年の男子の人数は、去年の男子の90％
今年の女子の人数は、去年の女子の120％であるから、

0.9ｘ＋1.2ｙ＝615　　…②

では、二式を連立して解きましょう。
その前に、今回も係数を簡単な数字に直せるので直しましょう。

②×10より、
9ｘ＋12ｙ＝6150　　   …②’

②’ー①×9より、
　　9ｘ＋12ｙ＝6150
ー）9ｘ＋9ｙ＝5400
　　　　　3ｙ＝750
したがって、ｙ＝250

①にｙ＝250を代入すると、
ｘ＋250＝600
ｘ＝350

したがって、去年の男子は350人、女子は250人だとわかります。
これを今年の人数に直していきましょう！
この工程を忘れてしまわないように注意しましょう！
今年の男子：350×0.9＝315
今年の女子：250×1.2＝300

連立方程式を利用した文章題を4つ紹介しました。
これらを解けるようにすれば、他の問題もきっと解けるはずです！
まずはこれらをマスターしましょう！