【数学】一次関数の利用
グラフ、図形、色々な分野が登場する一次関数の応用問題。
この記事では定期テストで差がつく一次関数の利用について、頻出問題とともに徹底解説します！
もし一次関数の基本が不安という方は、基礎から解説した別の記事があるのでそこから復習にお役立てください！
目次
1.一次関数と連立方程式➀
一次関数の応用のひとつに、連立方程式があります。
連立方程式とは、下のように二つ以上の式が組み合わさっている式の事です。
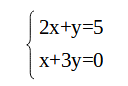
前回の単元で勉強をしましたね。加減法や代入法を勉強したのを覚えていますか？不安な方は復習をしておきましょう。
実は今回教えたい事は、この連立方程式がなんと一次関数で求めることができるということです！
では早速、例題を解きながら一緒に勉強していきましょう。
そのためにまずそれぞれの式をグラフに表せる形に変形する必要があります。
つまり y=ax+b の形を目指します。実際に一次関数のグラフを書いてみましょう。
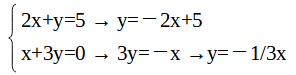
変形ができたら、グラフを書いていきます。
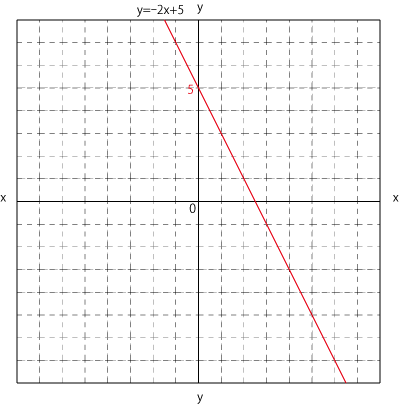
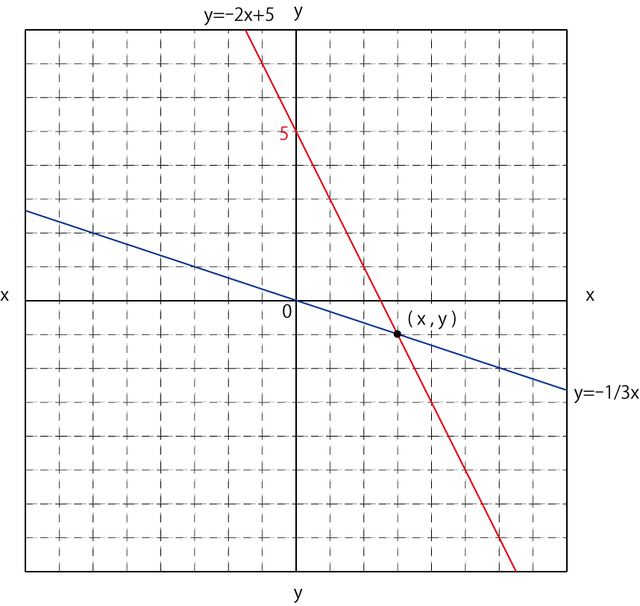
グラフを書いてみると、交点があることがわかります。
この交点のx座標とy座標が答えになります。
よって、グラフから読みとって連立方程式の解は（x,y）= (3,-1) となります。
２．一次関数と連立方程式②
ここまでは、式からグラフを導く方法を勉強しました。
次の例題では、グラフから式を導いていきます。
先ほどと逆のことをしている、ということを意識して見ていきましょう。
（問）次の図の2直線の交点の座標を求めなさい。
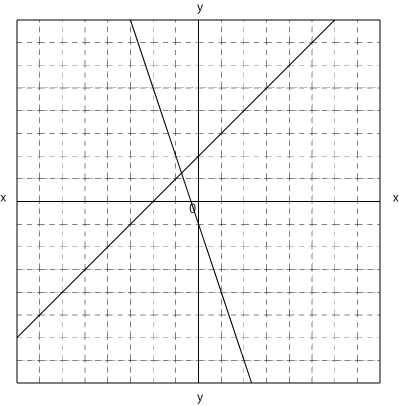
一見何の情報も内容に見えるこのグラフですが、切片に注目してください。
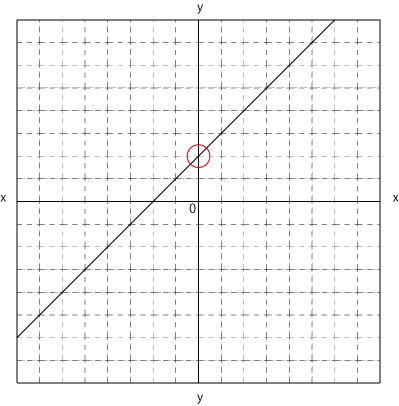
まずこのグラフに焦点を当てると、切片が２であることが分かり、続いて
傾きが１であることも読み取れます。
今分かったことをy=ax+b にあてはまると、y=x+2 になります。
同じ要領でもうひとつのグラフも考えていきましょう。
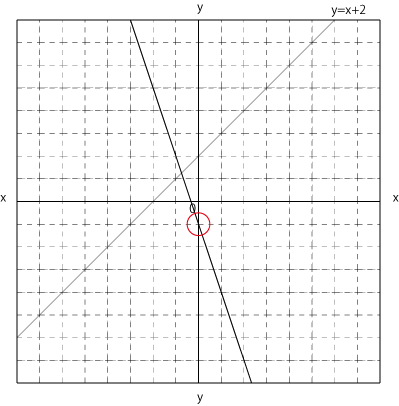
グラフから切片-1，傾き-3であることがわかり、y=-3x-1 がグラフの式であることが分かります。
式が分かったので、連立方程式にして解を求めていきます。
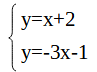
今回は代入法で求めます。
→x+2=-3x-1 となり x=-3/4 。xの値を代入して、y=-3/4+2 (もしくはy=-3×-3/4-1)
→y=5/4 となります。
＼小・中・高校生の勉強にお悩みのあるお子さん・保護者様へ／
＼小・中・高校生の勉強にお悩みのある方へ／
3. 一次関数と軸の交点
ここまで、グラフを使った問題を考えてきました。グラフのいいところは、イメージがしやすいという点です。
次の問題も文章だけだとイメージがしづらいです。積極的にグラフを書いて考えていきましょう。
（問）y=2x-5がx軸と点Aで交わっている。点Aの座標を求めなさい。
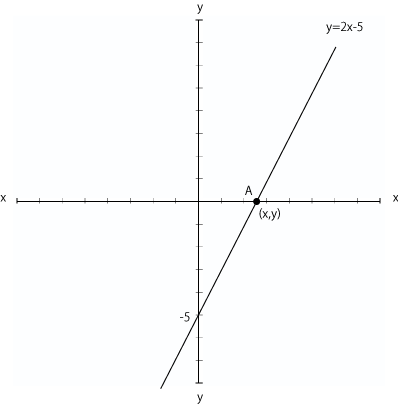
簡易的に図を描いてみました。
実際に紙に図を描くとこんなに綺麗には書けませんが、先ほど述べたように
イメージすることが大切です。
点Aの座標はまだ分かっていないので（x,y）としました。
問題文の「x軸と交わっている」ということをグラフを見て考えてみると
ｙの値が０であることが分かります。
つまり（x,0）になります。
座標のｙの値が分かったので、式のyに当てはめていきましょう。
0=2x-5 →5=2x →x=5/2 よって（x,y）=（5/2,0）
（別解）この問題は、連立方程式を用いて求めることもできます。
ｘ軸をy=0という式として考えて、
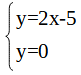
という連立方程式を作って解いても同じ答えになります。
４．図形を動く点と面積
一次関数の典型的な応用問題です。 １つ１つ丁寧に考えていきましょう。
問）図の長方形ABCDで、点PはAを出発して、辺上をB、Cを通りDまで行く。
点PがAからｘcm動いたときの△APDの面積をy㎠として、次の問いに答えなさい。
①点Pが辺ABを動くときのyをxで表しなさい。
②点Pが辺CDを動くときのyをxで表しなさい。
③点Pが辺AB,BC,CD上を動くときの
△APDの面積の変化の様子を表すグラフを書きなさい。
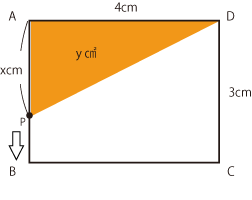
➀ 辺ADを底辺として考えましょう。点PがAB上を動くということは、
三角形の高さが変化するということです。
三角形の面積を求める底辺×高さ×1/2に当てはめて、
ｙ（面積）＝ 4×ｘ×1/2 よって ｙ＝２ｘが答えになりなす。
② 点PはAからB、Cを通りDに行く。このうちCからDの部分だけを限定するにはどうすればよいでしょうか。
この問題では、図のようにAPの長さをｘ㎝としています。そして辺ＡＤを除く長方形の長さは10㎝です。
つまり、点Pが辺CDを動くときPDの長さは10-x ㎝と表せます。
後は➀と同様に考えて、ｙ＝４×（10-ｘ）×1/2
よって ｙ＝-2ｘ+20 が答えになります。
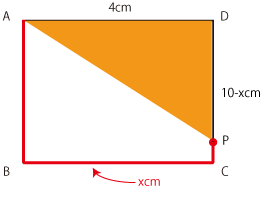
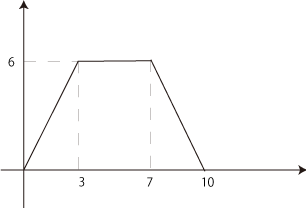
③ 点PがAからBに向かうまでは面積が増加、CからDに向かうと面積が減少することが
➀と②から推察できるかと思います。また、点PがBからCを移動するときは三角形の高さが変わらないので面積は変わらないことにも気づいたでしょうか。
以上の情報と①、②の答えをグラフにするとこのようになります。
＼小・中・高校生の勉強にお悩みのあるお子さん・保護者様へ／
＼小・中・高校生の勉強にお悩みのある方へ／
５．一次関数とダイヤグラム
この問題は、グラフを理解することが重要になります。
一見何のことか分からないですが、グラフの単位や数字をヒントにして考えましょう。
（問）下の図は8km離れているA駅とB駅の間の、９時から１０時までの電車の運行を表したグラフである。次の問いに答えなさい。
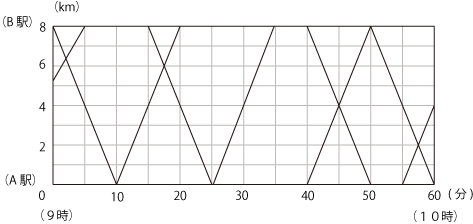
➀ B駅を９時４０分に出発いた電車が、A駅から来る電車に出会う時刻を求めよ。
② サトシ君はA駅を９時５分に出発して、時速１２㎞の自転車で線路沿いの道をB駅まで行った。
サトシ君はB駅に着くまでに電車と何回出会ったか。グラフを書いて答えなさい。
➀ この問題はダイヤグラムから読み取れる問題です。ちなみに、ダイヤグラムとは
今回でいう電車の運行を表したグラフのことです。
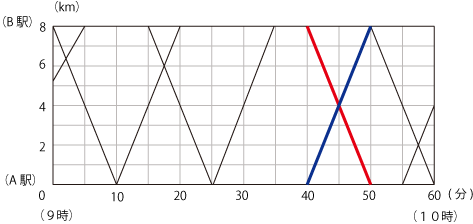
赤く強調した部分が９時４０分にB駅を出発した電車です。
そして青く強調した部分が９時４０分にA駅を出発した電車です。
２つのグラフの重なっている点が電車が出会った点になります。
下の目盛を参考にして、９時４５分が答えになります。
② ダイヤグラムから、A駅からB駅までの距離が８㎞であることが分かります。そして問題文からサトシ君の速さも時速１２ｋｍと分かっています。
以上からハジキの計算で時間を求めることができます。
８（㎞）÷１２＝2/3（時間） →2/3時間を分単位に直して４０分となります。（60×2/3）
ここまで分かれば、サトシ君のグラフのを書くことができます。
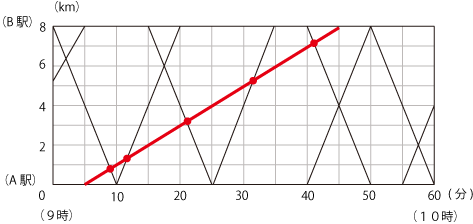
グラフと交わっている回数が、電車と出会った回数になります。
よって6回が答えになります。
この記事を書いた人
趣味：カメラ
これまで学習アドバイザーとして沢山のお子さんのお悩みを解決してきました。そのノウハウや勉強のコツなどをこの記事を通して発信していきます。
Instagram・ⅹなどでも情報発信中ですので、ぜひフォローください！
